Vectors, Chapter Notes, Class 12, Maths (IIT) PDF Download
Basic Concepts of Vectors - Vector Algebra, Class 12, Maths
F. LINEAR COMBINATIONS
Given a finite set of vectors then the vector
is called a linear combination of
We have the following results :
Ex.18 Show that the points whose position vectors are are collinear.
Sol. Let the given points be A, B, C and O be the point of reference.
Hence the condition of collinearly (i) and (ii) are satisfied. Hence the given points are collinear.
Ex.19 Examine if are linearly independent or dependent.
Sol.
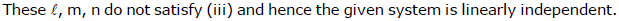
G. VECTOR PRODUCT OF TWO VECTORS
Vector quantities are of frequent occurrence, which depend each upon two other vector quantities in such a way as to be jointly proportional to their magnitudes and to the sine of their mutual inclination, and to have a direction perpendicular to each of them. We are therefore led to adopt the following
Definition : The vector product of two vectors whose directions are inclined at an angle θ, is the vector whose modulus is ab sin θ, and whose direction is perpendicular to both
being positive relative to a rotation from
where nˆ is a unit vector perpendicular to the plane of having the same direction as the translation of a right-handed screw due to a rotation from
From this it follows that
has the opposite direction to
The order of the factors in vector product is not commutative; for a reversal of the order alters the
sign of the product.
Consider the parallelogram OAPB whose sides OA, OB have the lengths and directions of respectively. The area of the figure is ab sin θ, and the vector area OAPB, whose boundary is described in this sense, is represented by
This simple geometrical relation will be formed useful. The vector area OBPA is of course represented by b × a.
For two parallel vectors sin θ is zero and their vector product vanishes. The relation a × b = 0 is thus the condition of parallelism of two proper vectors. In particular, r × r = 0 is true for all vectors. If, however, a is a vector whose modulus is ab, and whose direction is such that
form a right-handed system of mutually perpendicular vectors. If
are both unit vectors the modulus of
is the sine of their angle of inclination. For the particular unit
These relations will be constantly employed.
If either factor is multiplied by a number, their product is multiplied by that number. For
Distributive Law : We shall now show that the distributive law holds for vector products also ;
From the distributive law may be deduced a very useful formula for the vector product
in terms of rectangular components of the vectors. For, with the usual notation,
in virtue of the relation proved in the preceding Art. We may write this in the determinantal form
This vector has modulus ab sin θ. Hence, on squaring both members of the above equation and dividing
by a2b2, we find for the sine of the angle between two vectors
Remark :
Vector area : Consider the type of vector quantity whose magnitude is an area. Such a quantity is associated with each plane figure, the magnitude being the area of the figure, and the direction that of the normal to the plane of the figure. This vector area therefore specifies both the areaand the orientation of the plane figure. But as the direction might be either of two opposite directions along the normal, some convection is necessary. The area clearly has no sign in itself, and can be regarded as positive or negative only with reference to the direction in which the boundary of the figure is described, or the side of the plane from which it is viewed.
Consider the area of the figure bounded by the closed curve LMN, which is regarded being traced out in the direction of the arrows, the normal vector , bears to this direction of rotation the same relation as the translation to the direction of rotation of a right-handed screw. The area LMN is regarded as positive relative to the direction of
. With this convention a vector area may be represented by a vector normal to the plane of the figure, in the direction relative to which it is positive, and with modulus equal to the measure of the area. The sum of two vector areas represented by
is defined to be the vector area represented by
Ex.20 uˆ and vˆ are two non-colinear unit vectors such that
Sol.
Ex.21 Let Am be the minimum area of the triangle whose vertices are A(–1, 1, 2); B(1, 2, 3) and C(t, 1, 1) where t is a real number. Compute the value of
Sol.
H. SHORTEST DISTANCE BETWEEN TWO LINES
If two lines in space intersect at a point, then obviously the shortest distance between them is zero.
Lines which do not intersect & are also not parallel are called skew lines. For Skew lines the direction of the shortest distance would be perpendicular to both the lines. The magnitude of the shortest distance vector would be equal to that of the projection of along the direction of the line of shortest distance,
I. PRODUCT OF THREE VECTORS
(a) SCALAR TRIPLE PRODUCT : Scalar triple product, Since the cross product
is itself a vector, we may form with it and a third vector
the scalar product
which is a number. Such products of three vectors are of frequent occurrence, and we shall find it useful to examine their properties. Consider the parallelopied whose concurrent edges OA, OB, OC have the lengths and directions of the vectors
respectively. Then the vector
which we may denote by
is perpendicular to the face OBDC, and its modulus n is the measure of the area of that face. If θ is the angle between the directions of
the triple product
where V is the measure of the volume of the parallelepiped. The triple product is positive if θ is acute, that is if form a right-handed system of vectors.
The same reasoning shows that each of the products has the same value ± V, being positive if the system
is right handed, negative if left-haded. The cyclic order
is maintained in each of these. If, however that order is changed, the sign of the product is
Thus the value of the product depends on the cyclic order of the factors, but is indpendent of the
position of the dot and cross. These may be interchanged at pleasure. It is usual to denote the above
I


Ex.22 If are three mutually perpendicular unit vectors, prove that
are also mutually perpendicular unit vectors.
Sol. Let the three given unit vectors be Since they are mutually perpendicular
Ex.23 If V be the volume of a tetrahedron & V' be the volume of the tetrahedron formed by the centroids then find the ratio of V & V'
FAQs on Vectors, Chapter Notes, Class 12, Maths (IIT)
| 1. What are vectors and how are they used in mathematics? |  |
| 2. How are vectors represented and manipulated in mathematics? |  |
| 3. What are some real-life applications of vectors? |  |
| 4. How can vectors be used to solve geometric problems? |  |
| 5. Can vectors be used to solve optimization problems? |  |

















