Vectors | Physics for EmSAT Achieve PDF Download
| Table of contents |

|
| Introduction |

|
| Vector algebra |

|
| Products of vectors |

|
| Coordinate systems |

|
| Calculus of vectors |

|
Introduction
Vector analysis is a mathematical discipline concerned with quantities that possess both magnitude and direction. In the realm of physics and geometry, certain quantities, referred to as scalars, can be completely described by their magnitude using appropriate units of measurement. For instance, mass can be expressed in grams, temperature in degrees on a specific scale, and time in seconds. Scalars can be visually represented by points on a numerical scale, such as a clock or thermometer. On the other hand, there exist quantities known as vectors, which necessitate the specification of both magnitude and direction. Velocity, force, and displacement are examples of vector quantities. A vector quantity can be graphically depicted by a directed line segment, denoted by an arrow pointing in the direction of the vector, with the length of the segment representing the magnitude of the vector.
Vector algebra
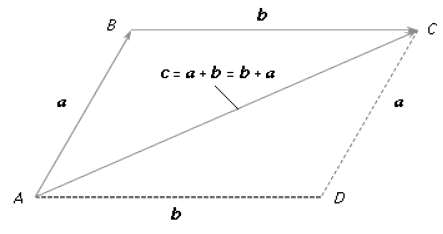
- In vector analysis, a prototype vector is represented by a directed line segment AB (refer to Figure 1). This line segment can be visualized as the displacement of a particle from an initial position A to a new position B. To differentiate vectors from scalars, it is common practice to represent vectors using boldface letters. Hence, in Figure 1, the vector AB can be denoted as vector a, and its length or magnitude is represented by |a|. In many scenarios, the specific location of the initial point of a vector is irrelevant. As a result, two vectors are considered equal if they possess the same length and direction.
- The equality between two vectors, denoted as a = b, is expressed through standard symbolic notation. Geometry provides helpful definitions for the fundamental algebraic operations involving vectors. For instance, in Figure 1, if the displacement from point A to point B is represented by AB = a, and subsequently, the particle is moved to point C, resulting in BC = b, it becomes evident that the overall displacement from A to C can be achieved by a single displacement represented by AC = c. Hence, it is reasonable to state a + b = c.
- This method of constructing the sum, c, of vectors a and b produces the same outcome as the parallelogram law, where the resultant vector c corresponds to the diagonal AC of the parallelogram formed using vectors AB and AD as its sides. As the initial point B of vector BC = b is inconsequential, it follows that BC = AD. In Figure 1, AD + DC = AC, thereby satisfying the commutative law.
a + b = b + a (1) - The commutative law, expressed as a + b = c, applies to vector addition. Furthermore, it can be demonstrated that the associative law, shown in the equation, remains valid. Therefore, parentheses in equation (2) can be omitted without introducing any ambiguities.
(a + b) + c = a + (b + c) (2) - When a scalar, represented by the variable s, is multiplied by a vector a, denoted as sa or as, the resulting vector has a length of |s||a| and follows the direction of a when s is positive. However, if s is negative, the resulting vector points in the opposite direction of a. Hence, vectors a and -a possess equal magnitudes but opposite directions. Based on these definitions and the familiar properties of scalar numbers (represented by s and t), the equations hold true.

- The fact that laws (1), (2), and (3) are identical to those encountered in ordinary algebra enables the application of familiar algebraic rules to solve systems of linear equations involving vectors. This correspondence allows for the deduction of theorems in synthetic Euclidean geometry, which often require complex geometric constructions, through purely algebraic methods.
Products of vectors
The multiplication of vectors leads to two types of products, the dot product and the cross product.
- The dot product, or scalar product, of two vectors a and b is denoted as a·b and represents a real number |a||b| cos (a,b), where (a,b) denotes the angle between the directions of vectors a and b. Geometrically, this relationship can be expressed as the equation.

- When vectors a and b are perpendicular (at right angles), their dot product a·b equals zero. If neither vector a nor vector b is a zero vector, the dot product being zero indicates that the vectors are perpendicular. When vector a is equal to vector b, the angle between them (a,b) is cos (a,b) = 1, and the dot product a·a = |a|² provides the square of the length of vector a.

- The dot multiplication of vectors adheres to the associative, commutative, and distributive laws of elementary algebra.
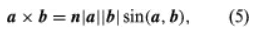
- Let n be a vector with a unit length, perpendicular to the plane formed by vectors a and b. The direction of n is such that if a right-handed screw is rotated from vector a towards vector b, it will advance in the direction of n (refer to Figure 2). When vectors a and b are parallel, their cross product a × b equals zero. The magnitude of the cross product a × b can be represented by the area of the parallelogram formed by vectors a and b as adjacent sides. Additionally, as the rotation from vector b to vector a is opposite to the rotation from vector a to vector b, the equation illustrates this relationship.
a x b = -b x a - This demonstrates that the cross product is not commutative; however, the associative law (sa) × b = s(a × b) and the distributive law, expressed in the equation, are valid for cross products.
a x (b + c) = a x b + a x c (6)
Coordinate systems
Vector analysis serves as an ideal tool for studying the physical universe because empirical laws of physics are independent of reference frames chosen to represent physical relationships and geometric configurations. By introducing a special reference frame or coordinate system, a correspondence is established between vectors and sets of numbers that represent the vector components in that frame. This leads to defined rules of operation on these number sets, which follow from the rules for operations on line segments.
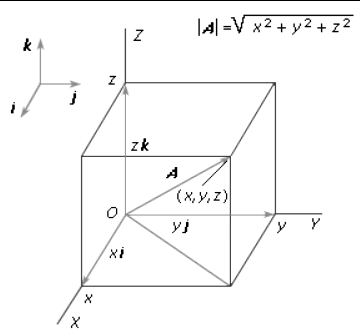
By selecting a specific set of three noncollinear vectors, known as base vectors, any vector A can be uniquely expressed as the diagonal of a parallelepiped formed by the components of A in the directions of the base vectors. The commonly used set consists of three mutually orthogonal unit vectors, denoted as i, j, and k, aligned with the axes of the Cartesian reference frame.
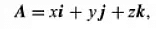
In this system, the expression takes the form of the equation, where x, y, and z represent the projections of A onto the coordinate axes.
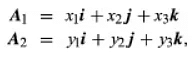
When two vectors A1 and A2 are represented as given in the equations, their sum can be determined using the laws mentioned, resulting in the equation for their sum.
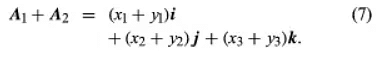
In a Cartesian frame, the sum of A1 and A2 is the vector determined by the coefficients (x1 + y1, x2 + y2, x3 + y3).
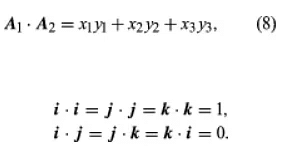
The dot product can also be expressed using the equation, as shown, since it follows from the equations provided. The cross product, obtained using law (6), is the vector determined by the triple of coefficients of i, j, and k in equation (9).
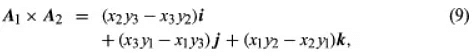
Using 1 × 3 (or 3 × 1) matrices to represent vectors with components (x1, x2, x3), formulas (7) through (9) can be rephrased in the language of matrices. This allows for the generalization of the concept of a vector to spaces of higher dimensions beyond three. For example, the state of a gas may depend on four parameters: pressure (p), volume (v), temperature (T), and time (t). This quadruple of numbers cannot be represented by a point in a three-dimensional reference frame. However, by introducing a four-dimensional reference frame defined by the base vectors a1, a2, a3, and a4 with components

determined by the rows of the matrix provided, the vector x can be represented x = x1a1 + x2a2 + x3a3 + x4a4 by the quadruple of components (x1, x2, x3, x4) in a four-dimensional space.
Calculus of vectors
A particle moving in three-dimensional space can be located at any given time t using a position vector r originating from a fixed reference point O. Since the position of the terminal point of r depends on time, r is a vector function of t. Its components in the directions of the Cartesian axes at point O are the coefficients of i, j, and k in the representation equation.
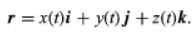
If these components are differentiable functions, the derivative of r with respect to t gives the velocity v of the particle, with its Cartesian components appearing as coefficients of i, j, and k in equation (10). If these components are also differentiable, the acceleration a = dv/dt can be obtained by differentiating equation (10) to find the equation.
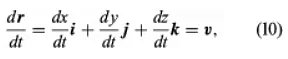
The rules for differentiating products of scalar functions remain valid for derivatives of dot and cross products of vector functions. Suitable definitions of integrals of vector functions allow the development of the calculus of vectors, which has become a fundamental analytical tool in physical sciences and technology.

|
212 videos|286 docs|193 tests
|















