Volume Of Prisms & Cylinders
The volume of a solid is the amount of space inside the object. It's how much water fits inside a bathtub, how much sand fills a bucket, or how much soda your friend can chug and hold in his stomach.
Take a look at this rectangular prism. The volume is the number of unit blocks that fill the prism.
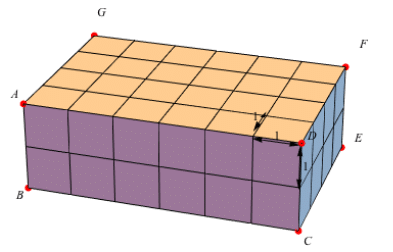
If we consider the front of this rectangular prism to be the base, we can see that it is made up of 12 cubes. There are four rows with 12 cubes in each row.
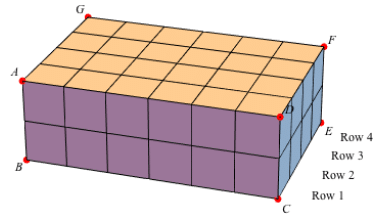
So, if we multiply the number of cubes in the base (12) by the number of rows (4), we find that there are 48 cubes. The prism has a volume of 48 cubic units.
We can also find the volume by measuring. The base of each cube is 1 unit wide and 1 unit high so its area is 1 unit2. Since there are 12 cubes in the base of the prism, the area of the prism base is 12 units2. The length of one cube is 1 unit, so the total length of the prism is 4 units. Notice that if we multiply the total area of the base (12 units2) by the total height of the base (4 units) we also get the area: 48 cubic units, or 48 units3.
Volume of a rectangular prism = (area of base) (height)
Let's look at another type of prism: a cube. The length, width, and height of a cube are all equal. It's a close relative to the square. A piece of origami paper (think thin, colorful, easy to fold) is a square, and a stack of origami paper is a cube if it's as high as the paper is wide (or long).

If each piece of origami paper is 5 inches long and 5 inches wide, the area of the piece of paper on the base of the stack is 25 inches2. In other words, the area of the base is 25 in2. If the stack is 5 inches high, then it has a volume of 25 in2 × 5 inches of paper, or 125 in3.
If we slide the top of the stack over, but the base stays where it is, we can make a leaning tower of Pisa, or an oblique prism. While the shape of the prism has changed a bit, the volume of the prism has not. The same amount of paper is still there. The volume of an oblique prism is also (area of base)(height), but the height has to be perpendicular to the base. In the case of the mysterious leaning tower of origami, the height is the distance from the top piece of paper straight down to the surface it sits on.
Volume of a square prism, or cube = (area of base)(height)
Not all prisms have a rectangular or square base. Think about those cool rainbow prisms you've seen in science.
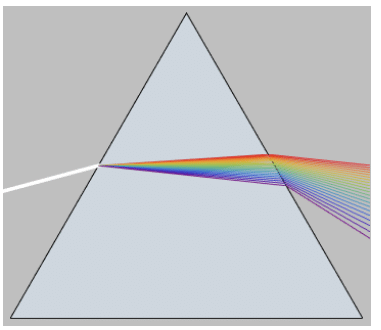
This is a triangular prism. The bases are triangles and the sides (or faces) are rectangles. It's just like the stack of origami paper, only the paper is now triangle shaped. And the volume formula is the same as well, the area of the triangle base (either one) is multiplied by the triangular prism's height.
Volume of a triangular prism = (area of base)(height)
Now let's look at a cylinder.
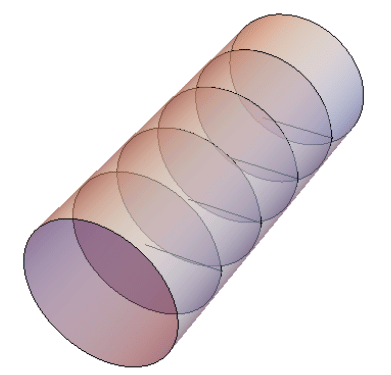
If the area of the circular base is equal to 16π square units, and each row is 1 unit high, with five rows of these circular bases, then the volume would be 16π units2 × 5 units = 80π cubic units, or approximately 251.2units3.
Volume of a cylinder = (area of base)(height)
Look Out: volume is always measured in cubic units (units3). This is because we are dealing with three-dimensional objects now. You're in the big time!
See the pattern in these formulas? They all multiply the area of the base by how tall the 3-D shape is. This is pretty much all you have to do to find the volume of any prism or cylinder: find the area of the base and multiply it by the height.
Volume of a Prism or Cylinder = area of the Base x height Volume = Bh
Look Out: note the difference between small "b" and large "B". In the examples above (and often in geometry in general), small "b" is the length of the base of a 2-D shape. Large "B" is the area of the base of a 3-D solid.
Volume Of Pyramids & Cones
The formula for the volume of pyramids and cones tells you how much space is inside each object.
For these two solid shapes, the volume formula is the same: it's one-third of the area of the base times the height.
Volume of Pyramids or Cones = ⅓ Area of Base × height = 1/3Bh
Area of base × height, or Bh? That looks familiar, but what's up with the 1/3? Picture this: a cone paper cup fits perfectly inside a cylinder cup. They're the same height and the round circles on top are also the same, which means the base of the cone and the base of the cylinder have the same area. How many paper cups of water does it take to fill the cylinder? Believe us when we say it takes 3, and a whole roll of paper towels to clean up the mess. The volume of three cones is equal to the volume of one cylinder with the same base and height. Similarly, the volume of three pyramids is real to the volume of one prism with the same base and height.
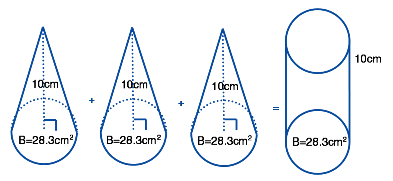
The volume of each cone is equal to ⅓Bh = ⅓(28.3 × 10) = 94 ⅓ cm3. The volume of all three cones combined equals 283 cm3. The volume of the cylinder is equal to Bh = 28.3 × 10 = 283 cm3. Ta-da!
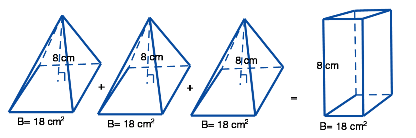
The volume of each pyramid is equal to ⅓Bh = ⅓(18 × 8) = 48 cm3. The volume of all three pyramids combined equals 144 cm3. The volume of the rectangular prism is equal to Bh = 18 × 8 = 144 cm3.
Volume Of Spheres
A ball is a sphere. A sphere is a 3-D shape. 3-D shapes have volume. So a ball has volume. What it doesn't have is a base. So our tried and true formula for volume: Base × height, or Bh, doesn't work sp-here (get it?). Luckily, a brilliant ancient Greek mathematician named Archimedes figured out a formula for the volume of a sphere that doesn't require the area of a base. It is: 4/3 × pi × the radius cubed, or 4/3 πr3.
Which came first, the circle or the sphere? They're eerily alike. A sphere has a center just like a circle does; it's the point in the middle of the sphere that is the same distance from every point on the sphere. A sphere has a diameter, just like a circle, and it goes from one point on the sphere, through the center, to another point on the sphere. And finally, just like a circle, the radius of a sphere is half the diameter. It's also the distance from the center to any point on the sphere.
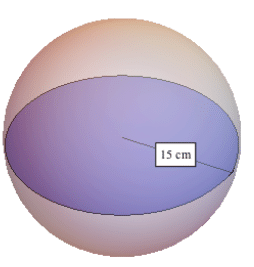
If the radius of a sphere is 15 cm, then the volume is 4/3 (π) (15)3 which is 4/3 π (3375 cm3) = 4500 π cm3 = 14,130 cm3.



































