What is Proportion? | The Complete SAT Course - Class 10 PDF Download
Proportion
Proportion is explained majorly based on ratio and fractions. A fraction, represented in the form of a/b, while ratio a : b, then a proportion states that two ratios are equal. Here, a and b are any two integers. The ratio and proportion are key foundations to understand the various concepts in mathematics as well as in science.
Proportion finds application in solving many daily life problems such as in business while dealing with transactions or while cooking, etc. It establishes a relation between two or more quantities and thus helps in their comparison.
What is Proportion?
Proportion, in general, is referred to as a part, share, or number considered in comparative relation to a whole. Proportion definition says that when two ratios are equivalent, they are in proportion. It is an equation or statement used to depict that two ratios or fractions are equal.
Proportion- Definition
Proportion is a mathematical comparison between two numbers. According to proportion, if two sets of given numbers are increasing or decreasing in the same ratio, then the ratios are said to be directly proportional to each other. Proportions are denoted using the symbol "::" or "=".
Proportion- Example
Two ratios are said to be in proportion when the two ratios are equal. For example, the time taken by train to cover 50km per hour is equal to the time taken by it to cover the distance of 250km for 5 hours. Such as 50km/hr = 250km/5hrs.
Continued Proportions
Any three quantities are said to be in continued proportion if the ratio between the first and the second is equal to the ratio between the second and the third. Similarly, four quantities in continued proportion will have the ratio between the first and second equal to the ratio between the third and fourth.
For example, consider two ratios to be a:b and c:d. In order to find the continued proportion for the two given ratio terms, we will convert their means to a single term/number. This in general, would be the LCM of means, and for the given ratio, the LCM of b & c will be bc. Thus, multiplying the first ratio by c and the second ratio by b, we have
- First ratio- ca : bc
- Second ratio- bc : bd
Thus, the continued proportion for the given ratios can be written in the form of ca : bc : bd.
Ratios and Proportions
The ratio is a way of comparing two quantities of the same kind by using division. The ratio formula for two numbers a and b is given by a : b or a/b. Multiply and dividing each term of a ratio by the same number (non-zero), doesn’t affect the ratio.
When two or more such ratios are equal, they are said to be in proportion.
Fourth, Third and Mean Proportional
If a : b = c : d, then:
- d is called the fourth proportional to a, b, c.
- c is called the third proportional to a and b.
- The mean proportional between a and b is √(ab).
Tips and Tricks on Proportion
- a/b = c/d ⇒ ad = bc
- a/b = c/d ⇒ b/a = d/c
- a/b = c/d ⇒ a/c = b/d
- a/b = c/d ⇒ (a + b)/b = (c + d)/d
- a/b = c/d ⇒ (a - b/b = (c - d)/d
- a/(b + c) = b/(c + a) = c/(a + b) and a + b + c ≠0, then a = b = c.
- a/b = c/d ⇒ (a + b)/(a - b) = (c + d)/(c - d), which is known as componendo -dividendo rule
- If both the numbers a and b are multiplied or divided by the same number in the ratio a:b, then the resulting ratio remains the same as the original ratio.
Proportion Formula with Examples
A proportion formula is an equation that can be solved to get the comparison values. To solve proportion problems, we use the concept that proportion is two ratios that are equal to each other. We mean this in the sense of two fractions being equal to each other.
Ratio Formula
Assume that, we have any two quantities (or two entities) and we have to find the ratio of these two, then the formula for ratio is defined as a:b ⇒ a/b, where,
- a and b could be any two quantities.
- “a” is called the first term or antecedent.
- “b” is called the second term or consequent.
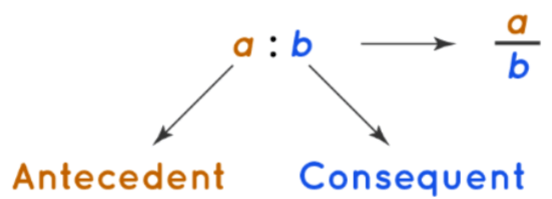
For example, in ratio 5 : 9, is represented by 5/9, where 5 is antecedent and 9 is consequent. 5 : 9 = 10 : 18 = 15 : 27
Proportion Formula
Now, let us assume that, in proportion, the two ratios are a:b and c:d. The two terms ‘b’ and ‘c’ are called ‘means or mean terms’, whereas the terms ‘a’ and ‘d’ are known as ‘extremes or extreme terms.’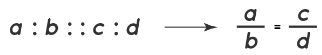
a/b = c/d or a : b : : c : d. For example, let us consider another example of the number of students in 2 classrooms where the ratio of the number of girls to boys is equal. Our first ratio of the number of girls to boys is 2 : 5 and that of the other is 4 : 8, then the proportion can be written as: 2 : 5 :: 4 : 8 or 2/5 = 4/8. Here, 2 and 8 are the extremes, while 5 and 4 are the means.
Types of Proportions
Based on the type of relationship two or more quantities share, the proportion can be classified into different types. There are two types of proportions.
- Direct Proportion
- Inverse Proportion
Direct Proportion and Inverse Proportion
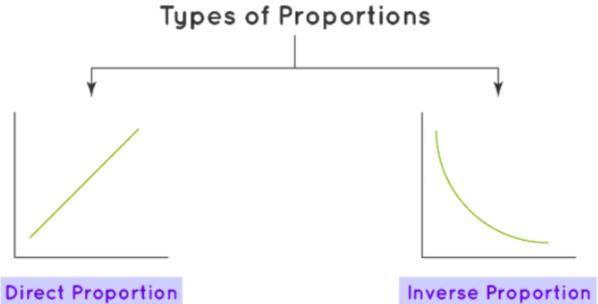
Direct Proportion
This type describes the direct relationship between two quantities. In simple words, if one quantity increases, the other quantity also increases and vice-versa. For example, if the speed of a car is increased, it covers more distance in a fixed amount of time. In notation, the direct proportion is written as y ∝ x.
Inverse Proportion
This type describes the indirect relationship between two quantities. In simple words, if one quantity increases, the other quantity decreases and vice-versa. In notation, an inverse proportion is written as y ∝ 1/x. For example, increasing the speed of the car will result in covering a fixed distance in less time.
Important Notes
- Proportion is a mathematical comparison between two numbers.
- Basic proportions are of two types: direct proportions and inverse proportions.
- We can apply the concepts of proportions to geography, comparing quantities in physics, dietetics, cooking, etc.
Properties of Proportion
Proportion establishes equivalent relation between two ratios. The properties of proportion that is followed by this relation:
- Addendo – If a : b = c : d, then value of each ratio is a + c : b + d
- Subtrahendo – If a : b = c : d, then value of each ratio is a – c : b – d
- Dividendo – If a : b = c : d, then a – b : b = c – d : d
- Componendo – If a : b = c : d, then a + b : b = c + d : d
- Alternendo – If a : b = c : d, then a : c = b: d
- Invertendo – If a : b = c : d, then b : a = d : c
- Componendo and dividendo – If a : b = c : d, then a + b : a – b = c + d : c – d
Difference Between Ratio and Proportion
Ratio and proportion are closely related concepts. Proportion signifies the equal relationship between two or more ratios. To understand the concept of ratio and proportion, go through the difference between ratio and proportion given here.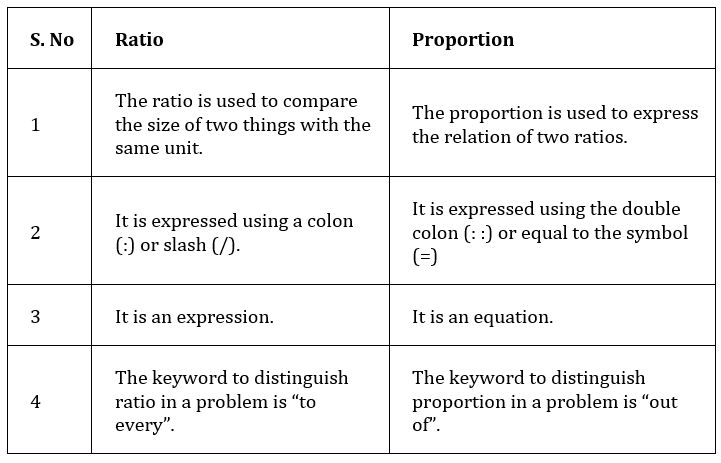
Example: Jessy runs 4 miles in 30 minutes. At this rate, how far could she run in 45 minutes?
Solution: Let's assume the unknown quantity here is x.
In this case, x is the number of miles Jessy can run in 45 minutes at the given rate.
It is given that running 4 miles in 30 minutes is the same as running x miles in 45 minutes.
The equation of proportion for the above case can be written as 4/30 = x/45, 30 × x = 4 × 45, x = 180/30 = 6.
Therefore, Jessy can run 6 miles in 45 minutes.
|
433 videos|220 docs|166 tests
|





















