What is Pythagoras theorem - Class 7 PDF Download
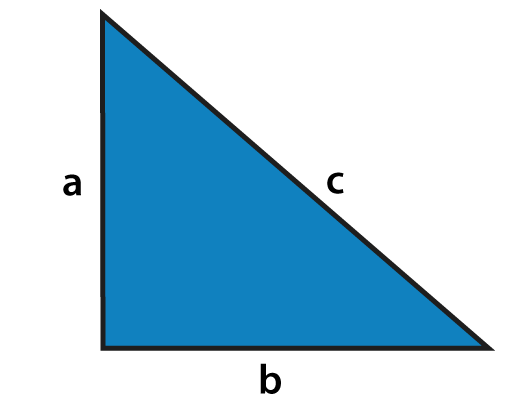
In a right-angled triangle, “The sum of squares of the lengths of the two sides is equal to the square of the length of the hypotenuse (or the longest side).”
a2+b2=c2
In the given triangle, side “a” is called as “Perpendicular”, side “b” is called as “Base” and side “c” is called as “Hypotenuse.”
The side opposite to the right angle (90∘) is the longest side known as Hypotenuse, as we know that the side opposite to the greatest angle is longest.
Note- Pythagoras theorem is only applicable to a Right-Angled triangle.
Another way of representation of the Pythagoras Theorem-
Another way of Pythagoras Theorem proof is described here. Consider a right-angled triangle having perpendicular as a, base as b, and hypotenuse as c. Consider three squares of sides a,b,c mounted on the three sides of a triangle having the same sides as shown.
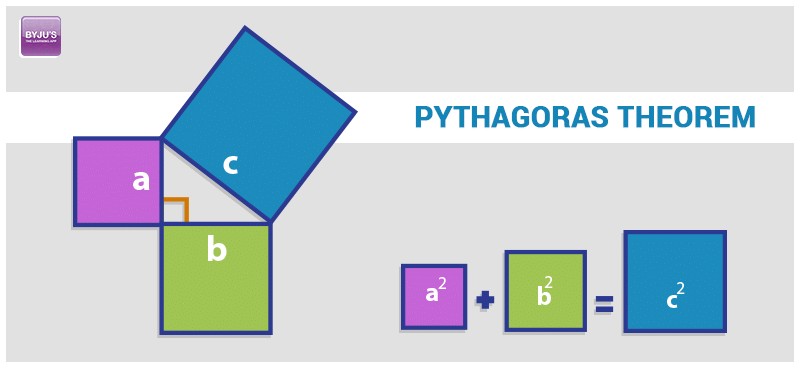 By Pythagoras Theorem –
By Pythagoras Theorem –
Area of square A + Area of square B = Area of square C
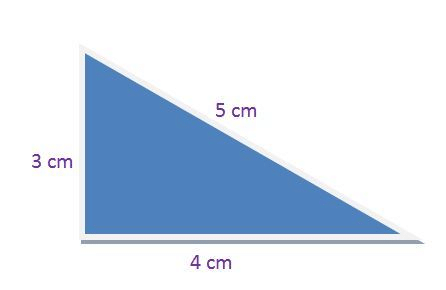
Example- Prove the Pythagoras Theorem for a right angle triangle having sides to be 3cm, 4cm and 5 cm.Solution –
From Pythagoras Theorem we have,
(Perpendicular)2+(base)2=(Hypotenuse)2
Perpendicular = 3 cm
Base = 4 cm
Hypotenuse = 5 cm
(3)2+(4)2=(5)2
⇒9+16=25
⇒25=25
L.H.S. = R.H.S.
Therefore Pythagoras theorem is proved.
Proof of Pythagoras Theorem-To Prove- AC2=AB2+BC2</p >
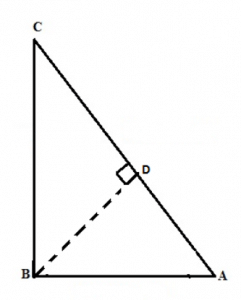 For this we drop a perpendicular BD onto the side ACWe know, △ADB∼△ABCTherefore, ADAB=ABAC (Condition for similarity)Or, AB2=AD×AC……..(1)Also, △BDC∼△ABCTherefore, CDBC=BCAC (Condition for similarity)Or, BC2=CD×AC……..(2)Adding the equations (1) and (2) we get,AB2+BC2=AD×AC+CD×ACAB2+BC2=AC(AD+CD)Since, AD + CD = ACTherefore, AC2=AB2+BC2Application-(1st): To know the triangle is right-angled or not. It is to be noted that if the Pythagoras Theorem is proved then it must be a right-angled triangle.
For this we drop a perpendicular BD onto the side ACWe know, △ADB∼△ABCTherefore, ADAB=ABAC (Condition for similarity)Or, AB2=AD×AC……..(1)Also, △BDC∼△ABCTherefore, CDBC=BCAC (Condition for similarity)Or, BC2=CD×AC……..(2)Adding the equations (1) and (2) we get,AB2+BC2=AD×AC+CD×ACAB2+BC2=AC(AD+CD)Since, AD + CD = ACTherefore, AC2=AB2+BC2Application-(1st): To know the triangle is right-angled or not. It is to be noted that if the Pythagoras Theorem is proved then it must be a right-angled triangle.Example- The sides of a triangle are 5,12 & 13 units. Check if it has a right angle or not.Solution-
To prove- Pythagoras theorem in order to find whether it has a right angle or not
From Pythagoras Theorem, we have-
(Perpendicular)2+(base)2=(Hypotenuse)2
Perpendicular = 12 units
Base = 5 units
Hypotenuse = 13 units
(12)2+(5)2=(13)2
⇒144+25=169
⇒169=169
L.H.S. = R.H.S.
Therefore the angles opposite to the 13 unit side will be at a right angle.

Example- The two sides of a right angled as shown in the figure. Find the third side.
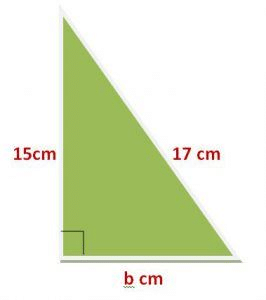
Solution-
Given-
Perpendicular = 15cm
Base = b cm
Hypotenuse = 17 cm
From Pythagoras Theorem, we have
(Perpendicular)2+(base)2=(Hypotenuse)2
152+b2=172
⇒225+b2=289
⇒b2=289–225
⇒b2=64
⇒b=64−−√
Therefore b=8
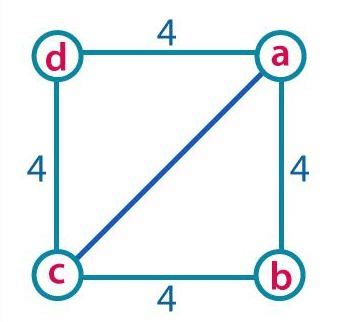
(3rd): To find the diagonal of a squareExample- Given the side of a square to be 4 cm. Find the length of the diagonal.Solution-
Given –
Sides of a square = 4 cm
To Find- The length of diagonal ac.
Consider triangle abc (or can also be acd)
(ab)2+(bc)2=(ac)2
⇒(4)2+(4)2=(ac)2
⇒16+16=(ac)2
⇒32=(ac)2
⇒(ac)2=32
or acl=42–√