Best Study Material for Class 5 Exam
Class 5 Exam > Class 5 Notes > Mathematics for Class 5: NCERT > Word Problems: How Big, How Heavy
Word Problems: How Big, How Heavy | Mathematics for Class 5: NCERT PDF Download
Q1. Find the volume of a cuboid of length 4 cm, breadth 2 cm and height 3 cm?
Ans: The volume of a cuboid can be calculated using the formula:
- Volume = length (l) × breadth (b) × height (h)
Given the dimensions:
- Length = 4 cm
- Breadth = 2 cm
- Height = 3 cm
Substituting the values into the formula:
- Volume = 4 cm × 2 cm × 3 cm = 24 cubic centimetres (cu cm)
Thus, the volume of the cuboid is 24 cu cm.
Q2. A water tank has length 9 cm, breadth 7 cm and height 5 cm. How many cubic metre of water can it hold?
Ans: Given the dimensions of the water tank:
- Length (l) = 9 cm
- Breadth (b) = 7 cm
- Height (h) = 5 cm
The volume of the tank can be calculated using the formula: Volume = l × b × h = 9 cm × 7 cm × 5 cm = 315 cubic centimetres (cu cm).
To convert this volume into cubic metres, we use the conversion factor where 1 cubic metre equals 1,000,000 cubic centimetres: Therefore, the volume in cubic metres is: Volume in cubic metres = 315 cu cm / 1,000,000 = 0.000315 cubic metres.
Q3. Find the volume of a cuboid of side 8cm x 6 cm x 5 cm and a cube of side 9 cm.
Ans: The volume of a cuboid can be calculated using the formula: Volume of a cuboid = length (l) × breadth (b) × height (h) For the given cuboid:
- l = 8 cm
- b = 6 cm
- h = 5 cm
Thus, the volume is: Volume of a cuboid = 8 cm × 6 cm × 5 cm = 240 cm³
For the cube, the volume can be calculated using the formula: Volume of a cube = side × side × side For the cube:
- side = 9 cm
Therefore, the volume is: Volume of a cube = 9 cm × 9 cm × 9 cm = 729 cm³ In conclusion, the cuboid has a volume of 240 cm³, while the cube has a greater volume of 729 cm³.
Q4. A 2 rupee coin weighs 6g. What is the weight of a sack with:
(a) 1500 coins?
(b) 3000 coins?
Ans: Weight of a two-rupee coin = 6 g
- (a) Weight of a sack with 1500 coins = 1500 x 6 = 9000 g = 9 kg
- (b) Weight of a sack with 3000 coins = 3000 x 6 = 18000 g = 18 kg
Q5. The length, breadth and height of the inside of a rectangular box are 100 cm, 80 cm and 60 cm. How many centimeter cubes can be fitted in that box?
Ans: Given the dimensions of the rectangular box:
- Length (l) = 100 cm
- Breadth (b) = 80 cm
- Height (h) = 60 cm
The volume of the box can be calculated using the formula: Volume = l × b × h = 100 cm × 80 cm × 60 cm = 480,000 cubic centimetres (cu cm). Therefore, this box can hold 480,000 cubic centimetres, which means 480,000 unit cubes of 1 cm³ can fit inside it.
Q6. A brick is 24 cm long, 14 cm wide and 10 cm high. Find the space occupied by 500 such bricks?
Ans: Given the dimensions of the brick:
- Length (l) = 24 cm
- Width (b) = 14 cm
- Height (h) = 10 cm
The volume of one brick can be calculated using the formula: Volume = l × b × h = 24 cm × 14 cm × 10 cm = 3360 cm³. To find the space occupied by 500 such bricks, we multiply the volume of one brick by the number of bricks: Total Volume = 500 × 3360 cm³ = 1680000 cm³. Thus, the space occupied by 500 bricks is 1680000 cm³.
Q7. The volume of 6 marbles is 5 ml. Then find the volume of
(a) 24 such marbles
(b) 30 such marbles.
Ans:
Since 6 marbles have a total volume of 5 ml, we can find the volume of one marble by dividing:
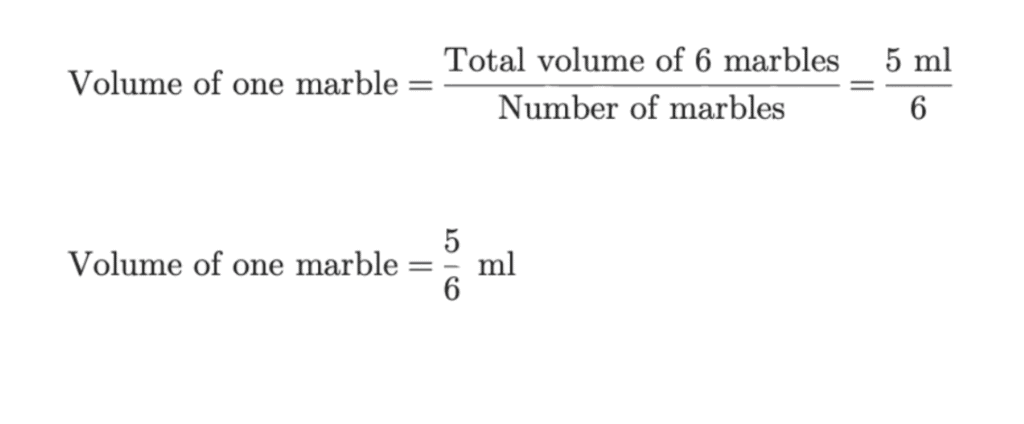
Since one marble has a volume of 5/6 ml, the volume of 24 marbles is:
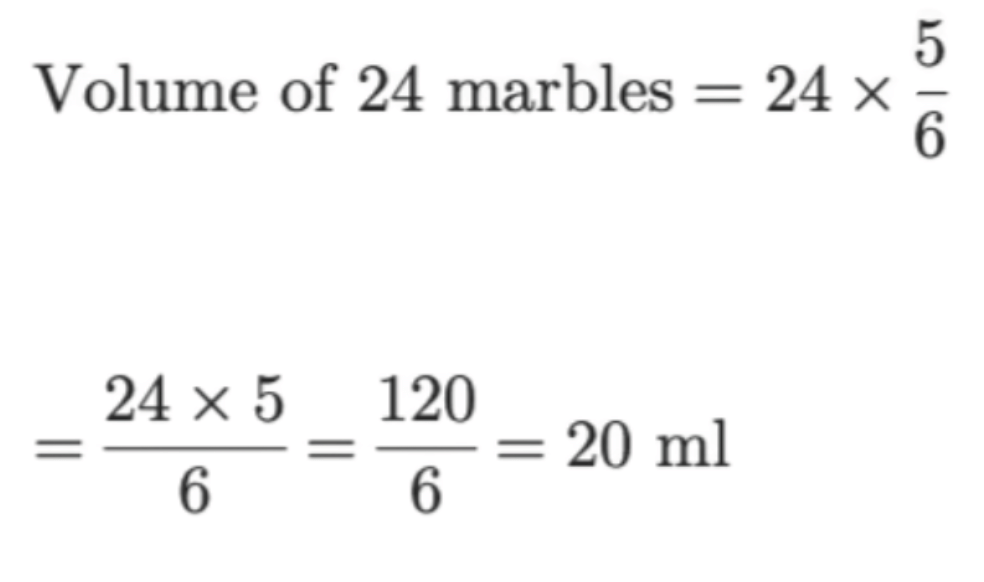
Similarly, for 30 marbles:
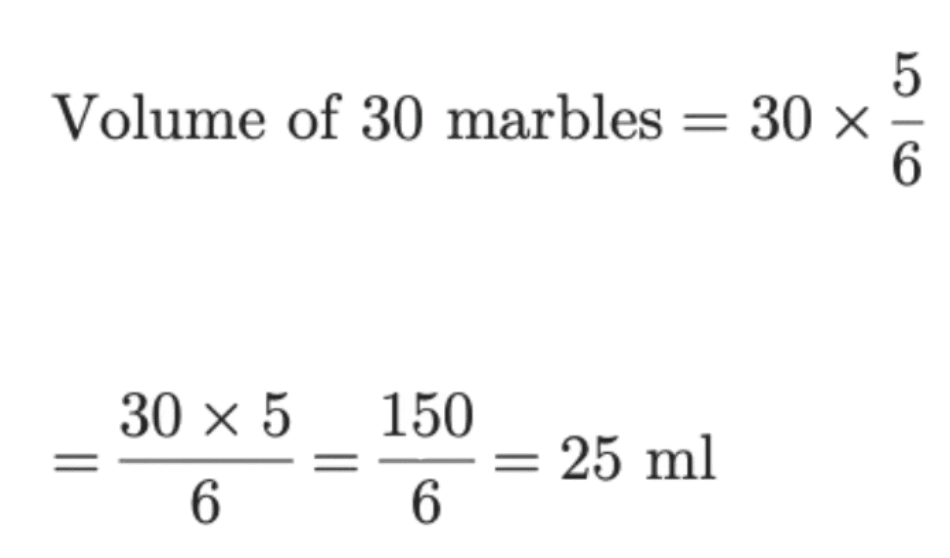
Q8. A match box measure 6 cm x 5 cm x 4 cm. Find its volume?
Ans: The volume of a matchbox can be calculated using the formula:
- Volume = length (l) × breadth (b) × height (h)
For the given matchbox dimensions:
- Length (l) = 6 cm
- Breadth (b) = 5 cm
- Height (h) = 4 cm
Substituting the values into the formula:
- Volume = 6 cm × 5 cm × 4 cm = 120 cm³
Thus, the volume of the matchbox is 120 cubic centimetres.
Q9. Find the volume of a cube whose edge is 15cm long?
Ans: The volume of a cube can be calculated using the formula:
- Volume = length × breadth × height
For a cube, all edges are equal, so we can simplify this to:
- Volume = edge × edge × edge
Given that the length of each edge is 15 cm, the calculation becomes:
- Volume = 15 cm × 15 cm × 15 cm = 3375 cm³
Therefore, the volume of the cube is 3375 cubic centimetres.
Q10. How many cubes of side 5 cm can be packed in a box of 30 cm x 25 cm x 20 cm?
Ans: To determine how many cubes with a side length of 5 cm can fit into a box with dimensions 30 cm x 25 cm x 20 cm, we first calculate the volume of the box.
- The volume of a cuboid is calculated using the formula: Volume = length x breadth x height
- Substituting the given values: Volume = 30 cm x 25 cm x 20 cm = 15000 cu cm
- Next, we calculate the volume of one cube: Volume of one cube = side x side x side = 5 cm x 5 cm x 5 cm = 125 cu cm
- To find out how many cubes can fit inside the box, we divide the volume of the box by the volume of one cube: Number of cubes = Volume of the box / Volume of one cube = 15000 cu cm / 125 cu cm = 120
- Therefore, a total of 120 cubes can be packed in the box.
The document Word Problems: How Big, How Heavy | Mathematics for Class 5: NCERT is a part of the Class 5 Course Mathematics for Class 5: NCERT.
All you need of Class 5 at this link: Class 5
|
31 videos|192 docs|41 tests
|
FAQs on Word Problems: How Big, How Heavy - Mathematics for Class 5: NCERT
| 1. What are some examples of word problems related to size and weight for Class 5 students? |  |
| 2. How can I help my child understand word problems better? | |
Ans. To help your child, encourage them to read the problem carefully, identify the key information, and visualize the scenario. Practicing with various examples and breaking down the problems into smaller, manageable parts can also be beneficial.
| 3. What strategies can be used to solve word problems about size and weight? | |
Ans. Some effective strategies include drawing diagrams, using physical objects for hands-on learning, creating equations based on the information given, and checking the work by substituting answers back into the original problem.
| 4. How do I teach my child to convert units of measurement in word problems? | |
Ans. Teach your child the basic conversion factors (e.g., 1000 grams = 1 kilogram, 100 cm = 1 meter) and practice converting units together. Provide examples where they need to convert units to solve a problem, reinforcing the concept through repetition.
| 5. Are there any online resources or worksheets for practicing word problems on size and weight? | |
Ans. Yes, there are many online resources such as educational websites that offer free worksheets and interactive games on word problems. Websites like Khan Academy, Education.com, and Math-Aids.com provide a variety of practice materials specifically for Class 5 students.
Related Exams
About this Document
4.62/5
Rating
Apr 12, 2025
Last updated
Document Description: Word Problems: How Big, How Heavy for Class 5 2025 is part of Mathematics for Class 5: NCERT preparation.
The notes and questions for Word Problems: How Big, How Heavy have been prepared according to the Class 5 exam syllabus. Information about Word Problems: How Big, How Heavy covers topics
like and Word Problems: How Big, How Heavy Example, for Class 5 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Word Problems: How Big, How Heavy.
Introduction of Word Problems: How Big, How Heavy in English is available as part of our Mathematics for Class 5: NCERT
for Class 5 & Word Problems: How Big, How Heavy in Hindi for Mathematics for Class 5: NCERT course.
Download more important topics related with notes, lectures and mock test series for Class 5
Exam by signing up for free. Class 5: Word Problems: How Big, How Heavy | Mathematics for Class 5: NCERT
Description
Full syllabus notes, lecture & questions for Word Problems: How Big, How Heavy | Mathematics for Class 5: NCERT - Class 5 | Plus excerises question with solution to help you revise complete syllabus for Mathematics for Class 5: NCERT | Best notes, free PDF download
Information about Word Problems: How Big, How Heavy
In this doc you can find the meaning of Word Problems: How Big, How Heavy defined & explained in the simplest way possible. Besides explaining types of
Word Problems: How Big, How Heavy theory, EduRev gives you an ample number of questions to practice Word Problems: How Big, How Heavy tests, examples and also practice Class 5
tests
Related Searches
Previous Year Questions with Solutions
,Exam
,study material
,Sample Paper
,MCQs
,practice quizzes
,Summary
,How Heavy | Mathematics for Class 5: NCERT
,Viva Questions
,Word Problems: How Big
,Word Problems: How Big
,Objective type Questions
,Free
,shortcuts and tricks
,ppt
,Semester Notes
,mock tests for examination
,past year papers
,How Heavy | Mathematics for Class 5: NCERT
,video lectures
,Important questions
,How Heavy | Mathematics for Class 5: NCERT
,Extra Questions
,Word Problems: How Big
;
Additional Information about Word Problems: How Big, How Heavy for Class 5 Preparation
Word Problems: How Big, How Heavy Free PDF Download
The Word Problems: How Big, How Heavy is an invaluable resource that delves deep into the core of the Class 5 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Word Problems: How Big, How Heavy now and kickstart your journey towards success in the Class 5 exam.
Importance of Word Problems: How Big, How Heavy
The importance of Word Problems: How Big, How Heavy cannot be overstated, especially for Class 5 aspirants.
This document holds the key to success in the Class 5 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Word Problems: How Big, How Heavy Notes
Word Problems: How Big, How Heavy Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Word Problems: How Big, How Heavy.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Word Problems: How Big, How Heavy Notes on EduRev are your ultimate resource for success.
Word Problems: How Big, How Heavy Class 5 Questions
The "Word Problems: How Big, How Heavy Class 5 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 5 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Word Problems: How Big, How Heavy on the App
Students of Class 5 can study Word Problems: How Big, How Heavy alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Word Problems: How Big, How Heavy,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Word Problems: How Big, How Heavy is prepared as per the latest Class 5 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup