Word Problems: Patterns in Mathematics | Maths Olympiad Class 6 PDF Download
Q1: Aisha is counting the number of beads she places in a pattern each day. Day 1: 1 bead, Day 2: 3 beads, Day 3: 5 beads... and so on. How many beads does she place on Day 10?
Sol:
This is a pattern of odd numbers: 1, 3, 5, 7, 9...
The formula to find the nth odd number is: 2n - 1
Here, n = 10 → 2 × 10 − 1 = 20 − 1 = 19 beads
Answer: Aisha places 19 beads on Day 10.
Q2: Rohan collects stamps in this pattern: Day 1: 2 stamps, Day 2: 4 stamps, Day 3: 6 stamps... and so on. How many stamps does he collect on Day 8?
Sol:
This is a pattern of even numbers: 2, 4, 6, 8...
Formula: 2n
Here, n = 8 → 2 × 8 = 16 stamps
Answer: Rohan collects 16 stamps on Day 8.
Q3: Maya arranges chairs in triangle shapes: Pattern 1: 1 chair, Pattern 2: 3 chairs, Pattern 3: 6 chairs... and so on. How many chairs are in the 7th pattern?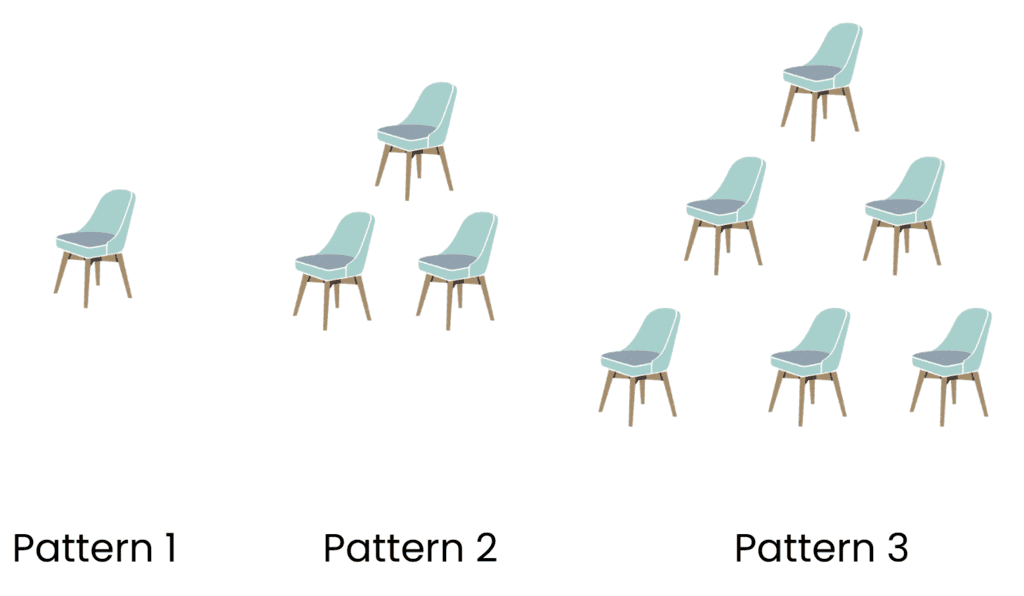
Sol:
This is a triangular number pattern.
Formula: n(n + 1) ÷ 2
Here, n = 7 → 7 × 8 ÷ 2 = 56 ÷ 2 = 28 chairs
Answer: There are 28 chairs in the 7th pattern.
Q4: A square-shaped courtyard is tiled in layers: Layer 1: 1 tile, Layer 2: 4 tiles, Layer 3: 9 tiles ... and so on. How many tiles are there in Layer 6?
Sol:
This is a pattern of square numbers: 1², 2², 3²...
Here, n = 6 → 6² = 36 tiles
Answer: There are 36 tiles in Layer 6.
Q5: A candle burns down by 2 cm every hour. Start height: 30 cm. What is the height after 5 hours?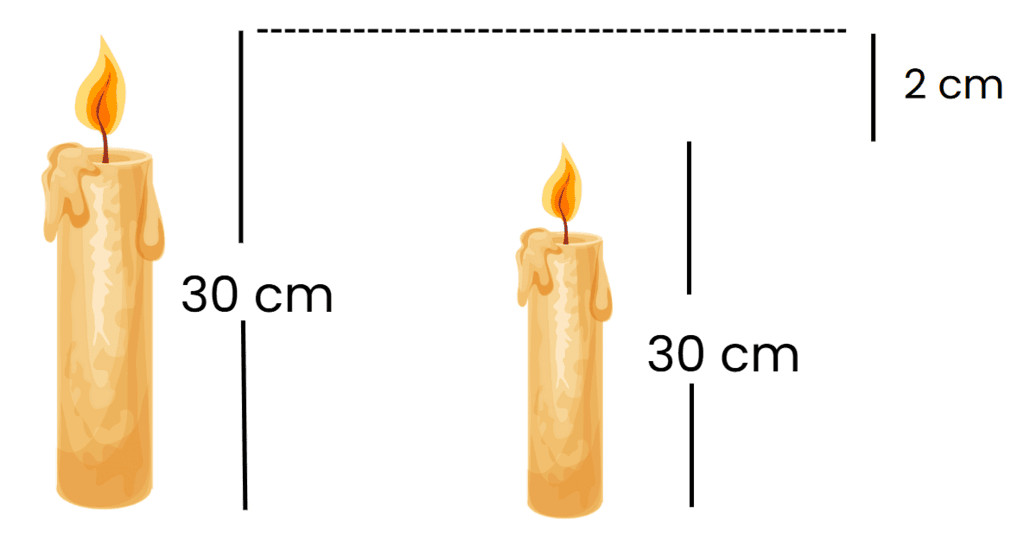
Sol:
Each hour, it decreases by 2 cm.
So, total decrease = 5 × 2 = 10 cm
New height = 30 - 10 = 20 cm
Answer: The height of the candle after 5 hours is 20 cm.
Q6: A pattern is made with square floor tiles: Row 1: 1 tile, Row 2: 2 tiles, Row 3: 3 tiles ... and so on. How many tiles are needed for Row 15?
Sol:
It is a simple counting pattern. Row n has n tiles.
So, Row 15 has 15 tiles.
Answer: 15 tiles are needed for Row 15.
Q7: Sneha saves ₹5 on Day 1, ₹10 on Day 2, ₹15 on Day 3... How much has she saved in total by Day 5?
Sol:
This is an arithmetic sequence: 5, 10, 15, 20, 25
Total = 5 + 10 + 15 + 20 + 25 = ₹75
Answer: Sneha has saved ₹75 in total by Day 5.
Q8: A plant grows 3 cm daily. Start: 5 cm. How tall after 10 days?
Sol:
Growth in 10 days = 10 × 3 = 30 cm
Total height = 5 + 30 = 35 cm
Answer: The plant will be 35 cm tall after 10 days.
Q9: A block pyramid is built layer by layer: Layer 1: 1 block, Layer 2: 3 blocks, Layer 3: 5 blocks... How many blocks in Layer 9?
Sol:
This follows odd numbers. Formula = 2n − 1
Here, n = 9
⇒ 2 × 9 − 1 = 18 − 1 = 17 blocks
Answer: Layer 9 has 17 blocks.
Q10: Ravi reads 5 more pages than the previous day: Day 1: 10 pages. How many pages on Day 6?
Sol:
This is an arithmetic sequence with a = 10, d = 5
Using formula: a + (n − 1)d
Here, a = 10, d = 5, n = 6
⇒ 10 + (6 − 1) × 5 = 10 + 25 = 35
Answer: Ravi reads 35 pages on Day 6.
Q11: A farmer places posts at equal gaps: 1st post at 0 m, then every 3 m. How many posts till 30 m?
Sol:
Posts at: 0, 3, 6, ..., 30
These are multiples of 3
Number of posts = (30 ÷ 3) + 1 = 10 + 1 = 11
Answer: The farmer places 11 posts till 30 m.
Q12: A paper is folded, doubling each time: Fold 1: 2 layers, Fold 2: 4 layers, Fold 3: 8 layers... How many layers after Fold 6?
Sol:
This is a power of 2 pattern:
Here, Fold 6: 2⁶ = 64
Answer: There are 64 layers after Fold 6.
Q13: Tiling pattern: 1, 6, 11, 16... Find number of tiles in the 9th pattern.
Sol:
This is an arithmetic sequence. First term , common difference
Using formula:
= a + (n − 1)d
⇒ 1 + (9 − 1) × 5 = 1 + 40 = 41
Answer: The 9th pattern has 41 tiles.
Q14: Petal pattern follows Fibonacci: 1, 1, 2, 3, 5, 8, ... How many petals on the 8th flower?
Sol:
We are given a Fibonacci pattern:
1, 1, 2, 3, 5, 8, ...
In the Fibonacci pattern, each number is the sum of the two previous numbers.
Let’s write the petals on each flower:
1st flower = 1 petal
2nd flower = 1 petal
3rd flower = 1 + 1 = 2 petals
4th flower = 1 + 2 = 3 petals
5th flower = 2 + 3 = 5 petals
6th flower = 3 + 5 = 8 petals
7th flower = 5 + 8 = 13 petals
8th flower = 8 + 13 = 21 petals
Answer: The 8th flower has 21 petals.
Q15: Soham jumps 2 more steps each time: Jump 1: 2 steps, Jump 2: 4 steps, Jump 3: 6 steps... How many steps in Jump 10?
Sol:
This is a pattern of even numbers: 2, 4, 6, 8...
Formula: 2 × n
Here, n = 10
⇒ 2 × 10 = 20
Answer: Soham jumps 20 steps in Jump 10.
Q16: Each new shelf in a library holds 5 more books than the last. First shelf: 10 books. How many on Shelf 7?
Sol:
This is an arithmetic sequence where:
First term (a) = 10, Common difference (d) = 5, Number of terms (n) = 7
Formula: a + (n − 1) × d
⇒ 10 + (7 − 1) × 5 = 10 + 30 = 40
Answer: Shelf 7 holds 40 books.
Q17: A stage has steps in triangular shape: 1 step, 3 steps, 6 steps... How many steps in the 5th row?
Sol:
This is a triangular number pattern.
Formula: n(n + 1) ÷ 2
Here, n = 5
⇒ 5 × 6 ÷ 2 = 30 ÷ 2 = 15
Answer: The 5th row has 15 steps.
Q18: A machine adds 4 blocks every minute. How many blocks after 12 minutes if it starts with 0?
Sol:
Blocks added = 12 × 4 = 48
Answer: The machine adds 48 blocks in 12 minutes.
Q19: A spiral has tiles placed in square numbers: 1, 4, 9, 16... How many tiles in the 10th square?
Sol:
This is a square number pattern.
10² = 100
Answer: The 10th square has 100 tiles.
Q20: Zara builds towers adding 1 more block than before: Tower 1: 1 block, Tower 2: 2 blocks, Tower 3: 3 blocks... How many blocks in total after 6 towers?
Sol:
This is a simple sum of the first 6 natural numbers.
Total = 1 + 2 + 3 + 4 + 5 + 6 = 21
Answer: Zara uses 21 blocks to build 6 towers.
|
30 videos|120 docs|59 tests
|
FAQs on Word Problems: Patterns in Mathematics - Maths Olympiad Class 6
| 1. What are the key concepts of patterns in mathematics for Class 6? |  |
| 2. How can I help my child understand patterns better in math? |  |
| 3. What types of problems can be expected in a Class 6 math exam on patterns? |  |
| 4. Are there any fun activities to teach patterns in mathematics? |  |
| 5. How can patterns be applied in everyday life? |  |

















