Word Problems: Quadrilaterals | Mathematics Class 8- New NCERT (Ganita Prakash) PDF Download
Q1: A quadrilateral has three acute angles, each measure 80°. What is the measure of the fourth angle?
Solution:
Let x be the measure of the fourth angle of a quadrilateral.
Sum of the four angles of a quadrilateral = 360°
80° + 80° + 80° + x = 360°
x = 360° – (80° + 80° + 80°)
x = 360° – 240°
x = 120°
Hence, the fourth angle is 120°.
Q2: In a quadrilateral ABCD, the measure of the three angles A, B and C of the quadrilateral is 110°, 70° and 80°, respectively. Find the measure of the fourth angle.
Solution: Let,
∠A = 110°
∠B = 70°
∠C = 80°
∠D = x
We know that the sum of all internal angles of quadrilateral ABCD is 360°.
∠A + ∠B+ ∠C+∠D = 360°
110° + 70° + 80° + x = 360°
260° + x = 360°
x = 360° – 260°
x = 100°
Therefore, the fourth angle is 100°.
Q3: The opposite angles of a parallelogram are (3x + 5)° and (61 – x)°. Find the measure of four angles.
Solution:
Given,
(3x + 5)° and (61 – x)° are the opposite angles of a parallelogram.
We know that the opposite angles of a parallelogram are equal.
Therefore,
(3x + 5)° = (61 – x)°
3x + x = 61° – 5°
4x = 56°
x = 56°/4
x = 14°
⇒ 3x + 5 = 3(14) + 5 = 42 + 5 = 47
61 – x = 61 – 14 = 47
The measure of angles adjacent to the given angles = 180° – 47° = 133°
Hence, the measure of four angles of the parallelogram are 47°, 133°, 47°, and 133°.
Q4: A diagonal and a side of a rhombus are of equal length. Find the measure of the angles of the rhombus.
Solution:
Let ABCD be the rhombus.
Thus, AB = BC = CD = DA
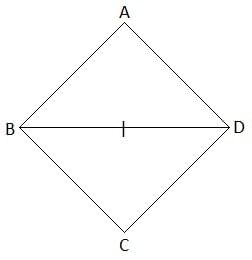 Given that a side and diagonal are equal.
Given that a side and diagonal are equal.
AB = BD (say)
Therefore, AB = BC = CD = DA = BD
Now, all the sides of a triangle ABD are equal.
Therefore, ΔABD is an equilateral triangle.
Similarly,
ΔBCD is also an equilateral triangle.
Thus, ∠A = ∠ABD = ∠ADB = ∠DBC = ∠C = ∠CDB = 60°
∠B = ∠ABD + ∠DBC = 60° + 60° = 120°
And
∠D = ∠ADB + ∠CDB = 60° + 60° = 120°
Hence, the angles of the rhombus are 60°, 120°, 60° and 120°.
Q5: In a trapezium PQRS, PQ || RS, ∠P : ∠S = 3 : 2 and ∠Q : ∠R = 4 : 5. Find the angles of the trapezium.
Solution:
Given,
∠P : ∠S = 3 : 2
∠Q : ∠R = 4 : 5
Let 3x and 2x be the measures of angles P and S.
And let 4x and 5x be the measures of angle Q and R.
As we know, the sum of adjacent angles at the corners of non-parallel sides of a trapezium = 360°
∠P + ∠S = 180°
3x + 2x = 360°
5x = 180°
x = 180°/5 = 36°
So, 3x = 3(36°) = 108°
2x = 2(36°) = 72°
Similarly,
4x + 5x = 180°
9x = 180°
x = 180°/9 = 20°
So, 4x = 4(20°) = 80°
5x = 5(20°) = 100°
Therefore, the angles of the trapezium are ∠P = 108°, ∠Q = 80, ∠R = 100 and ∠S = 72.
Q6: The diagonals of a rhombus are 12 cm and 7.5 cm. Find the area of a rhombus.
Solution:
Given: Length of diagonal 1 = 12 cm
Length of diagonal 2 = 7.5 cm
We know that,
Area of a rhombus = (1/2) × Diagonal 1× Diagonal 2 square units
A = (½)×12×7.5
A = 6×7.5
A = 45 cm2
Hence, the area of a rhombus is 45 cm2.
Q7: ABCD is a quadrilateral, whose angles are ∠A = 5(a+2)°, ∠B = 2(2a+7)°, ∠C = 64°, ∠D = ∠C-8°. Determine the value of ∠A.
Solution:
Given that, ∠A = 5(a+2)°, ∠B = 2(2a+7)°, ∠C = 64°, ∠D = ∠C-8°
Hence, ∠D = 64° – 8°
∠D = 56°
As we know,
∠A+∠B+∠C+∠D = 360°
Now, substitute the values, we get
5(a+2)° + 2(2a+7)° + 64°+56° = 360°
5a°+10°+4a°+14° +64° +56° = 360°
9a° + 144° = 360°
9a° = 360° – 144°
9a° = 216°
a° = 216°/9
a° = 24°
Hence, the value of ∠A is:
∠A = 5(a+2)° = 5(24°+2°) = 5 (26°) = 130°
Therefore, ∠A = 130°.
Q8: The three angles of a quadrilateral are 60°, 90°, 110°. Determine the fourth angle.
Solution:
We know that the sum of interior angles of a quadrilateral is 360°.
Given three angles are 60°, 90° and 110°.
Let the unknown angle be “x”.
By using the property of quadrilateral,
60° + 90° + 110° + x = 360°
260° + x = 360°
x = 360° – 260°
x = 100°.
Hence, the fourth angle of a quadrilateral is 100°.
Q9: If the diagonals of a rhombus are 12 cm and 7.5 cm, what is the area of the rhombus?
Solution:
Given: Length of diagonal 1 = 12 cm
Length of diagonal 2 = 7.5 cm
We know that,
Area of a rhombus = (1/2) × Diagonal 1× Diagonal 2 square units
A = (½)×12×7.5
A = 6×7.5
A = 45 cm 2
Hence, the area of a rhombus is 45 cm 2 .
Q10: If two angles of a quadrilateral are 76° and 68°, and the other two angles are in the ratio of 5: 7, what are the measures of these two angles?
Solution:
Given that two angles are 76° and 68°.
Let's denote the other two angles as 5x and 7x.
As we know, the sum of interior angles of a quadrilateral is 360°.
Therefore, 76°+68°+5x + 7x = 360°
144° + 12x = 360°
12x = 360° – 144°
12x = 216°
x = 216°/12
x = 18°
Hence, the other two angles are:
5x = 5(18)° = 90°
7x = 7(18°) = 126°.
|
26 videos|177 docs|11 tests
|
FAQs on Word Problems: Quadrilaterals - Mathematics Class 8- New NCERT (Ganita Prakash)
| 1. What are the properties of quadrilaterals? |  |
| 2. How do you calculate the area of different types of quadrilaterals? |  |
| 3. What is the difference between a convex and concave quadrilateral? |  |
| 4. Can you provide examples of real-life applications of quadrilaterals? |  |
| 5. How do you identify different types of quadrilaterals based on their sides and angles? |  |





















