Enthalpy, Heat, Internal Energy & Work Done Calculations in Different Processes

Table of Contents
1. Enthalpy, Heat, Internal Energy & Work Done Calculations in Different Processes
2. (1) Isochoric process
3. (2) Isobaric process
4. (3) Isothermal process
5. Worked Examples - Isothermal / Isobaric / Isochoric Processes
6. (4) Adiabatic Ideal Gas Expansion & Compression
7. Worked Examples - Adiabatic Processes
8. Comparison of Reversible Isothermal and Reversible Adiabatic Ideal Gas Expansion
View more

Enthalpy, Heat, Internal Energy & Work Done Calculations in Different Processes

(1) Isochoric process

Definition. Volume is constant during the process: V = constant.

dV = 0

dU = dq_V

ΔU = q_V = n C_V ΔT

Calculation of q, w, ΔH, ΔU for an IRREVERSIBLE ISOCHORIC process involving an ideal gas:

Since dV = 0, the work done w = 0.

(2) Isobaric process

Definition. Pressure is constant during the process: P = constant.

General expression for work

W = -P_ext (V₂ - V₁)

Reversible & isobaric process

For a reversible isobaric process where P_ext = P (system pressure),

W = -P (V₂ - V₁) = -nR (T₂ - T₁)

Irreversible & isobaric process

If P_ext = P₁ = P₂ = constant, the numerical value of work for reversible and irreversible isobaric (or isochoric) processes is the same because the pressure against which the system expands/compresses is the same.

(3) Isothermal process

(a) Reversible expansion or compression

Definition. Temperature remains constant: T = constant.

For an ideal gas in a reversible isothermal process the work done is

W = - ∫ P dV = - ∫ (nRT / V) dV = - nRT ln (V₂ / V₁)

Because ΔU = 0 for an ideal gas in an isothermal change,

Calculation of q, w, ΔH, ΔU for a reversible isothermal process involving an ideal gas:

ΔU = q + w = 0 ⇒ q = -w

(b) Single-stage irreversible expansion

Work done for a single-stage (free or against constant external pressure) irreversible expansion:

W = -P_ext (V₂ - V₁)

In the case of expansion, the magnitude of reversible work is greater than that of a single-step irreversible expansion:

|W_rev| > |W_irr|

(c) Two-stage irreversible expansion

Stage I. P_ext = 3 atm, P_i = 5 atm

Stage II. P_ext = 2 atm, P_f = 2 atm

Work done in second stage is greater than work done in first stage because the external pressure in the second stage acts over a larger volume change at lower resisting pressure.

(d) n-stage expansion and one-stage compression

Compression - one stage compression

|W_irr| = P_ext ΔV

Example values: P₁ = 1 atm, P₂ = 5 atm, P_ext = 5 atm

For compression, the magnitude of irreversible work is larger than reversible work:

|W_irr| > |W_rev|

Calculation of q, w, ΔH, ΔU for an irreversible isothermal process involving an ideal gas

For an isothermal process of an ideal gas ΔT = 0, therefore

ΔH = 0 and ΔU = 0

Work is determined solely by the external pressure path:

For an isobaric process (related expressions):

When P_ext = P (constant pressure) the work expression can be written as

= - nR (T₂ - T₁) = - nR ΔT

Worked Examples - Isothermal / Isobaric / Isochoric Processes

Example 1. 2 moles of an ideal gas initially present in a piston fitted cylinder at 300 K, and 10 atm are allowed to expand against 1 atm but the piston was stopped before it established the mechanical equilibrium. If temperature were maintained constant throughout the change and system delivers 748.26 J of work, determine the final gas pressure and describe the process on PV diagram.

Solution.

W_irr = -748.26 J

For an irreversible isothermal expansion against constant external pressure,

W_irr = - P_ext (V₂ - V₁) = - P_ext nRT (1/P₂ - 1/P₁)

Rearrange to find P₂.

Substitution and algebra give P₂ = 4 atm.

The PV diagram corresponds to an isothermal horizontal line (constant T) where the system expands from P=10 atm towards lower pressure but stops at P=4 atm because the piston was halted before reaching equilibrium with P_ext = 1 atm.

Example 2. 1150 Kcal heat is released when following reaction is carried out at constant volume.

C₇H_16(l) + 11 O_2(g) → 7 CO_2(g) + 8 H₂O(l)

Find the heat change at constant pressure.

Also: The pressure of liquid is a linear function of volume (P = a + bV) and the internal energy of the liquid is U = 34 + 3PV. Find a, b, w, ΔE & ΔH for change in state from 100 Pa, 3 m³ to 400 Pa, 6 m³.

Solution.

From P = a + bV:

100 = a + 3b

400 = a + 6b

Subtract the first from the second:

300 = 3b ⇒ b = 100

Substitute back: 100 = a + 3(100) ⇒ a = -200

Internal energy expression: U = 34 + 3 P V

ΔU = U₂ - U₁ = 3 (P₂ V₂ - P₁ V₁)

Compute P₂ V₂ - P₁ V₁ = (400×6) - (100×3) = 2400 - 300 = 2100

ΔU = 3 × 2100 = 6300 J

ΔH = ΔU + (P₂ V₂ - P₁ V₁)

ΔH = 6300 + 2100 = 8400 J

P is a linear function; the average external pressure during a quasi-step between the two states is

P_ext ≈ (400 + 100) / 2 = 250 Pa

Work done W = - P_ext (V₂ - V₁)

W = - 250 (6 - 3) = -750 J

Example 3. 4 moles of an ideal gas (C_V = 15 J K^-1 mol^-1) is subjected to the following process represented on P-T graph. From the given data find out whether the process is isochoric or not; also calculate q, w, ΔU, ΔH.

Solution.

Ideal gas law: PV = nRT

From graph data (substituting numerical values):

4 V = 4 R × 400 ⇒ V = 400 R

3 V = 4 R × 300 ⇒ V = 400 R

Therefore V is constant (isochoric).

w = 0

ΔU = n C_V ΔT

ΔU = 4 × 15 × (400 - 300) = 4 × 15 × 100 = 6000 J

ΔH = n C_P ΔT = n (C_V + R) ΔT

ΔH = 4 × (15 + 8.3) × 100 ≈ 9320 J

Example 4. 2 mole of a gas at 1 bar and 300 K are compressed at constant temperature by use of a constant pressure of 5 bar. How much work is done on the gas?

Solution.

Numerical evaluation gives W = 19953.6 J (work done on the gas is positive in sign convention when we consider work done on the system).

Example 5. 2 moles of an ideal diatomic gas (C_V = 5/2 R) at 300 K, 5 atm expanded irreversibly and adiabatically to a final pressure of 2 atm against a constant pressure of 1 atm.

(1) Calculate final temperature q, w, ΔH & ΔU

(2) Calculate corresponding values if the above process is carried out reversibly.

Solution.

For an adiabatic process q = 0.

w = ΔU = n C_V (T₂ - T₁)

Given: T₁ = 300 K, computed T₂ = 270 K (from the data or relations)

P_ext = 1 atm, P₂ = 2 atm, P₁ = 5 atm

q = 0

w = ΔU = n C_V ΔT = 2 × (5/2 R) × (270 - 300)

Numerical evaluation gives w = ΔU = -1247.1 J

ΔH = n C_P ΔT = n (C_V + R) ΔT

Numerical evaluation gives ΔH = 1745.94 J

If the process is reversible, the adiabatic relation Pv^γ = constant applies and one can find the reversible final temperature from

P^1-γ T^γ = constant

Example 6. 10 g of Helium at 127 °C is expanded isothermally from 100 atm to 1 atm. Calculate the work done when the expansion is carried out:

(i) In single step

(ii) In three steps with intermediate pressures 60 atm and 30 atm respectively

(iii) Reversibly

Solution.

(i) For a one-step (single-step irreversible) expansion the work done equals V ΔP (using constant external pressure over each step formula) - see sketch of calculation below.

(ii) In three steps evaluate work for each step using the volume at the beginning of that step multiplied by the pressure change in that step.

V_I = 83.14 × 10^-5 m³

W_I = 83.14 × 10^-5 × (100 - 60) × 10⁵ = 3325.6 J

W_II = 138.56 × 10^-5 × (60 - 30) × 10⁵ = 4156.99 ≈ 4157 J

W_III = 277.13 × 10^-5 × (30 - 1) × 10⁵ = 8036.86 J

W_total = W_I + W_II + W_III = 3325.6 + 4156.909 + 8036.86 = 15519.45 J

(iii) For the reversible isothermal expansion use W = - nRT ln (V₂ / V₁) - see image for full reversible calculation.

Example 7. Calculate the amount of work done by 2 mole of an ideal gas at 298 K in reversible isothermal expansion from 10 litre to 20 litre.

Solution.

Work for reversible isothermal expansion:

Given n = 2, R = 8.314 J K^-1 mol^-1, T = 298 K, V₁ = 10 L, V₂ = 20 L.

Substitute into W = - nRT ln (V₂ / V₁).

Numerical evaluation gives W = -3,434.9 J (negative sign indicating work done by system).

Example 8. 5 moles of an ideal gas expand isothermally and reversibly from a pressure of 10 atm to 2 atm at 300 K. What is the largest mass which can be lifted through a height of 1 m in this expansion?

Solution.

Work done by the system is W = - nRT ln (P₂ / P₁) (since V ∝ 1/P for isothermal ideal gas). See the image for the explicit work evaluation.

If M is the mass that can be lifted through height h = 1 m, mechanical work required = M g h.

Set mechanical work equal to available thermodynamic work (magnitude):

M g = |W|

Solving numerically with g = 9.8 m s^-2 gives M ≈ 2048.469 kg.

(4) Adiabatic Ideal Gas Expansion & Compression

Definition. An adiabatic process is one in which there is no heat exchange with surroundings: dq = 0.

Therefore dU = dw and ΔU = W (work done on the system produces internal energy change).

For an ideal gas C_P - C_V = R.

Reversible adiabatic ideal gas expansion & compression

For a reversible adiabatic process n C_V dT = - P_int dV (and P_int = P_ext at each step for reversibility).

From integration for an ideal gas we obtain the standard adiabatic relations:

T₂ V₂^γ-1 = T₁ V₁^γ-1

and

T V^γ-1 = constant

Calculation of q, w, ΔH, ΔU for a reversible adiabatic process:

Since dq = 0 ⇒ dU = dw.

For a reversible change the expression for work and internal energy changes follows from substitution of P = nRT / V and integrating along the reversible adiabatic path.

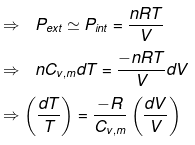
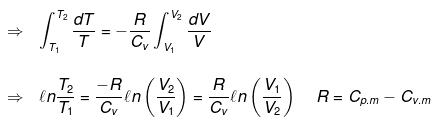
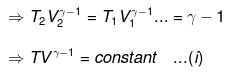
Substituting V = nRT / P where appropriate gives the detailed integrated expressions - see images for full derivation.

Substituting T = P V / nR in equations yields the same adiabatic relations. The equations derived are valid only for reversible adiabatic processes; they cannot be applied directly to irreversible adiabatic processes.

Expression for work:

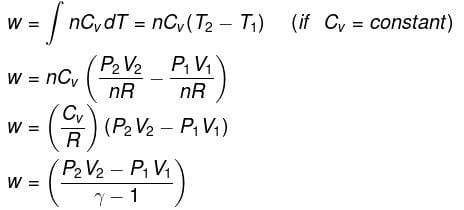
Expression for ΔH and ΔU:

Irreversible adiabatic ideal gas expansion & compression

For an irreversible adiabatic change dq = 0, so dU = dw still holds, but the reversible adiabatic relations (PV^γ = constant etc.) are not valid.

Thus, n C_V (T₂ - T₁) = - P_ext (V₂ - V₁)

Calculation of Q, W, ΔH, ΔU for irreversible adiabatic process involving an ideal gas

Operationally, adiabatic and isothermal irreversible processes share similar judgement criteria: the work depends on the external pressure path and ΔU is calculated by n C_V ΔT.

Examples of irreversible adiabatic changes include sudden removal of partitions or abrupt removal of large amounts of dust that causes rapid expansion.

In an irreversible adiabatic process, heat absorbed q = 0 ⇒ dU = w_irr. (Equation (i))

If P_ext = P₂ = P_final, then the equation for work becomes

Equations (ii) or (iii) (as shown in images) can be solved for T₂ for a given P_ext. The explicit expression for work is shown:

Note. If two states A and B are connected by a reversible path then they cannot in general be connected by an irreversible path with the same path properties. If two states are linked by an adiabatic reversible and an adiabatic irreversible path then comparison of w_rev and w_irrev leads to contradictions if one assumes equality, because internal energy U is a state function and work is a path function.

Therefore ∆U_irrev ≠ ∆U_rev in general when the processes are different; there exists a unique reversible adiabatic path connecting two states (for specified end states), and the numerical values of work and heat depend on the path chosen.

Worked Examples - Adiabatic Processes

Example 1. Two moles of an ideal monoatomic gas at NTP are compressed adiabatically and reversibly to occupy a volume of 4.48 dm³. Calculate the amount of work done, ΔU, final temperature and pressure of the gas. C_V for ideal gas = 12.45 J K^-1 mol^-1.

Solution.

Initial conditions:

V₁ = 2 × 22.4 = 44.8 dm³

P₁ = 1 atm

T₁ = 273 K

Final volume V₂ = 4.48 dm³

Use reversible adiabatic relations: PV^γ = constant and T V^γ-1 = constant.

Compute

or

or

From the algebraic steps and logarithms shown:

P₂ ≈ (10)^1.667 = 46.45 atm

Final temperature from T V^γ-1 = constant yields

T₂ ≈ 1268 K

Work done on the system = n C_V (T₂ - T₁)

W = 2 × 12.45 × (1268 - 273) = 2 × 12.45 × 995 = 24,775.5 J

From first law, ΔE = q + w = 0 + 24,775.5 = 24,775.5 J

Example 2. A certain volume of dry air at NTP is expanded reversibly to four times its volume. Calculate the final pressure and temperature in each case, assuming ideal behaviour.

(C_P / C_V for air = 1.4)

Solution.

Let initial state be at NTP: T₁ = 273 K, P₁ = 1 atm, V₁ = V₁.

(a) Isothermal expansion to four times the volume

For isothermal expansion T₂ = T₁ = 273 K.

Use P₁ V₁ = P₂ V₂ with V₂ = 4 V₁.

(b) Adiabatic expansion to four times the volume

Use PV^γ = constant to determine final P and T for adiabatic case (images show the algebraic steps and final numerical values).

Comparison of Reversible Isothermal and Reversible Adiabatic Ideal Gas Expansion

Expansion

(i) If final volumes are same

Isothermal case: P₁ V₁ = P_iso V₂

Adiabatic case: P₁ V₁^γ = P_adia V₂^γ

From comparison (images):

(ii) If final pressures are same

Isothermal case: P₁ V₁ = P₂ V_iso

Adiabatic case: P₁ V₁^γ = P₂ V_adia^γ

In ideal gas expansion |W_iso| > |W_adia| and consequently

Compression

(i) If final volumes are same

For isothermal compression: P₁ V₁ = P_iso V₂

For adiabatic compression: P₁ V₁^γ = P_adia V₂^γ

(ii) If final pressures are same

P₁ V₁ = P₂ V_iso