Work and Important Concepts | Science Class 9 PDF Download
| Table of contents |

|
| Work |

|
| Not Much ‘work’ In Spite Of Working Hard! |

|
| Scientific Conception of Work |

|
| Work Done by a Constant Force |

|
| Units of Work |

|
| Some Solved Examples |

|
Work
In our day-to-day lives, we often use the term 'work' to describe both mental and physical efforts. However, the concept of work in physics is distinctly different from this everyday understanding. To make this point clear let us consider a few examples.
Not Much ‘work’ In Spite Of Working Hard!
Examples:
- You may read a book or exert yourself mentally in thinking about a simple or difficult problem.
- You might be holding a weight without moving.
- You may be carrying a load and moving with uniform velocity.
- You may be trying hard to move a huge rock that does not move despite your best efforts, though you may get completely exhausted in the process.
In all these cases, according to scientific definition, you are not doing any work. Let's dive into the fascinating world of physics and explore this unique perspective on work!
Scientific Conception of Work
In physics, the term work is used in a special technical sense and has a much more precise definition.In physics, work is the measure of energy transfer that occurs when an object is moved by an external force along a displacement. It is defined as the product of the force acting on the object and the distance it is moved in the direction of the force.
Examples:
- When a box is pushed on a floor by applying a force and it moves through some distance, work is said to be done. In this case, the applied force displaces the box.
- When we pull a trolley by applying a force and it moves through some distance, work is again said to be done.
- When we lift a box through a height, we have to apply force. In this case, the applied force does work in lifting the box.
From all the examples given above, it follows that work is done if:
- Force is applied on the object.
- The object is displaced from its original position.
Note: No work is said to be done if any of the two conditions is not satisfied.
Work Done by a Constant Force
When Constant Force is Acting in the Direction of Displacement
- If a body, A is kept on a smooth horizontal surface, and a force F is applied as shown.
- This force acts on the body for some time during which the displacement of the body is s.
- In such a case, work is defined as follows, work done by a force on a body is the product of force and displacement of the body in the direction of the force.

- Work = Force × Displacement i.e. W = F × s.
- Work is a scalar quantity, i.e. it has no sense of direction.
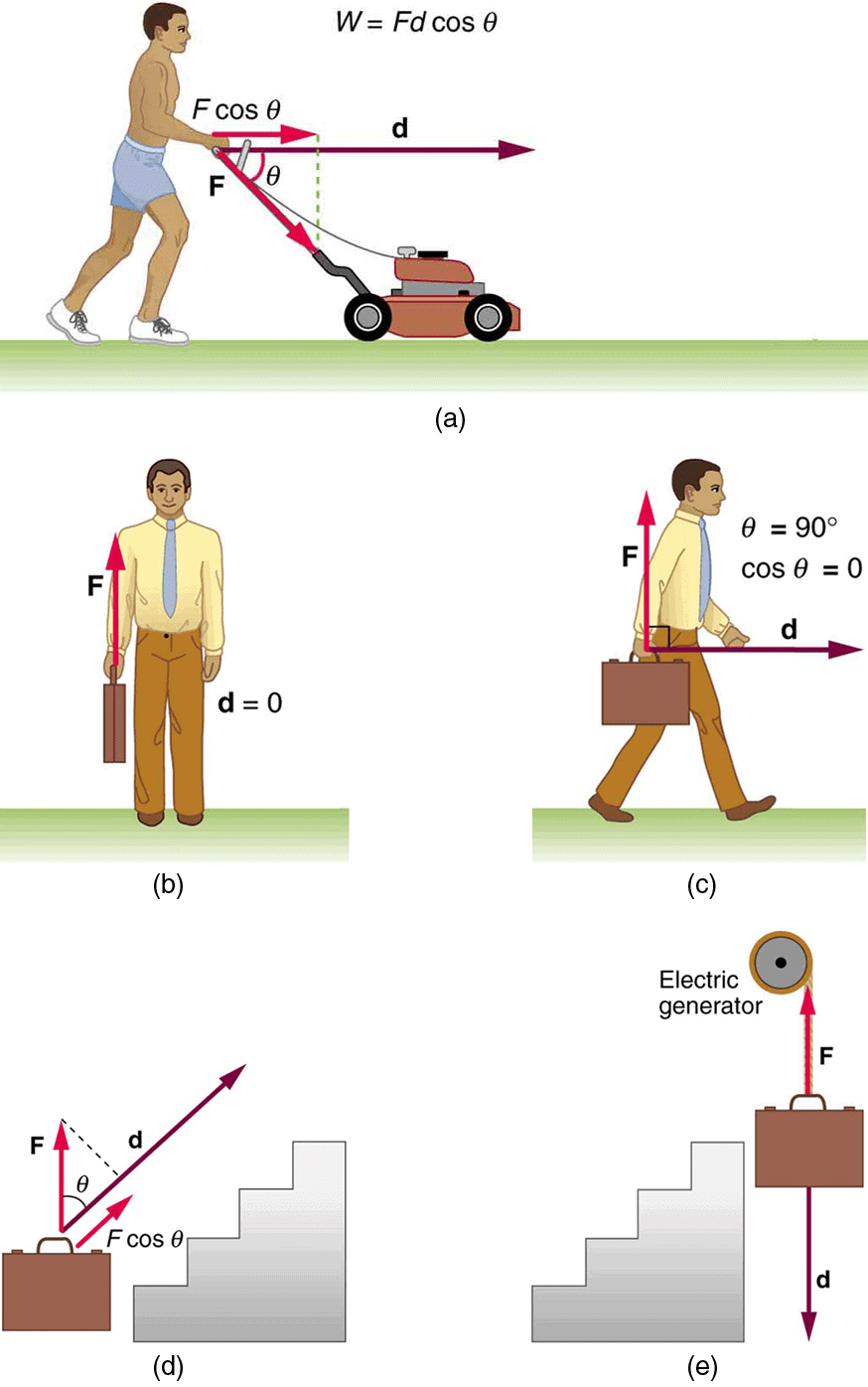
When a Constant Force is Acting at an Angle to the Displacement
- Let us consider body A lying on a smooth horizontal surface. A constant force F acts at an angle θ to the horizontal. The body is displaced through a distance in the horizontal direction.
- Here the complete force F is not responsible to displace the body. A part of the force acting in the direction of displacement is responsible for displacing the body. This horizontal part is F cos θ.
- Work done in this case is defined as 'Work done by a constant force acting at an angle to the displacement is the product of the component of force in the direction of displacement and the displacement of the body'.
- Work = Component of force in the direction of displacement x Displacement,
i.e. W = (F cos θ ) × s ⇒ W = F s cos θ. - Work done is maximum when a force acts in the direction of displacement.
Case-1:
- In W = F s cos θ, Work done is positive when θ is acute. This is because cos θ is positive.
- Work done is maximum when θ = 0°. This is because the maximum value of cos θ = 1.
This happens when a force acts in the direction of displacement.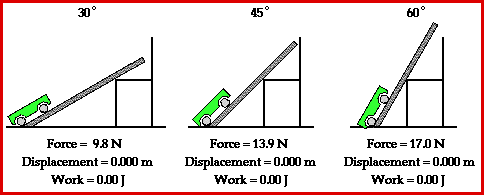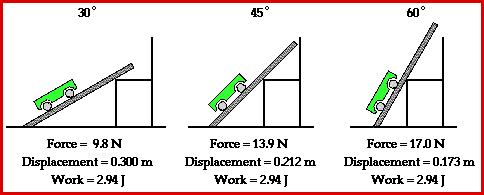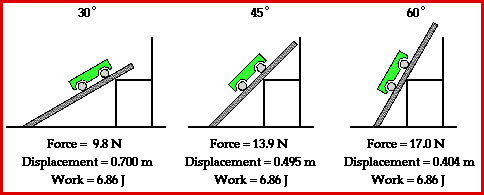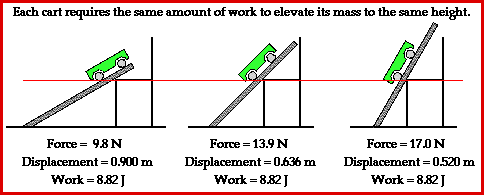
Case-2:
- When the angle between force and displacement is 90°,
i.e. when θ = 90°, then cos 90° = 0. - In this case, work done is zero.
- Work done by centripetal force
When a stone is whirled in a horizontal circle, the centripetal force acts at 90° to the displacement. Therefore, work done by the centripetal force is zero. - Work done by coolie
When a coolie moves on a horizontal surface, he applies a force on the load kept on his head in the vertically upward direction. Therefore, θ = 90°. Therefore, work done by the force applied by coolie is zero. - The motion of the Earth around the Sun
Work done by the centripetal force (which is the gravitational pull of the sun on earth) acting on earth is zero. Because centripetal force is perpendicular to the displacement. [Remember the displacement is always tangential and centripetal force is always radially inward. The angle between radius and tangent is 90°].
 Work done in Various Situations
Work done in Various Situations
Case-3:
When the angle between force and displacement is 180°,
i.e. when θ =180° then cos 180° = -1.
In this case, work done is negative.
Example: A block A is pushed by the force F and displaced through a distance s.
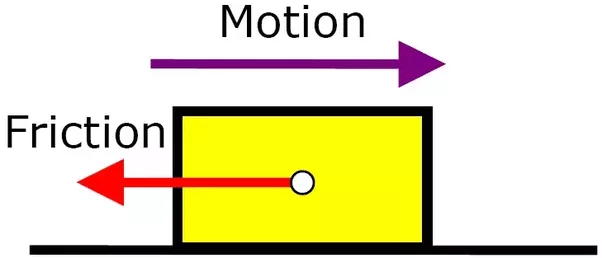 Work Done by Friction is Negative
Work Done by Friction is Negative
- Work done by the applied force,
W = F × s × cos 0° = Fs. - Work done by frictional force,
W = f × s × cos 180° = – fs.
Units of Work
In CGS system:
- Unit of work = erg.
- When a force of 1N acts on an object and the object moves a distance of 1cm in the direction of the force, the work done by the force is 1erg.
- 1erg = 1 dyne × 1 cm.
In SI system:
- Unit of work = joule(J).
- When a force of 1N acts on an object and the object moves a distance of 1m in the direction of the force, the work done by the force is 1J.
- 1J = 1 N x 1 m.
Definition of One Joule
When F = 1N, s = 1m, then W = 1J.
If a displacement of 1m is produced by a force of 1N acting in the direction of displacement then the work done by the force is 1J.
1J= 1 N x 1 m = 105 dyne × 102 cm = 107 erg
Some Solved Examples
Example 1:
Imagine you are pushing a 10 kg box across a smooth, flat floor. You are applying a force of 20 N at an angle of 30° above the horizontal direction. The box moves 5 meters to the right. Calculate the work done on the box.
Solution: In this situation, the displacement is in the horizontal direction (5 meters to the right), and the force has a horizontal component as well as a vertical component. To find the work done, we only need to consider the horizontal component of the force, which is given by Fx = F * cos θ, where F is the applied force and θ is the angle between the force and the displacement.
Fx = 20 N * cos(30°) = 20 N * (√3 / 2) = 10√3 N
Now, we can calculate the work done using the formula W = Fx * d, where d is the displacement.
W = 10√3 N * 5 m = 50√3 J
Thus, the work done on the box is 50√3 Joules. Since the angle is acute (30°), the work done is positive, and since the force has a component in the direction of the displacement, the work done is maximum.
Example 2:
A coolie carries a load of 50 kg on his head and walks along a horizontal surface. He applies a force on the load in the vertically upward direction. He walks a distance of 100 meters. Calculate the work done by the coolie on the load.
Solution:
Given,
Mass of load = 50 kg
Distance traveled = 100 m
The force applied by the coolie is in the vertically upward direction, and the displacement of the load is in the horizontal direction. Therefore, the angle between the force and the displacement, θ = 90°.
We know that work done, W = F × d × cos θ
Since θ = 90°, cos 90° = 0.
Hence, work done, W = F × d × 0 = 0
Thus, the work done by the coolie on the load is 0 Joules.
Example 3:
A person pushes a 10 kg block with a force of 50 N along a horizontal surface for a distance of 4 meters. The frictional force acting on the block is 30 N. Calculate the work done by the applied force and the work done by the frictional force.
Solution:
Given:
Mass of the block, m = 10 kg
Applied force, F = 50 N
Distance, s = 4 m
Frictional force, f = 30 N
First, let's find the work done by the applied force:
Wapplied = F × s × cos 0°
Wapplied = 50 N × 4 m × 1 (since cos 0° = 1)
Wapplied = 200 J (Joules)
Now, let's find the work done by the frictional force:
Wfriction = f × s × cos 180°
Wfriction = 30 N × 4 m × (-1) (since cos 180° = -1)
Wfriction = -120 J (Joules)
So, the work done by the applied force is 200 J, and the work done by the frictional force is -120 J.
|
84 videos|478 docs|60 tests
|
FAQs on Work and Important Concepts - Science Class 9
| 1. What is the scientific conception of work? |  |
| 2. How is work done by a constant force calculated? |  |
| 3. What are the units of work? |  |
| 4. Can you provide some examples of work? |  |
| 5. What are some important concepts related to work? |  |





















