Worksheet Solutions: Index Numbers | Economics Class 11 - Commerce PDF Download
| Table of contents |

|
| Assertion-Reasoning based MCQs |

|
| Read the following case study graph and answer the question |

|
| Short Answer Type Questions |

|
| Long Answer Type Questions |

|
Multiple Choice Questions
Q1: An index number which accounts for the relative importance of the items is known as
(a) Weighted index
(b) Simple aggregative index
(c) Simple average of relatives
(d) None of the above
Ans: (a)
Q2: The ...... value of index number is a pure number.
(a) average
(b) commodity
(c) price relative
(d) All of these
Ans: (c)
Q3: The item having the highest weight in consumer price index for industrial workers is
(a) food
(b) housing
(c) clothing
(d) None of these
Ans: (a)
Q4: Index numbers are very helpful in comparing the economic conditions of a particular group of people for ____ different periods.
(a) three
(b) two
(c) four
(d) None of these
Ans: (b)
Q5: In general, inflation is calculated by using
(a) Wholesale Price Index
(b) Consumer Price Index
(c) Producer’s Price Index
(d) None of these
Ans: (a)
Q6: Which of the following devices is used for measuring differences in the magnitude of a group of related variables?
(a) Arithmetic mean
(b) Index number
(c) Correlation
(d) Mode
Ans: (b)
Q7: The impact of change in the price of a commodity with little weight in the index will be
(a) small
(b) large
(c) uncertain
(d) None of these
Ans: (a)
Q8: Statement I An appropriate method for working out consumer price index is family budget method.
Statement II Index numbers are devices for measuring differences in the magnitude of a group of related variables.
Alternatives
(a) Statement I is correct and Statement II is incorrect
(b) Statement II is correct and Statement I is incorrect
(c) Both the statements are correct
(d) Both the statements are incorrect
Ans: (c)
Q9: In most of the weighted index numbers the weight pertains to
(a) base year
(b) current year
(c) both base and current year
(d) None of these
Ans: (a)
Q10: Which of the following index numbers is based on the assumption that all the commodities are of equal importance?
(a) Weighted index number
(b) Simple index number
(c) Both (a) and (b)
(d) None of these
Ans: (c)
Q11: Statement I Construction of index numbers only needs choosing commodity basket.
Statement II Index numbers have universal acceptance.
Alternatives
(a) Statement I is correct and Statement II is incorrect
(b) Statement II is correct and Statement I is incorrect
(c) Both the statements are correct
(d) Both the statements are incorrect
Ans: (b)
Q12: If Laspeyre’s index is 110 and Paasche’s index is 108, fisher’s index will be
(a) 100
(b) 108
(c) 109
(d) None of these
Ans: (c)
Q13: In Laspeyre’s index number, the weight pertains to
(a) base year quantities
(b) current year
(c) Both (a) and (b)
(d) None of these
Ans: (a)
Q14: Choose the correct pair. 
Codes
(a) A–(i)
(b) B–(ii)
(c) C–(iii)
(d) None of these
Ans: (c)
Q15: Factor Reversal Test is expressed in terms of
(a) ∑P1Q1/∑P0Q0
(b) ∑P1Q0/∑P0Q0/∑P1Q1/∑P0Q1
(c) ∑P1Q1/∑Q0P1
(d) ∑Q1P0/∑Q0P0 X∑P1Q1/∑Q0P1
Ans: (d)
Assertion-Reasoning based MCQs
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A)
(c) Assertion (A) is true, but Reason (R) is false
(d) Assertion (A) is false, but Reason (R) is true
Q1: Assertion (A) Index number serves as the barometer for measuring the value of money in an economy.
Reason (R) Index numbers have universal acceptance thus can be applied in any case.
Ans: (b)
Q2: Assertion (A) A better way to estimate GDP accurately is to deflate input and output prices through separate indices.
Reason (R) When output prices move relatively faster than the input prices, the single deflation method overestimates GDP.
Ans: (a)
Q3: Assertion (A) Value index is based upon both price and quantity.
Reason (R) Value is calculated by the product of price and quantity.
Ans: (b)
Q4: Assertion (A) Wholesale price index is used to measure the changes in the prices of goods that impacts individual.
Reason (R) Positive value of index number indicates rise in general price levels.
Ans: (d)
Q5: Assertion (A) Fisher’s method of index number is considered as ideal weighted method of index numbers.
Reason (R) Fisher’s method passes all statistical tests of time and factor reversal.
Ans: (a)
Read the following case study graph and answer the question
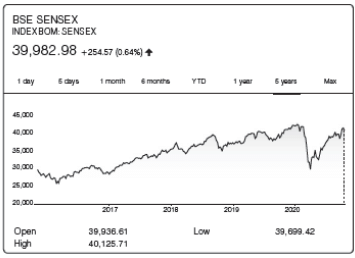
Q6: As per the given graph, rising Sensex indicates ………… .
(a) growth of economy
(b) growth of investors profit
(c) inflow of foreign currency
(d) All of the above
Ans: (b)
Q7: Which year shows a decrease in stock price as per the given graph?
(a) 2017
(b) 2018
(c) 2019
(d) 2020
Ans: (d)
Q8: Which year is considered as the base year for constructing Sensex in India?
(a) 1978-79
(b) 2000-01
(c) 2004-05
(d) 2011-12
Ans: (a)
Q9: ____ type of average is used to calculate the value of index number.
(a) Simple
(b) Weighted
(c) Proportionate
(d) Both (a) and (b)
Ans: (b)
Q10: Index number is always expressed in terms of ____
(a) percentage
(b) proportionate
(c) Both (a) and (b)
(d) None of these
Ans: (a)
Q11: The given graph shows 0.64% increase, what does it indicate?
(a) Rise in number of stocks
(b) Rise in stock prices
(c) Fall in stock price
(d) None of these
Ans: (b)
Direction Read the following case study and answer the question no. (i) to (vi) on the basis of the same.
We frequently see index numbers, such as the Consumer Price Index (CPI), in our daily life.
Economists often use the index numbers to compare values measured at different points in time. Using an index can make quick comparisons
easy. The index numbers have become a widely accepted statistical device for measuring business activity changes. A typical use of the index number technique in business is to summarize complex situations with a single performance index so that a dashboard (or report) would have enough space to show all KPIs. An index number is used to measure changes in the magnitude of a variable or group of variables regarding time,geographical location, or other characteristics such as profession.
IT professionals who need to analyse economic and business activities, but have limited experience in statistics, want to learn how to construct and interpret performance indexes. Index numbers are also not free from criticism as its base year and commodity selection requires a lot of attention and expert attention.
Q12: Choose the correct statement from given below
(a) Index numbers are cent percent accurate
(b) There is null possibility of biasness in case of index numbers
(c) Index number is based upon all the items given in the data
(d) All of the above
Ans: (c)
Q13: Which of the following problems comes in the construction of index numbers?
(a) Selection of base year
(b) Selection of commodities
(c) Selection of quantities
(d) All of these
Ans: (d)
Q14: Index numbers can be used in which of the following fields?
(a) Geographical areas
(b) Change in magnitude of a variable
(c) Change in time periods
(d) All of the above
Ans: (d)
Q15: Application of index numbers which is based on data related to different time period is known as ____ .
(a) Time series data
(b) Temporal data
(c) Inter-temporal data
(d) All of these
Ans: (d)
Q16: Assertion (A) Selection of incorrect base leads to mis-leading conclusion.
Reason (R) A year with high fluctuations in prices should not be considered as base year.
Alternatives
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A)
(c) Assertion (A) is true, but Reason (R) is false
(d) Both are false
Ans: (a)
Q17: Economists often use the index numbers to ...........values measured at different points in time.
(a) measure
(b) change
(c) compare
(d) All of these
Ans: (a)
Short Answer Type Questions
Q1: Is the change in any price reflected in a price index number?
Ans: No, the change in any price is not reflected in a price index number. Price index numbers measure and permit comparison of the prices of certain goods included in the basket being used to compare prices in the base period with prices in the current period. Moreover, an equal rise in the price of an item with large weight and that of an item with low weight will have different implications for the overall change in the price index.
Q2: Why do we need an index number?
Ans: Index numbers are needed because of the various advantages which pertain to the use of index numbers.
These advantages
(i) Barometer of Economic Progress Index numbers are a barometer for measuring the value of money and assessing the level of economic progress.
(ii) Importance for the Government The government adopts suitable monetary and fiscal policies according to the changes in index numbers.
(iii) Throws Light on Economic Condition Index numbers are very helpful in comparing the economic condition of a particular group of people across two time periods.
(iv) Fixation of Wages of Policy-making Index numbers such as CPI and WPI help the government and executives for the fixation and revision of wages.
Q3: What are the desirable properties of the base period?
Ans: Base period should have the following properties
(i) The base year should be a normal year in which extraordinary events such as earthquake, flood, war, elections, etc should not have occurred.
(ii) The period should not be too far in the past as comparison cannot be done with such a base year because policies, economic and social conditions change with time.
(iii) Base period should be updated periodically.
Thus, we can conclude that while selecting base period, certain factors should be considered.
Q4: If the salary of a person in the base year is ₹4,000 per annum and the current year salary is ₹6,000, by how much should his salary rise to maintain the same standard of living, if the CPI is 400?
Ans: Base year salary =₹4,000, Base year index = 100 (assumption), Current year index = 400 Salary required in the current year to maintain the same standard of living of base year = Base Year Salary × CPI of Current Year CPI of Base Year = 4 000 × 400 100 , = ₹16,000 Current year salary = ₹6,000 The increase in current salary required = 16,000 − 6,000 = ₹10,000
Q5: What is the difference between a price index and a quantity index?
Ans: The differences between a price index and a quantity index are as follows (i) Price index numbers measure and allow for comparison of the prices of certain goods while quantity index numbers measure the changes in thephysical volume of production, construction or employment.
(ii) Price index numbers are more widely used as compared to quantity index numbers.
(iii) Quantity index does not indicate the real change in the purchasing power of money while price index does.
Q6: Give the limitations of simple aggregative method of computing index number.
Ans: Although computation of index number is quite simple while using this method, yet it is not ordinarily used because of the following limitations
(i) All items are given equal weightage.
(ii) This measure of index number is influenced by the items which are highly priced.
(iii) This method is affected with the change in the unit of measurement.
For example, index number computed when price of wheat is expressed in per kg, will be different from the index number computed when the price of wheat is expressed in per quintal.
Q7: Which method is considered ‘ideal’ for constructing index number and why?
Ans: Fisher’s method is considered ideal for constructing index number because
(i) It satisfies factor reversal test.
(ii) It satisfies time reversal test.
(iii) It is based on different weights.
Q8: Mr Ashok was getting ₹ 400 in the base year and ₹ 800 in the current year. If Consumer Price Index is ₹ 350, then what extra amount is required for maintaining the earlier standard of living?
Ans: For former standard of living, Ashok should get = Salary in Base Year × CPI 100 = × = 400 350 100 1,400 \ Amount required for maintaining the same standard of living = 1,400 − 800 = ₹600
Q9: Explain briefly the process of data collection for Consumer Price Index (CPI).
Ans: Primary data is collected every month to compute rural and urban CPI in the following ways
(i) For CPI (Rural), two villages are selected from each district. Presently data is collected from 1,181 villages. Number of items for price data collection is identified through the market survey and it is around 225. Price data is collected from selected shops in the villages every month by the Department of Posts.
(ii) For CPI (Urban), data is collected from all cities, having a population of more than 9 lakhs. Presently, total number of selected cities is 310. Number of items for price data collection is identified through the market survey and it is around 250. Each selected market is visited every month for price data collection from shops and outlets.
(iii) 4.75 lakh price data records collected from rural and urban areas are uploaded per month to the web portal of National Informatics Centre, which is the formal data collection arm of NSSO (National Sample Survey Organisation).
Long Answer Type Questions
Q1: Discuss in brief, the methods of constructing weighted index numbers.
Ans: Weighted index numbers are the index number in which different items of the series are accorded different weightage, depending upon their relative importance.
There are two methods of constructing weighted index numbers
(i) Weighted Average of Price Relative Method According to this method, weighted index number is simply the weighted arithmetic mean of price relative. In this method, weighted sum of the price relative is divided by the sum total of the weights.
Thus, P01= [∑/W/∑W]
(ii) Weighted Aggregative Method Under this method,weights are assigned to various items and instead of finding the simple aggregate of price, the weighted aggregate of the price are obtained. The different methods to compute weighted aggregative index numbers are
Laspeyre’s Method This method uses the base year quantities as weights.
The following formula is used to calculate index number
P01 = ∑P1q0/∑poq0x100
Paasche’s Method This method uses the current year quantities as weights The following formula is used to calculate index number
p01= ∑P1q1/∑poq1x100
Fisher’s Method This method combines the techniques of Laspeyre’s method and Paasche’s method and uses both base year as well as current year quantities (q0 ,q1 ) as weight. The formula to construct index number is p01= √∑P1q0/∑P0q0 x∑P1q1/∑P0q1 x 100
Q2: Explain briefly the various characteristics or features of index numbers.
Ans: The characteristics of index numbers are as follows
(i) Specialised Averages Index numbers are specialised averages as they are helpful in computing combined averages of goods and services expressed in different units. Unlike the measures of central tendency, which can compute averages of variables expressed in one unit only, index numbers can measure the averages of variables with diverse units.
(ii) Measure the Relative Changes Index numbers measure the relative change in the value of the variable under study. Because of this, index numbers are expressed in terms of percentage which are independent of the units of measurement.
(iii) Measure the Net Changes Index numbers measure net changes in a variable or group of variables. They describe net change in a single number. This facilitates the comparisons of two or more index numbers.
(iv) Measure the Change not Capable of Direct Measurement Index numbers are meant to study the changes in the effects of such factors which cannot be measured directly. For example, changes in business activity in a country are not capable of direct measurement but it is possible to study relative changes in business activity with the help of index number.
|
59 videos|222 docs|43 tests
|
FAQs on Worksheet Solutions: Index Numbers - Economics Class 11 - Commerce
| 1. What is the purpose of using assertion-reasoning based multiple-choice questions (MCQs) in exams? |  |
| 2. How are assertion-reasoning based MCQs different from traditional multiple-choice questions? |  |
| 3. What are the benefits of using assertion-reasoning based MCQs in exams? |  |
| 4. How can students effectively answer assertion-reasoning based MCQs? |  |
| 5. How can educators incorporate assertion-reasoning based MCQs in their teaching methodologies? |  |



















