Worksheet Solutions: The Other Side of Zero - 1 | Worksheets with Solutions for Class 6 PDF Download
| Table of contents |

|
| Multiple Choice Questions (MCQs) |

|
| Fill in the Blanks |

|
| True/False |

|
| Practical Application Questions |

|
| Word problems |

|
Multiple Choice Questions (MCQs)
Q1: What is the result of (-5) + (+3)?
(a) -8
(b) 2
(c) -2
(d) 8
Ans: (c) -2
Solution: Adding -5 and +3 results in -2 because you're moving 3 units to the right from -5.
Q2: Which of the following represents the correct inverse operation for subtracting -4?
(a) Adding +4
(b) Subtracting +4
(c) Adding -4
(d) None of the above
Ans: (a) Adding +4
Solution: Subtracting -4 is the same as adding +4.
Q3: What is the value of the expression (-6) - (-3)?
(a) -9
(b) -3
(c) -1
(d) -2
Ans: (b) -3
Solution: Subtracting -3 from -6 is the same as adding +3, which gives -3.
Q4: If you move 7 steps to the left from +2 on a number line, where will you end up?
(a) -5
(b) 5
(c) 9
(d) -9
Ans: (a) -5
Solution: Moving 7 steps left from +2 lands you at -5.
Q5: The sum of -7 and -3 is closest to which of the following?
(a) -10
(b) 10
(c) -4
(d) 4
Ans: (a) -10
Solution: Adding -7 and -3 results in -10.
Fill in the Blanks
Q1: The number line extends infinitely in both directions, with positive numbers on the right of 0 and _______ numbers on the left.
Ans: Negative
Solution: Negative numbers are those less than zero and are represented to the left of 0 on the number line.
Q2: The additive inverse of +7 is _______.
Ans: -7
Solution: The additive inverse of a number is what you add to it to get zero. For +7, the additive inverse is -7.
Q3: When you subtract a negative number, it is the same as _______ the corresponding positive number.
Ans: Adding
Solution: Subtracting a negative number is equivalent to adding the positive counterpart of that number.
Q4: On a number line, moving to the left signifies _______, while moving to the right signifies _______.
Ans: Subtraction, Addition
Solution: Moving left on the number line decreases the value (subtraction), while moving right increases it (addition).
Q5: The sum of a number and its inverse is always _______.
Ans: Zero
Solution: Adding a number to its additive inverse results in zero.
True/False
Q1: The number zero is considered neither positive nor negative.
Ans: True
Solution: Zero is neutral, lying between positive and negative numbers on the number line.
Q2: The number -5 is greater than the number -3.
Ans: False
Solution: On the number line, -5 is to the left of -3, making it smaller.
Q3: Subtracting a positive number is the same as adding its inverse.
Ans: True
Solution: Subtracting a positive number reduces the value, equivalent to adding its negative counterpart.
Q4: If you add two negative numbers, the result is always positive.
Ans: False
Solution: Adding two negative numbers gives a negative result.
Q5: On the number line, -1 is closer to zero than -2.
Ans: True
Solution: The number -1 is closer to zero on the number line than -2.
Practical Application Questions
Q1: Draw a number line and mark the points -3, 0, and +4. Indicate the position you will reach if you move 5 units to the right from -3.
Ans:
Step 1: First, let's draw a number line. A number line is like a ruler, but it can go into negative numbers too. Label the numbers from -5 on the left to +5 on the right.
Step 2: Mark the points -3, 0, and +4 on the number line. To do this:
- Start at 0 in the middle.
- Move 3 steps to the left of 0 to reach -3.
- Stay at 0.
- Move 4 steps to the right of 0 to reach +4.

Step 3: Now, if we start at -3 and move 5 steps to the right, let's see where we land:
- Start at -3.
- Move 1 step to the right to reach -2.
- Move another step to reach -1.
- Keep moving right to 0, +1, and finally +2.
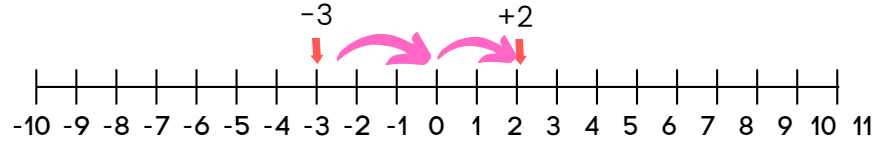
The final position is +2.
Solution: When you move 5 steps to the right from -3, you pass through -2, -1, 0, +1, and land on +2. Moving right means you are adding, so -3 + 5 equals +2.
Q2: Subtract -8 from +3 using a number line. Show the process and the final result.
Ans:
Step 1: Start by drawing a number line and label it from -10 on the left to +10 on the right.
Step 2: Place yourself at +3 on the number line. Now, you need to subtract -8. Subtracting a negative number is like adding its positive counterpart. So instead of moving left, you move to the right.
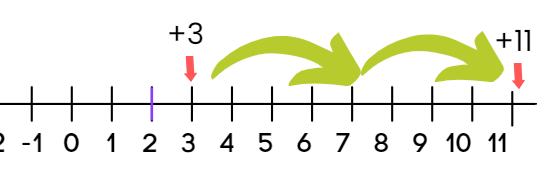
Step 3: Starting at +3, move 8 steps to the right:
- Move from +3 to +4, +5, +6, +7, +8, +9, +10, and finally +11.
The result is +11.
Solution: When you subtract -8 from +3, you’re actually adding 8, because subtracting a negative is like adding the positive version. So +3 - (-8) = +3 + 8 = +11.
Word problems
Q1. A lift in a building starts at the 7th floor.
A) The lift moves down 5 floors. What floor does it reach?
B) From that floor, the lift moves up 3 floors. Where is the lift now?
C) Finally, the lift moves down 4 floors. What floor does it stop at?
Ans:
A) After moving down 5 floors:
7−5=2
The lift is on the 2nd floor.
B) After moving up 3 floors:
The lift is now on the 5th floor.
C) After moving down 4 floors:
The lift is on the 1st floor.
Q2. In a bank, the balance of an account is recorded.
A) John has a balance of ₹500 in his account. He withdraws ₹200. What is his new balance?
B) Then, he deposits ₹150 into his account. What is his balance now?
C) After that, he withdraws ₹100. What is his final balance?
Ans:
A) After withdrawing ₹200:
500−200=300
John's new balance is ₹300.
B) After depositing ₹150:
300+150=450
John's balance is now ₹450.
C) After withdrawing ₹100:
450−100=350
John's final balance is ₹350.
Q3. A miner is working in a mineshaft where the surface level is represented by 0 meters.
A. The miner starts at -10 meters below the surface and then descends 5 meters further. What is his new depth?
B. After that, the miner ascends 8 meters. What is his new depth now?
C. Finally, the miner descends 3 meters. Where is he now?
Ans:
A. After descending 5 meters from -10 meters:
−10−5=−15
The miner is now at -15 meters.
B. After ascending 8 meters:
−15+8=−7
The miner is now at -7 meters.
C. After descending 3 meters:
−7−3 = −10
The miner is now at -10 meters.
FAQs on Worksheet Solutions: The Other Side of Zero - 1 - Worksheets with Solutions for Class 6
| 1. What topics are typically covered in the "Other Side of Zero" exam? |  |
| 2. How can I effectively prepare for the "Other Side of Zero" exam? |  |
| 3. What types of word problems should I expect in the "Other Side of Zero" exam? |  |
| 4. Are there any common mistakes to avoid when working with negative numbers? |  |
| 5. Can I find practice worksheets for the "Other Side of Zero" exam online? |  |
















