X-Ray Diffraction and Bragg’s Law | Physical Chemistry PDF Download
X-rays in Diffraction: X-rays have wavelengths on the order of a few angstroms (1 Angstrom = 0.1 nm). This is the typical inter-atomic distance in crystalline solids, making X-rays the correct order of magnitude for diffraction of atoms of crystalline materials.
How are Diffractions Patterns Made?
When X-rays are scattered from a crystalline solid they can constructively interfere, producing a diffracted beam. Interference occurs among the waves scattered by the atoms when crystalline solids are exposed to X-rays. There are two types of interference depending on how the waves overlap one another.
- Constructive interference occurs when the waves are moving in phase with each other.
- Destructive interference occurs when the waves are out of phase.
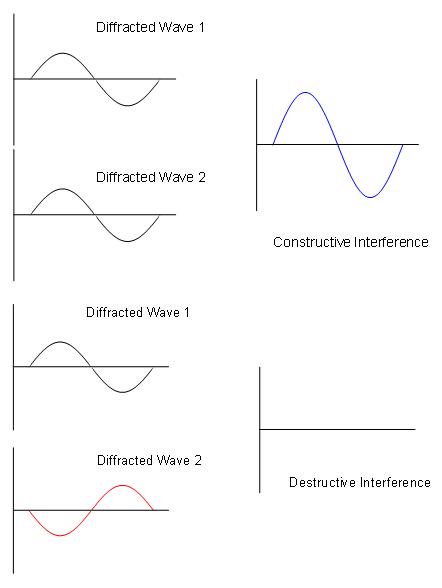
This constructive interference results in diffraction patterns.
What is Bragg’s Law?
Bragg’s law is a special case of Laue diffraction, which determines the angles of coherent and incoherent scattering from a crystal lattice. When X-rays are incident on a particular atom, they make an electronic cloud move like an electromagnetic wave. The movement of these charges radiates waves again with similar frequency, slightly blurred due to different effects, and this phenomenon is known as Rayleigh scattering. Basically, the law explains the relationship between an x-ray light shooting and its reflection off from a crystal surface.
Brag’s Law states the following:
When the X-ray is incident onto a crystal surface, its angle of incidence, θ, will reflect with the same angle of scattering, θ. And, when the path difference, d is equal to a whole number, n, of wavelength, constructive interference will occur.
The exact process takes place upon scattering neutron waves via nuclei or a coherent spin interaction with an isolated electron. These wavefields that are re-emitted interfere with each other destructively or constructively, creating a diffraction pattern on a film or detector. The diffraction analysis is the resulting wave interference, and this analysis is known as Bragg diffraction.
Bragg Equation
According to Bragg Equation:
nλ = 2d sinΘ
Therefore, according to the derivation of Bragg’s Law:
- The equation explains why the faces of crystals reflect X-ray beams at particular angles of incidence (Θ, λ).
- The variable d indicates the distance between the atomic layers, and the variable Lambda specifies the wavelength of the incident X-ray beam.
- n as an integer.
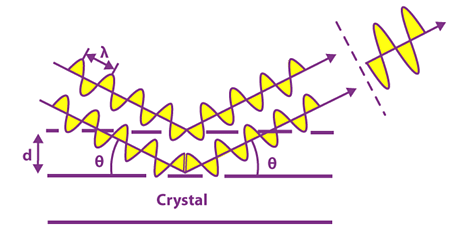
This observation illustrates the X-ray wave interface, called X-ray diffraction (XRD) and proof for the atomic structure of crystals.
Bragg was also awarded Nobel Prize in Physics in identifying crystal structures starting with NaCl, ZnS, and diamond. In addition, to understand the structure of every state of matter by any beam, e.g., ions, protons, electrons, neutrons, with a wavelength similar to the length between the molecular structures, diffraction was developed.
Derivation of Bragg’s Law
Consider the following figure of beams in which the phases of the beams coincide when the incident angle is equal to the reflecting angle. The incident beams are parallel to each other until they reach point z. When they are at point z, they strike the surface and travel upwards. At point B, the second beam scatters. AB + BC is the distance travelled by the second beam. The extra distance is known as the integral multiple of the wavelength.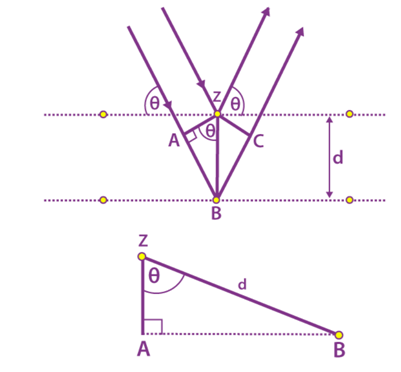
nλ = AB + BC
We also know that AB = BC
nλ = 2AB (equation 1)
d is the hypotenuse of the right triangle Abz. Ab is the opposite of the angle θ.
AB = d sinθ (equation 2)
Substituting equation 2 in equation 1
nλ = 2d sinθ
Applications of Bragg’s Law
There are numerous applications of Bragg’s law in the field of science. Some common applications are given in the points below.
- In the case of XRF (X-ray fluorescence spectroscopy) or WDS (Wavelength Dispersive Spectrometry), crystals of known d-spacings are used as analyzing crystals in the spectrometer.
- In XRD (X-ray diffraction) the inter-planar spacing or d-spacing of a crystal is used for characterization and identification purposes.
Bragg’s Diffraction
Bragg’s diffraction was first proposed by William Henry Bragg and William Lawrence Bragg, in 1913. Bragg’s diffraction occurs when a subatomic particle or electromagnetic radiation, waves have wavelengths that are comparable to atomic spacing in a crystal lattice.
Solved Examples
Example 1: The wavelength of the X-rays is 0.071 nm which is diffracted by a plane of salt with 0.28 nm as the lattice constant. Determine the glancing angle for the second-order diffraction. Assume the value of the salt plane to be 110, and the given salt is rock salt.
Solution: Given:
Wavelength of the X-rays = 0.071 nm
Lattice constant = 0.28 nm
Plane = 110
Order of diffraction = 2
Glancing angle =?
Using Bragg’s law:
2d sin Ө = nλ
Rock salt has FCC, therefore, 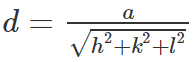
Substituting the values,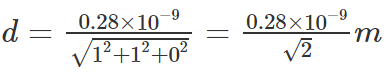
Substituting in the Bragg’s equation,
Ө = 21°
Example 2: The wavelengths of first-order X-rays are 2.20A0 at 2708’. Find the distance between the adjacent Miller planes.
Solution: Using Bragg’s law,
2d sin Ө = nλ
Where,
n = 1
λ = 2.29 A°
Ө = 27°8’
Substituting the values, we get
d = 2.51 A°
Bragg’s law Conclusion
The concluding ideas from Bragg’s law are:
- The diffraction has three parameters i.e, the wavelength of X rays,λ
- The crystal orientation defined by the angle θ
- The spacing of the crystal planes, d.
The diffraction can be conspired to occur for a given wavelength and set of planes. For instance, changing the orientation continuously, i.e., changing theta until Bragg’s Law is satisfied.
Frequently Asked Questions
What is Bragg’s Law?
When the X-ray is incident onto a crystal surface, its angle of incidence, θ, will reflect with the same angle of scattering, θ. And, when the path difference, d is equal to a whole number, n, of wavelength, constructive interference will occur.
What does Bragg’s Law tell us?
Bragg’s law explains the relationship between an x-ray light shooting into and its reflection off from a crystal surface.
Why is Bragg’s Law important?
The Bragg law is useful for measuring wavelengths and for determining the lattice spacings of crystals.
What are the applications of Bragg’s Law?
In the case of XRF (X-ray fluorescence spectroscopy) or WDS (Wavelength Dispersive Spectrometry), crystals of known d-spacings are used as analyzing crystals in the spectrometer.
Bragg’s law experiment is based on which scattering of waves?
Bragg’s law experiment is based on the Rayleigh scattering in which the charges are scattered without a change in their wavelength.
|
83 videos|142 docs|67 tests
|
FAQs on X-Ray Diffraction and Bragg’s Law - Physical Chemistry
| 1. What is the formula for Bragg's Law? |  |
| 2. How is Bragg's Law used in X-ray crystallography? |  |
| 3. What is the significance of the integer 'n' in Bragg's Law? |  |
| 4. How does Bragg's Law help determine the crystal structure? |  |
| 5. Can Bragg's Law be applied to other types of waves besides X-rays? |  |

|
Explore Courses for Chemistry exam
|

|

















