MCQ - Simple and Compound Interest - 1 (Solutions) - CA Foundation PDF Download

Clear all your CA Foundation doubts with EduRev Join for Free

Join for Free

Questions Related to Simple Interest

Ans.1: (c)
Solution: A sum of money at Simple Interest amounts to Rs. 815 in 3 years and Rs. 854 in 4 years
Simple interest for 1 year = 854 – 815 = Rs. 39
⇒ Simple interest for 3 year = 39 × 3 = 117
⇒ The sum is = 815 – 117 = Rs. 698

Ans.2: (a)
Solution: Given: 
Total principal = Rs. 13900
Rate of interest = 14% and 11%
Time = 2 years
Interest = Rs. 3508
Formula Used:
S.I = Principal × rate × time/100
Calculation: 
Let the amount invested in scheme B be Rs 100x.
Amount invested in scheme A = Rs (13900 – 100x)
Rate of interest in scheme A = 14%
Rate of interest in scheme B = 11%
Time = 2 years
Amount of interest earned from scheme A = (13900 – 100x) × 14 × 2/100 = 3892 – 28x
Amount of interest earned from scheme B = 100x × 11 × 2/100 = 22x
According to the question,
⇒ 3892 – 28x + 22x = 3508
⇒ 6x = 384
⇒ x = 64
Amount in scheme B = 100 × 64 = 6400
∴ Amount invested in scheme B = 100 × 64 = Rs 6400

Ans.3: (d)
Solution: By the formula of Simple interest, we know,
S.I. = (Principal x Rate x Time)/100
Principal = (S.I. x 100)/(Rate x Time)
P = (100×4016.25)/9 x 5
P = Rs. 8925.

Ans.4: (b)
Solution: Principal = Rs. 450, R = 4.5%,
S.I. = Rs. 81
S.I = P × R × T/100
T = (SI × 100)/(P × R)
T = (81 × 100)/(450 × 4.5)
∴ T = 4 years

Ans.5: (b)
Solution: As the rate of interest is same as the time for which money is invested
So,
Let rate = R% and time = T years
S.I. = P × R × T/100
Then, (1200 × R × R)/100 = 432
⇒ 12R² = 432
⇒ R² = 36
∴ R = 6%

Ans.6: (d)
Solution: S.I. = Rs. (15500 - 12500) = Rs. 3000.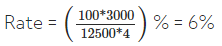


Ans.7: (b)
Solution: Let the sum be Rs. 100. Then,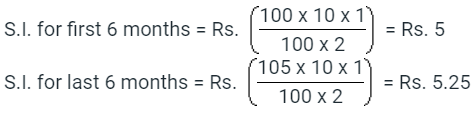

So, amount at the end of 1 year = Rs. (100 + 5 + 5.25) = Rs. 110.25
Effective rate = (110.25 - 100) = 10.25%

Ans.8: (d)
Solution: Given:
B’s Principal = Rs. 5000
C’s Principal = Rs. 3000
Time for B = 2 years
Time for C = 4 years
Formula used:
S.I. = P × R% × T
Where, P = Principal, R = Rate of interest, T = Time
Calculation:
Let the rate of interest for both B and C be R%.
In the case of B:
S.I. = P × R% × T
⇒ S.I. = 5000 × 2 × R/100
⇒ S.I. = 100 × R
In the case of C
S.I. = P × R% × T
⇒ S.I. = 3000 × 4 × R/100
⇒ S.I. = 120 × R
According to the question,
S.I. for B + S.I. for C = 2200
⇒ 100 × R + 120 × R = 2200
⇒ 220 × R = 2200
⇒ R = 10
∴ Rate of interest per annum is 10%.

Ans.9: (e)
Solution: Let the original rate be R%. Then, new rate = (2R)%.
Note: Here, original rate is for 1 year(s); the new rate is for only 4 months i.e. 1/3 year(s).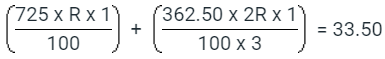

⇒ (2175 + 725) R = 33.50 x 100 x 3
⇒ (2175 + 725) R = 10050
⇒ (2900)R = 10050
⇒ R = 10050/2900 = 3.46
Original rate = 3.46%

Ans.10: (c)
Solution: Given:
The rate of interest is 12%.
Simple interest after 3 years is Rs.5400.
Formula Used:
Simple interest = Principal × Rate × Time/100
Calculation:
Let the principal amount be x.
⇒ SI = x × 12 × 3/100
⇒ 5400 = x × 12 × 3/100
⇒ x = Rs.15000
∴ The principal amount borrowed by him was Rs.15000.

Ans.11: (c)
Solution: SI for 3 years = 12005 - 9800 = Rs. 2205
⇒ SI for 1 years = 2205/3 = Rs. 735
SI for 5 years = 5 × 735 = Rs. 3675
⇒ Principal = 9800 - 3675 = Rs. 6125
As we know, SI = Prt/100
⇒ 3675 = (6125 × r × 5)/100
⇒ r = (3675 × 100) / (5 × 6125)
∴ r = 12%

Ans.12: (c)
Solution: Let the principal be P and rate of interest be R%.
Therefore Required ratio

= 2 : 3

Ans.13: (d)
Solution: Since the principal amount nor original interest rate is not mentioned it is not possible to determine the interest generated.

Ans.14: (a)
Solution: Short trick: 
Difference of rate for 1 years = 6.25% - 4% = 2.25%
The gain in the transaction for 1 years = 5000 × 2.25/100 = 112.5
Detailed Solution
P = Rs. 5000 and time = 2 years
First rate = 4% and Second rate = 6.25%
As we know,
SI = Prt/100
⇒ [5000 × (6.25 - 4) × 1]/100
⇒ [5000 × 2.25 × 1]/100
⇒ 112.5

Ans.15: (a)
Solution: Given:
P = 5000
R = x
T = 3 years
SI = 300 = 5000x × 3/100
Then R = x = (300 × 100/ 3)/ 5000 = 2%

Ans.16: (b)
Solution: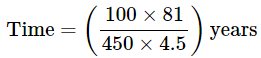 

= 4 years

Ans.17: (d)
Solution: Given: 
B’s Principal = Rs. 5000
C’s Principal = Rs. 3000
Time for B = 2 years
Time for C = 4 years
Formula used: 
S.I. = P × R% × T
Where, P = Principal, R = Rate of interest, T = Time
Calculation: 
Let the rate of interest for both B and C be R%.
In the case of B: 
S.I. = P × R% × T
⇒ S.I. = 5000 × 2 × R/100
⇒ S.I. = 100 × R
In the case of C: 
S.I. = P × R% × T
⇒ S.I. = 3000 × 4 × R/100
⇒ S.I. = 120 × R
According to the question, 
S.I. for B + S.I. for C = 2200
⇒ 100 × R + 120 × R = 2200
⇒ 220 × R = 2200 ⇒ R = 10
∴ Rate of interest per annum is 10%.

Ans.18: (c)
Solution: Given: 
First case: 
P = Rs. 5000, R = 4%, T= 2 years
Second case: 
P = Rs 5000, R = 25/4 %, T = 2 years
Formula used: 
S.I = (P × R × T)/100
Where, S.I = Simple interest, R = Rate %, T = Time
Calculation:
Interest paid by Sachin = (5000 × 4 × 2)/100 = Rs. 400
Interest recieved by Sachin = (5000 × 25/4 × 2)/100 = Rs. 225
His gain for two years = Rs.  625 − Rs. 400 = Rs. 225
His gain per two years = Rs. 225/2 = Rs. 112.50
∴ The gain of one year by Sachin is Rs. 112.50

Ans.19: (b)
Solution: As the rate of interest is same as the time for which money is invested
So, Let rate = R% and time = T years
S.I. = P × R × T/100
Then, (1200 × R × R)/100 = 432
⇒ 12R2 = 432
⇒ R2 = 36
∴ R = 6%

Ans.20: (a)
Solution: Principal = Rs. (1230 x 100/5 x 6) = 4100

Questions Related to Compound Interest

Ans.1: (b)
Solution: Total amount = 1600 ( 1 + 5/2 × 100 )² + 1600 ( 1 + 5/2 × 100)
= 1600 ((41/400 × 14/40 + 41/40))
= 1600 × 41/40(41/40 + 1)
= 1600 × 41 × 81/40 × 40
= 3321
CI earned = 3321 - 3200 = 121

Ans.2: (a)
Solution: Let the sum be x.
We know, Amount = Principal (1 + Rate/100)n
Compound interest = Amount - Principal
CI = x (1 + 4/100)² - x
CI = 51x/625
We know, Simple interest = (P × R × T)/100
SI = (x × 4 × 2)/100 = 2x/25
It is given that CI - SI = 1
⇒ 51x/625 - 2x/25 = 1
⇒ (51x - 50x)/625 = 1
⇒ x = Rs. 625
∴ The sum is Rs. 625.

Ans.3: (c)
Solution: Given:
Increase in salary after 6 years = 60%
Formula Used: 
A = P(1 + r/100)t
Simple Interest = (principal × rate × time)/100
Calculation:
Let the salary at 1st year be 100x
Increased in salary = 60% of 100x = 60x
⇒ 60x = (100x × 6 × R)/100
⇒ R = 10%
Compound Interest after 3 years = P(1 + r/100)t - P
⇒ 12000(1 + 10/100)³ - 12000
⇒ 12000 × (11/10)³ - 12000
⇒ 15972 - 12000 = Rs. 3972
∴ The required answer is Rs 3972.

Ans.4: (a)
Solution: As we know that:
The formula for annual compound interest, including principal sum, is:
A = P (1 + r/n) (nt)
Where: A = the future value of the investment/loan, including interest
P = the principal investment amount (the initial deposit or loan amount)
r = the annual interest rate (decimal)
n = the number of times that interest is compounded per year
t = the number of years the money is invested or borrowed for
C.I. when interest compounded yearly = Rs. 5000 × (1 + 4/100) × (1 + (4/2) /100)
= Rs.(5000 × 26/25 × 51/50) = Rs. 5304.
C.I. when interest is compounded half-yearly = Rs. 5000 × (1 + 2/100) 3
= Rs.(5000 × 51/50 × 51/50 × 51/50) = Rs. 5306.04
Difference = Rs.(5306.04 - 5304) = Rs. 2.04

Ans.5: (a)
Solution: It is given that principal = Rs. 30000
Rate = 7%
Let time period = n
Compound Interest = Rs. 4347
Amount = Principal + Compound interest = Rs. 34347
We know, Amount = Principal (1 + Rate/100)ⁿ
⇒ 34347 = 30000 (1 + 7/100)ⁿ
⇒ 11449/10000 = (107/100)ⁿ
⇒ (107/100)² = (107/100)^t
Time period = 2 years

Ans.6: (c)
Solution: Given: 
Principal = Rs. 25000
Rate of interest = 12% p.a.
Time period = 3 years
Formula Used: 
C.I. = P × ((1 + r/100)t - 1)
Calculations: 
Principal = Rs. 25000
Rate of interest = 12% p.a.
Time period = 3 years
C.I. = P × ((1 + r/100)t - 1)
⇒ C.I. = Rs. 25000 × ((1 + 12/100)3 - 1)
⇒ C.I. = Rs. 10123.20
∴ The compound interest is Rs. 10123.20.

Ans.7: (a)
Solution: Principal = Rs. 1200
Amount = Rs. 1348.32
Time period = 2 years
Let the rate of interest = x%
We know, Amount = Principal (1 + Rate/100)ⁿ
⇒ 1348.32 = 1200 (1 + x/100)² 
⇒ (106/100)2 = (1 + x/100)² 
⇒ 106/100 = 1 + x/100
⇒ x = 6%
∴ The rate should be 6%.

Ans.8: (b)
Solution: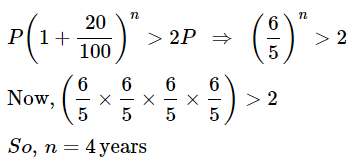 


Ans.9: (c)
Solution: Amount =Rs.[8000 x (1 + 5/100)²]
= Rs.[8000 x 21/20 x 21/20] = Rs.8820.

Ans.10: (d)
Solution: Given: 
Rate = 6%
Formula: 
Amount = P(1 + R/100)n
Calculations: 
Amount of Rs.100 for 1 year when compounded half-yearly
⇒ Rs.[100 × (1 + 3/100)2]
⇒ Rs.106.09
Effective rate = (106.09 − 100)%
⇒ 6.09%
∴ The effective annual rate of interest is 6.09%.

Ans.11: (c)
Solution: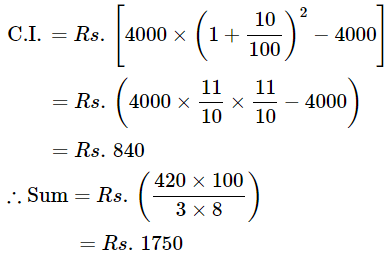 


Ans.12: (a)
Solution: Given: 
S.I on money for 2 year at 5% = Rs. 50
Formula used: 
SI = P * R * T / 100
CA = P(1 + R/n)^nT
where,
P = principal
R = Rate
T = Time
SI = Simple Interest
CA= Compound Interest
Calculation: 
SI = P * R * T/100
50 = P * 5 * 2/100 ; on solving get
P = 500
CA = P(1 + R/n)^nT 
CA = 500 (1 + .05)² then CA with principal = Rs. 551.25
So CA without principal = 551.25 - 500 = Rs. 51.25
Compound Interest = Rs. 51.25

Ans.13: (b)
Solution: 

= Rs.123
∴ Difference = Rs.(123 − 120) = Rs.3

Ans.14: (a)
Solution: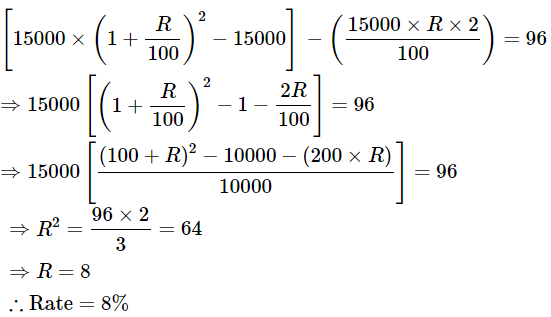 


Ans.15: (b)
Solution: Let the sum be Rs. P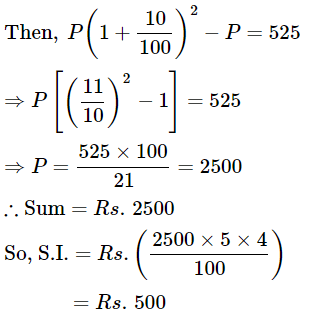


Ans.16: (b)
Solution: Let the sum be Rs.100.
Then, S.I. for first 6 months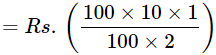

= Rs. 5
S.I. for last 6 months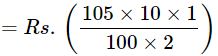

= Rs.5.25 So, amount at the end of 1 year
= Rs. (100 + 5 + 5.25)
= Rs. 110.25
∴ Effective rate = (110.25 - 100) = 10.25%.

Ans.17: (c)
Solution: Since the money becomes Rs. 13380 after 3 years and Rs. 20070 after 6 years
⇒ 20070/13380 = 1.5
That means the money becomes 1.5 times after 3 more years.
∴ Principal = 13380/1.5 = Rs. 8920.

Ans.18: (b)
Solution: As per given question,
Formula: Amount = Principal (1 + Rate/100)^Time 
P(1 + r/100)⁴ = 3P
⇒ (1 + r/100)⁴ = 3
P(1 + r/100)ⁿ = 27P
⇒ (1 + r/100)ⁿ = 27
⇒ (1 + r/100)ⁿ = 33
⇒ (1 + r/100)ⁿ = [(1 + r/100)⁴]³ 
∴ n = 4 × 3 = 12.

Ans.19: (b)
Solution: Here we need to make a comparison on the amount.
Let the principal = P
Rate = 20%
Let time period = n
We know, Amount = Principal (1 + Rate/100)ⁿ
Amount = P (1 + 20/100)ⁿ
We need to know the maximum value of ‘n’ for this amount being more than twice the principal (> 2P)
P (1 + 20/100)ⁿ > 2P
(6/5)ⁿ > 2
If we take n = 1, we get (6/5)¹ = 1.2
If we take n = 2, we get (6/5)² = 1.44
If we take n = 3, we get (6/5)³ = 1.728
If we take n = 4, we get (6/5)⁴ = 2.0736
∴ The time period is 4 years.

Ans.20: (a)
Solution: Let each installment be Rs. x. Then,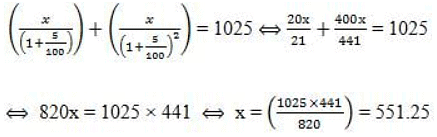

So, value of each installment = Rs. 551.25.