RD Sharma Solutions Ex-24.3, Measures Of Central Tendency, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Find the median of the following data :
Q1 . 83 , 37 , 70 , 29 , 45 , 63 , 41 , 70 , 34 , 54
SOLUTION :
Numbers are 83 , 37 , 70 , 29 , 45 , 63 , 41 , 70 , 34 , 54
Arranging the numbers in ascending order
29 , 34 , 37 , 41 , 45 , 54 , 63 , 70 , 70 , 83
n = 10(even)
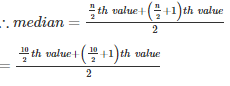
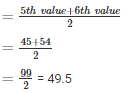
Q2 . 133 , 73 , 89 , 108 , 94 , 104 , 94 , 85 , 100 , 120
SOLUTION :
Numbers are 133 , 73 , 89 , 108 , 94 , 104 , 94 , 85 , 100 , 120
Arranging the numbers in ascending order
73 , 85 , 89 ,94 , 94 , 100 , 104 , 108 , 120 , 133
n = 10(even)
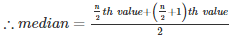
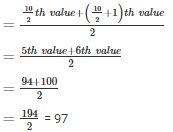
Q3. 31 , 38 , 27 , 28 , 36 , 25 , 35 , 40
SOLUTION :
Numbers are 31 , 38 , 27 , 28 , 36 , 25 , 35 , 40
Arranging the numbers in ascending order
25 , 27 , 28 , 31 , 35 , 36 , 38 , 40
n = 8(even)
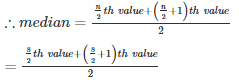
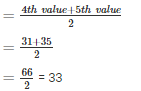
Q4 . 15 , 6 , 16 , 8 , 22 , 21 , 9 , 18 , 25
SOLUTION :
Numbers are 15 , 6 , 16 , 8 , 22 , 21 , 9 , 18 , 25
Arranging the numbers in ascending order
6 , 8 , 9 , 15 , 16 , 21 , 22 , 25
n = 9 (odd)
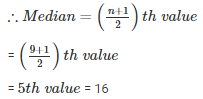
Q5 . 41 , 43 , 127 , 99 , 71 , 92 , 71 , 58 , 57
SOLUTION :
Numbers are 41 , 43 , 127 , 99 , 71 , 92 , 71 , 58 , 57
Arranging the numbers in ascending order
41 , 43 , 57 , 58 , 71 , 71 , 92 , 99 , 127
n = 9 (odd)
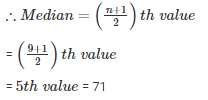
Q6 . 25 , 34 , 31 , 23 , 22 , 26 , 35 , 29 , 20 , 32
SOLUTION :
Numbers are 25 , 34 , 31 , 23 , 22 , 26 , 35 , 29 , 20 , 32
Arranging the numbers in ascending order
20 , 22 , 23 , 25 , 26 , 29 , 31 , 32 , 34 , 35
n = 10(even)
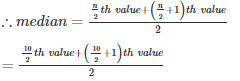
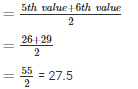
Q7 . 12 , 17 , 3 , 14 , 5 , 8 , 7 , 15
SOLUTION :
Numbers are 12 , 17 , 3 , 14 , 5 , 8 , 7 , 15
Arranging the numbers in ascending order
3 , 5 , 7 , 8 , 12 , 14 , 15 , 17
n = 8(even)
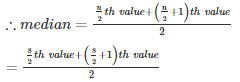
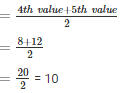
Q8 . 92 , 35 , 67 , 85 , 72 , 81 , 56 , 51 , 42 , 69
SOLUTION :
Numbers are 92 , 35 , 67 , 85 , 72 , 81 , 56 , 51 , 42 , 69
Arranging the numbers in ascending order
35 , 42 , 51 , 56 , 67 , 69 , 72 , 81 , 85 , 92
n = 10(even)
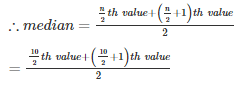
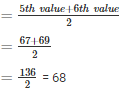
Q9. Numbers 50 , 42 , 35 , 2x + 10 , 2x – 8 , 12 , 11 , 8 are written in descending order and their median is 25 , find x.
SOLUTION :
Given the number of observation , n = 8
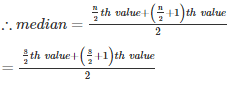

Given median = 25
∴ 2x+1 = 25
⇒ 2x = 24
⇒ x = 12
Q10 . Find the median of the following observations : 46 , 64 , 87 , 41 , 58 , 77 , 35 , 90 , 55 , 92 , 33 .If 92 is replaced by 99 and 41 by 43 in the above data, find the new median?
SOLUTION :
Given the numbers are 46 , 64 , 87 , 41 , 58 , 77 , 35 , 90 , 55 , 92 , 33
Arranging the numbers in ascending order
33 , 35 , 41 , 46 , 55 , 58 , 64 , 77 , 87 , 90 , 92
n = 11 (odd)
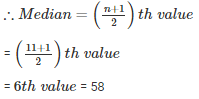
If 92 is replaced by 99 and 41 by 43
Then the new values are : 33 , 35 , 43 , 46 , 55 , 58 , 64 , 77 , 87 , 90 , 99
n = 11 (odd)
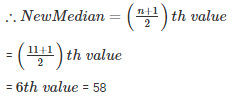
Q11 . Find the median of the following data : 41 , 43 , 127 , 99 , 61 , 92 , 71 , 58 , 57 .If 58 is replaced by 85 , what will be the new median ?
SOLUTION :
Given the numbers are 41 , 43 , 127 , 99 , 61 , 92 , 71 , 58 , 57
Arranging the numbers in ascending order
41 , 43 , 57 , 58 , 61 , 71 , 92 , 99 , 127
n = 9 (odd)
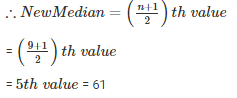
If 58 is replaced by 85
Then the new values be in order are : 41 , 43 , 57, 61 , 71 , 85 , 92 , 99 , 127
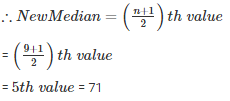
Q12 . The weights (in kg) of 15 students are : 31 , 35 , 27 , 29 , 32 , 43 , 37 , 41 , 34 , 28 , 36 , 44 , 45 , 42 , 30.Find the median . If the weight 44 kg is replaced by 46 kg and 27 kg by 25 kg , find the new median .
SOLUTION :
Given the numbers are 31 , 35 , 27 , 29 , 32 , 43 , 37 , 41 , 34 , 28 , 36 , 44 , 45 , 42 , 30
Arranging the numbers in ascending order
27 , 28 , 29 , 30 , 31 , 32 , 34 , 35 , 36 , 37 , 41 , 42 , 43 , 44 , 45.
n = 15 (odd)
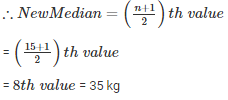
Q13. The following observation s have been arranged in ascending order. If the median of the data is 63 , find the value of x : 29 , 32 , 48 , 50 , x , x + 2 , 72 , 78 , 84 , 95.
SOLUTION :
Total number of observation in the given data is 10 (even number) . So median of this data will be mean of 10/2 i . e, 5th observation and 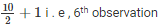
So, median of data 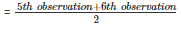
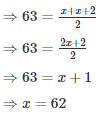
FAQs on RD Sharma Solutions Ex-24.3, Measures Of Central Tendency, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are measures of central tendency in statistics? |  |
| 2. What are the different measures of central tendency? |  |
| 3. How is the mean calculated and what does it represent? |  |
| 4. When is the median a better measure of central tendency than the mean? |  |
| 5. How is the mode useful in data analysis? |  |





















