RD Sharma Solutions for Class 8 Math Chapter 6 - Algebraic Expressions and Identities (Part-4 ) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Multiply:
(5x + 3) by (7x + 2)
Answer 1: To multiply, we will use distributive law as follows:
(5x+3)(7x+2)=5x(7x+2)+3(7x+2)=(5x×7x+5x×2)+(3×7x+3×2)=(35x2+10x)+(21x+6)=35x2+10x+21x+6=35x2+31x+6Thus, the answer is 35x2+31x+635x2+31x+6.
Question 2: Multiply:
(2x + 8) by (x − 3)
Answer 2: To multiply the expressions, we will use the distributive law in the following way:
(2x+8)(x−3)=2x(x−3)+8(x−3)=(2x×x−2x×3)+(8x−8×3)=(2x2−6x)+(8x−24)=2x2−6x+8x−24=2x2+2x−242x+8x-3=2xx-3+8x-3=2x×x-2x×3+8x-8×3=2x2-6x+8x-24=2x2-6x+8x-24=2x2+2x-2Thus, the answer is 2x2+2x−242x2+2x-24.
Question 3: Multiply:
(7x + y) by (x + 5y)
Answer 3: To multiply, we will use distributive law as follows:
(7x+y)(x+5y)=7x(x+5y)+y(x+5y)=7x2+35xy+xy+5y2=7x2+36xy+5y27x+yx+5y=7xx+5y+yx+5y=7x2+35xy+xy+5y2=7x2+36xy+5y2
Thus, the answer is 7x2+36xy+5y27x2+36xy+5y2.
Question 4: Multiply:
(a − 1) by (0.1a2 + 3)
Answer 4: To multiply, we will use distributive law as follows:
(a−1)(0.1a2+3)=0.1a2(a−1)+3(a−1)=0.1a3−0.1a2+3a−3a-10.1a2+3=0.1a2a-1+3a-1=0.1a3-0.1a2+3a-3
Thus, the answer is 0.1a3−0.1a2+3a−30.1a3-0.1a2+3a-3.
Question 5: Multiply:
(3x2 + y2) by (2x2 + 3y2)
Answer 5: To multiply, we will use distributive law as follows:
(3x2+y2)(2x2+3y2)=3x2(2x2+3y2)+y2(2x2+3y2)=6x4+9x2y2+2x2y2+3y4=6x4+11x2y2+3y43x2+y22x2+3y2=3x22x2+3y2+y22x2+3y2=6x4+9x2y2+2x2y2+3y4=6x4+11x2y2+3yThus, the answer is 6x4+11x2y2+3y46x4+11x2y2+3y4.
Question 6: Multiply:
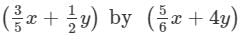
Answer 6: To multiply, we will use distributive law as follows:
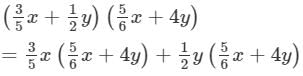
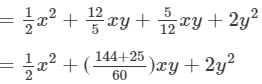
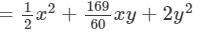
Thus, the answer is 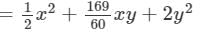
Question 7: Multiply:
(x6 − y6) by (x2 + y2)
Answer 7: To multiply, we will use distributive law as follows:
(x6−y6)(x2+y2)=x6(x2+y2)−y6(x2+y2)=(x8+x6y2)−(y6x2+y8)=x8+x6y2−y6x2−y8 Thus, the answer is x8+x6y2−y6x2−y8x8+x6y2-y6x2-y8.
Question 8: Multiply:
(x2 + y2) by (3a + 2b)
Answer 8: To multiply, we will use distributive law as follows:
(x2+y2)(3a+2b)=x2(3a+2b)+y2(3a+2b)=3ax2+2bx2+3ay2+2by2 Thus, the answer is 3ax2+2bx2+3ay2+2by23ax2+2bx2+3ay2+2by2.
Question 9: Multiply:
[−3d + (−7f)] by (5d + f)
Answer 9: To multiply, we will use distributive law as follows:
[−3d+(−7f)](5d+f)=(−3d)(5d+f)+(−7f)(5d+f)=(−15d2−3df)+(−35df−7f2)=−15d2−3df−35df−7f2=−15d2−38df−7f2Thus, the answer is −15d2−38df−7f2-15d2-38df-7f2.
Question 10: Multiply:
(0.8a − 0.5b) by (1.5a − 3b)
Answer 10: To multiply, we will use distributive law as follows:
(0.8a−0.5b)(1.5a−3b)=0.8a(1.5a−3b)−0.5b(1.5a−3b)=1.2a2−2.4ab−0.75ab+1.5b2=1.2a2−3.15ab+1.5b2Thus, the answer is 1.2a2−3.15ab+1.5b21.2a2-3.15ab+1.5b2.
Question 11: Multiply:
(2x2y2 − 5xy2) by (x2 − y2)
Answer 11: To multiply, we will use distributive law as follows:
(2x2y2−5xy2)(x2−y2)=2x2y2(x2−y2)−5xy2(x2−y2)=2x4y2−2x2y4−5x3y2+5xy4 Thus, the answer is 2x4y2−2x2y4−5x3y2+5xy42x4y2-2x2y4-5x3y2+5xy4.
Question 12: Multiply:
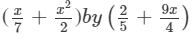
Answer 12: To multiply the expressions, we will use the distributive law in the following way:
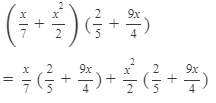
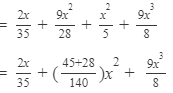
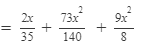
Thus, the answer is 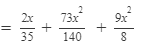
Question 13: Multiply:
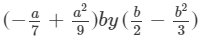
Answer 13: To multiply, we will use distributive law as follows:
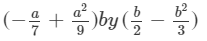
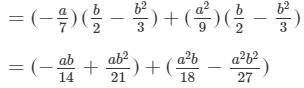
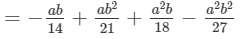
Thus, the answer is 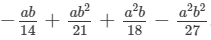
Question 14: Multiply:
(3x2y − 5xy2) by 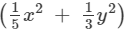
Answer 14: To multiply, we will use distributive law as follows:
(3x2y−5xy2) (1/5 x2+1/3 y2)
= 1/5 x2(3x2y−5xy2)+1/3 y2(3x2y−5xy2)
= 3/5 x4y−x3y2+x2y3−5/3 xy4
Thus, the answer is 3/5 x4y−x3y2+x2y3−5/3 xy4
Question 15: Multiply:
(2x2 − 1) by (4x3 + 5x2)
Answer 15: To multiply, we will use distributive law as follows:
(2x2−1)(4x3+5x2)=2x2(4x3+5x2)−1(4x3+5x2)=8x5+10x4−4x3−5x2Thus, the answer is 8x5+10x4−4x3−5x28x5+10x4-4x3-5x2.
Question 16: (2xy + 3y2) (3y2 − 2)
Answer 16: To multiply, we will use distributive law as follows:
(2xy+3y2)(3y2−2)=2xy(3y2−2)+3y2(3y2−2)=6xy3−4xy+9y4−6y2=9y4+6xy3−6y2−4xyThus, the answer is 9y4+6xy3−6y2−4xy9y4+6xy3-6y2-4xy.
Question 17: Find the following product and verify the result for x = − 1, y = − 2:
(3x − 5y) (x + y)
Answer 17: To multiply, we will use distributive law as follows:
(3x−5y)(x+y)=3x(x+y)−5y(x+y)=3x2+3xy−5xy−5y2=3x2−2xy−5y2∴∴ (3x−5y)(x+y)=3x2−2xy−5y23x-5yx+y=3x2-2xy-5y2.
Now, we put x = −-1 and y = −-2 on both sides to verify the result.
LHS=(3x−5y)(x+y)={3(−1)−5(−2)}{−1+(−2)}=(−3+10)(−3)=(7)(−3)=−21 RHS=3x2−2xy−5y2=3(−1)2−2(−1)(−2)−5(−2)2=3×1−4−5×4=3−4−20=−21 Because LHS is equal to RHS, the result is verified.
Thus, the answer is 3x2−2xy−5y23x2-2xy-5y2.
Question 18: Find the following product and verify the result for x = − 1, y = − 2:
(x2y − 1) (3 − 2x2y)
Answer 18: To multiply, we will use distributive law as follows:
(x2y−1)(3−2x2y)=x2y(3−2x2y)−1×(3−2x2y)=3x2y−2x4y2−3+2x2y=5x2y−2x4y2−3 ∴∴ (x2y−1)(3−2x2y)=5x2y−2x4y2−3x2y-13-2x2y=5x2y-2x4y2-3
Now, we put x = −-1 and y = −-2 on both sides to verify the result.
LHS = (x2y−1)(3−2x2y)=[(−1)2(−2)−1][3−2(−1)2(−2)]=[1×(−2)−1][3−2×1×(−2)]=(−2−1)(3+4)=−3×7=−21RHS=5x2y−2x4y2−3=5(−1)2(−2)−2(−1)4(−2)2−3=[5×1×(−2)]−[2×1×4]−3=−10−8−3=−21 Because LHS is equal to RHS, the result is verified.
Thus, the answer is 5x2y−2x4y2−35x2y-2x4y2-3.
Question 19: Find the following product and verify the result for x = − 1, y = − 2:
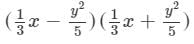
Answer 19: To multiply, we will use distributive law as follows:
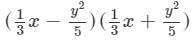
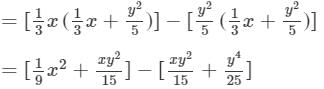
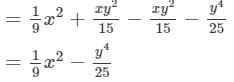
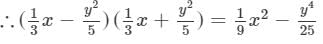
Now, we will put x = −-1 and y = −-2 on both the sides to verify the result.
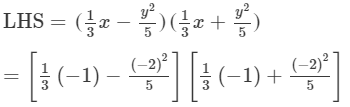
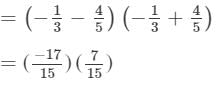
=- 119/225
RHS= 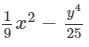
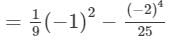
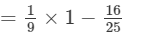
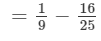
= - 119/225
Because LHS is equal to RHS, the result is verified.
Thus, the answer is 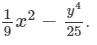
Question 20: Simplify:
x2(x + 2y) (x − 3y)
Answer 20: To simplify, we will proceed as follows:
x2(x+2y)(x−3y)=[x2(x+2y)](x−3y)=(x3+2x2y)(x−3y)=x3(x−3y)+2x2y(x−3y)=x4−3x3y+2x3y−6x2y2=x4−x3y−6x2y2 Thus, the answer is x4−x3y−6x2y2x4-x3y-6x2y2.
Question 21: Simplify:
(x2 − 2y2) (x + 4y) x2y2
Answer 21: To simplify, we will proceed as follows:
(x2−2y2)(x+4y)x2y2=[x2(x+4y)−2y2(x+4y)]x2y2=(x3+4x2y−2xy2−8y3)x2y2=x5y2+4x4y3−2x3y4−8x2y5 Thus, the answer is x5y2+4x4y3−2x3y4−8x2y5x5y2+4x4y3-2x3y4-8x2y5.
Question 22: Simplify:
a2b2(a + 2b)(3a + b)
Answer 22: To simplify, we will proceed as follows:
a2b2(a+2b)(3a+b)=[a2b2(a+2b)](3a+b)=(a3b2+2a2b3)(3a+b)=3a(a3b2+2a2b3)+b(a3b2+2a2b3)=3a4b2+6a3b3+a3b3+2a2b4=3a4b2+7a3b3+2a2b4 Thus, the answer is 3a4b2+7a3b3+2a2b43a4b2+7a3b3+2a2b4.
Question 23: Simplify:
x2(x − y) y2(x + 2y)
Answer 23: To simplify, we will proceed as follows:
x2(x−y)y2(x+2y)=[x2(x−y)][y2(x+2y)]=(x3−x2y)(xy2+2y3)=x3(xy2+2y3)−x2y(xy2+2y3)=x4y2+2x3y3−[x3y3+2x2y4]=x4y2+2x3y3−x3y3−2x2y4=x4y2+x3y3−2x2y4 Thus, the answer is x4y2+x3y3−2x2y4x4y2+x3y3-2x2y4.
Question 24: Simplify:
(x3 − 2x2 + 5x − 7)(2x − 3)
Answer 24: To simplify, we will proceed as follows:
(x3−2x2+5x−7)(2x−3)=2x(x3−2x2+5x−7)−3(x3−2x2+5x−7)=2x4−4x3+10x2−14x−3x3+6x2−15x+21 =2x4−4x3−3x3+10x2+6x2−14x−15x+21=2x4-4x3-3x3+10x2+6x2-14x-15x+21 (Rearranging)
=2x4−7x3+16x2−29x+21=2x4-7x3+16x2-29x+21 (Combining like terms)
Thus, the answer is 2x4−7x3+16x2−29x+212x4-7x3+16x2-29x+21.
Question 25: Simplify:
(5x + 3)(x − 1)(3x − 2)
Answer 25: To simplify, we will proceed as follows:
(5x+3)(x−1)(3x−2)=[(5x+3)(x−1)](3x−2)=[5x(x−1)+3(x−1)](3x−2)=5xx-1+3x-13x-2 (Distributive law)
=[5x2−5x+3x−3](3x−2)=[5x2−2x−3](3x−2)=3x(5x2−2x−3)−2(5x2−2x−3)=15x3−6x2−9x−[10x2−4x−6]=15x3−6x2−9x−10x2+4x+6=5x2-5x+3x-33x-2=5x2-2x-33x-2=3x5x2-2x-3-25x2-2x-3=15x3-6x2-9x-10x2-4x-6=15x3-6x2-9x-10x2+4x+=15x3−6x2−10x2−9x+4x+6=15x3-6x2-10x2-9x+4x+6 (Rearranging)
=15x3−16x2−5x+6=15x3-16x2-5x+6 (Combining like terms)
Thus, the answer is 15x3−16x2−5x+615x3-16x2-5x+6.
Question 26: Simplify:
(5 − x)(6 − 5x)( 2 − x)
Answer 26: To simplify, we will proceed as follows:
(5−x)(6−5x)(2−x)=[(5−x)(6−5x)](2−x) =[5(6−5x)−x(6−5x)](2−x)=56-5x-x6-5x2-x (Distributive law)
=(30−25x−6x+5x2)(2−x)=(30−31x+5x2)(2−x)=2(30−31x+5x2)−x(30−31x+5x2)=60−62x+10x2−30x+31x2−5x3=30-25x-6x+5x22-x=30-31x+5x22-x=230-31x+5x2-x30-31x+5x2=60-62x+10x2-30x+31x2-5x=60−62x−30x+10x2+31x2−5x3=60-62x-30x+10x2+31x2-5x3 (Rearranging)
=60−92x+41x2−5x3=60-92x+41x2-5x3 (Combining like terms)
Thus, the answer is 60−92x+41x2−5x360-92x+41x2-5x3.
Question 27: Simplify:
(2x2 + 3x − 5)(3x2 − 5x + 4)
Answer 27: To simplify, we will proceed as follows:
(2x2+3x−5)(3x2−5x+4)2x2+3x-53x2-5x+4
=2x2(3x2−5x+4)+3x(3x2−5x+4)−5(3x2−5x+4)=2x23x2-5x+4+3x3x2-5x+4-53x2-5x+4 (Distributive law)
=6x4−10x3+8x2+9x3−15x2+12x−15x2+25x−20=6x4-10x3+8x2+9x3-15x2+12x-15x2+25x-20
=6x4−10x3+9x3+8x2−15x2−15x2+12x+25x−20=6x4-10x3+9x3+8x2-15x2-15x2+12x+25x-20 (Rearranging)
=6x4−x3−22x2+36x−20=6x4-x3-22x2+36x-20 (Combining like terms)
Thus, the answer is 6x4−x3−22x2+36x−206x4-x3-22x2+36x-20.
Question 28: Simplify:
(3x − 2)(2x − 3) + (5x − 3)(x + 1)
Answer 28: To simplify, we will proceed as follows:
(3x−2)(2x−3)+(5x−3)(x+1)=[(3x−2)(2x−3)]+[(5x−3)(x+1)] =[3x(2x−3)−2(2x−3)]+[5x(x+1)−3(x+1)]=3x2x-3-22x-3+5xx+1-3x+1 (Distributive law)
=6x2−9x−4x+6+5x2+5x−3x−3=6x2-9x-4x+6+5x2+5x-3x-3
=6x2+5x2−9x−4x+5x−3x−3+6=6x2+5x2-9x-4x+5x-3x-3+6 (Rearranging)
=11x2−11x+3=11x2-11x+3 (Combining like terms)
Thus, the answer is 11x2−11x+311x2-11x+3.
Question 29: Simplify:
(5x − 3)(x + 2) − (2x + 5)(4x − 3)
Answer 29: To simplify, we will proceed as follows:
(5x−3)(x+2)−(2x+5)(4x−3)=[(5x−3)(x+2)]−[(2x+5)(4x−3)] =[5x(x+2)−3(x+2)]−[2x(4x−3)+5(4x−3)]=5xx+2-3x+2-2x4x-3+54x-3 (Distributive law)
=5x2+10x−3x−6−8x2+6x−20x+15=5x2+10x-3x-6-8x2+6x-20x+15
=5x2−8x2+10x−3x+6x−20x−6+15=5x2-8x2+10x-3x+6x-20x-6+15 (Rearranging)
=5x2−8x2+10x−3x+6x−20x−6+15=−3x2−7x+9=5x2-8x2+10x-3x+6x-20x-6+15=-3x2-7x+9(Combining like terms)
Hence, the answer is −3x2−7x+9-3x2-7x+9.
Question 30: Simplify:
(3x + 2y)(4x + 3y) − (2x − y)(7x − 3y)
Answer 30: To simplify, we will proceed as follows:
(3x+2y)(4x+3y)−(2x−y)(7x−3y)=[(3x+2y)(4x+3y)]−[(2x−y)(7x−3y)] =[3x(4x+3y)+2y(4x+3y)]−[2x(7x−3y)−y(7x−3y)]=3x4x+3y+2y4x+3y-2x7x-3y-y7x-3y (Distributive law)
=12x2+9xy+8xy+6y2−[14x2−6xy−7xy+3y2]=12x2+9xy+8xy+6y2−14x2+6xy+7xy−3y2
=12x2−14x2+9xy+8xy+6xy+7xy+6y2−3y2=12x2-14x2+9xy+8xy+6xy+7xy+6y2-3y2 (Rearranging)
=−2x2+30xy+3y2=-2x2+30xy+3y2 (Combining like terms)
Thus, the answer is −2x2+30xy+3y2-2x2+30xy+3y2.
Question 31: Simplify:
(x2 − 3x + 2)(5x − 2) − (3x2 + 4x − 5)(2x − 1)
Answer 31: To simplify, we will proceed as follows:
(x2−3x+2)(5x−2)−(3x2+4x−5)(2x−1)=[(x2−3x+2)(5x−2)]−[(3x2+4x−5)(2x−1)]x2-3x+25x-2-3x2+4x-52x-1=x2-3x+25x-2-3x2+4x-52x-1
=[5x(x2−3x+2)−2(x2−3x+2)]−[2x(3x2+4x−5)−1×(3x2+4x−5)]=5xx2-3x+2-2x2-3x+2-2x3x2+4x-5-1×3x2+4x-5 (Distributive law)
=[5x3−15x2+10x−(2x2−6x+4)]−[6x3+8x2−10x−3x2−4x+5]=[5x3−15x2+10x−2x2+6x−4]−[6x3+8x2−10x−3x2−4x+5]=5x3−15x2+10x−2x2+6x−4−6x3−8x2+10x+3x2+4x−5=5x3-15x2+10x-2x2-6x+4-6x3+8x2-10x-3x2-4x+5=5x3-15x2+10x-2x2+6x-4-6x3+8x2-10x-3x2-4x+5=5x3-15x2+10x-2x2+6x-4-6x3-8x2+10x+3x2+4x-5
=5x3−6x3−15x2−2x2−8x2+3x2+10x+6x+10x+4x−5−4=5x3-6x3-15x2-2x2-8x2+3x2+10x+6x+10x+4x-5-4 (Rearranging)
=−x3−22x2+30x−9 22x2+30x-9 (Combining like terms)
Thus, the answer is −x3−22x2+30x−9-x3-22x2+30x-9.
Question 32: Simplify:
(x3 − 2x2 + 3x − 4) (x −1) − (2x − 3)(x2 − x + 1)
Answer 32: To simplify,we will proceed as follows:
(x3−2x2+3x−4)(x−1)−(2x−3)(x2−x+1)=[(x3−2x2+3x−4)(x−1)]−[(2x−3)(x2−x+1)] =[x(x3−2x2+3x−4)−1(x3−2x2+3x−4)]−[2x(x2−x+1)−3(x2−x+1)]=xx3-2x2+3x-4-1x3-2x2+3x-4-2xx2-x+1-3x2-x+1 (Distributive law)
=[x(x3−2x2+3x−4)−1(x3−2x2+3x−4)]−[2x(x2−x+1)−3(x2−x+1)]=x4−2x3+3x2−4x−x3+2x2−3x+4−[2x3−2x2+2x−3x2+3x−3]=x4−2x3+3x2−4x−x3+2x2−3x+4−2x3+2x2−2x+3x2−3x+3 =x4−2x3−2x3−x3+3x2+2x2+2x2+3x2−4x−3x−2x−3x+4+3=x4-2x3-2x3-x3+3x2+2x2+2x2+3x2-4x-3x-2x-3x+4+3 (Rearranging)
=x4−5x3+10x2−12x+7=x4-5x3+10x2-12x+7 (Combining like terms)
Thus, the answer is x4−5x3+10x2−12x+7x4-5x3+10x2-12x+7.





















