RD Sharma Solutions Ex-8.4, (Part -1), Lines And Angles, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 1: In below fig. AB CD and ∠1and∠2 are in the ratio 3 : 2. Determine all angles from 1 to 8.
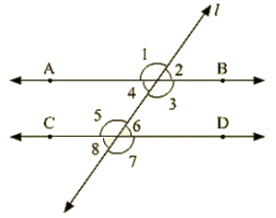
Ans : Let ∠1 = 3x and ∠2 = 2x
∠1 and ∠2 are linear pair of angle
Now, ∠1 and ∠2
⇒ 3x + 2x = 180
⇒ 5x = 180
⇒ x = 180 / 5
⇒ x = 36
∠1 = 3x = 108∘,∠2 = 2x = 72∘
We know, Vertically opposite angles are equal
∠1=∠3 = 108∘
∠2 =∠4 = 72∘
∠6 =∠7=108∘
∠5 =∠8 = 72∘
We also know, corresponding angles are equal
∠1=∠5 = 108∘
∠2 = ∠6 = 72∘
Q 2: In the below fig, I, m and n are parallel lines intersected by transversal p at X. Y and Z respectively. Find ∠1,∠2 and ∠3
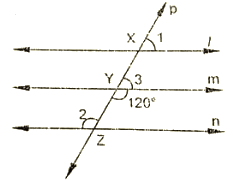
Ans : From the given figure :
∠3+∠mYZ = 180∘ [Linear pair]
⇒ ∠3 =180–120
⇒ ∠3 = 60∘
Now line I parallel to m
∠1 =∠3 [Corresponding angles]
∠1 = 60∘
Also m parallel to n
⇒ ∠2 = 120∘ [Alternative interior angle]
Hence, ∠1 =∠3 = 60∘
∠2 = 120∘
3. In the below fig, AB || CD || EF and GH || KL Find ∠HKL
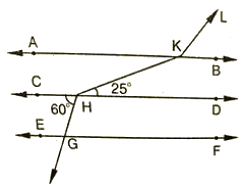
Ans : Produce LK to meet GF at N.
Now, alternative angles are equal
∠CHG = ∠HGN = 60∘
∠HGN = ∠KNF = 60∘ [Corresponding angles]
Hence, ∠KNG = 180–60 = 120
⇒ ∠GNK =∠AKL = 120∘ [Corresponding angles]
∠AKH =∠KHD = 25∘ [alternative angles]
Therefore, ∠HKL=∠AKH+∠AKL = 25+120 = 145∘
Q 4 : In the below fig, show that AB || EF
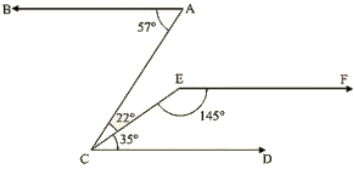
Ans : Produce EF to intersect AC at K.
Now, ∠DCE+∠CEF = 35+145 = 180∘
Therefore, EF || CD (Since Sum of Co-interior angles is 180) —–(1)
Now, ∠BAC =∠ACD = 57∘
⇒ BA || EF [Alternative angles are equal] —–(2)
From (1) and (2)
AB || EF [Since, Lines parallel to the same line are parallel to each other]
Hence proved.
Q 5 : If below fig.if AB || CD and CD || EF, find ∠ACE.
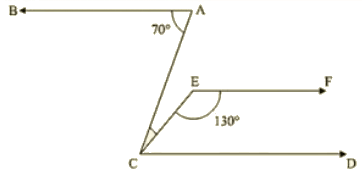
Ans : Since EF || CD
Therefore, EFC + ECD = 180 [co-interior angles are supplementary]
⇒ ECD = 180 – 130 = 50
Also BA || CD
⇒ BAC = ACD = 70 [alternative angles]
But, ACE + ECD =70
⇒ ACE = 70 — 50 = 20
Q 6 : In the below fig, PQ || AB and PR || BC. If ∠QPR = 102∘, determine ∠ABC Give reasons.
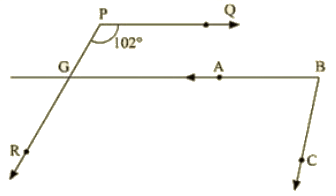
Ans : AB is produce to meet PR at K
Since PQ || AB
∠QPR = ∠BKR = 102∘ [corresponding angles]
Since PR || BC
∠RKB+∠CBK = 180∘ [ Since Corresponding angles are supplementary]
∠CKB=180–102 = 78
∴ ∠CKB = 78°
Q 7 : In the below fig, state Which lines are parallel and why?
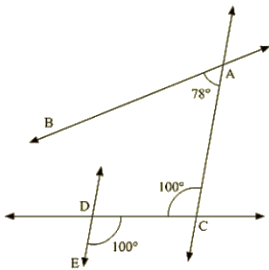
Ans : Vertically opposite angles are equal
⇒ ∠EOC = ∠DOK = 100∘
∠DOK = ∠ACO = 100∘
Here two lines EK and CA cut by a third line and the corresponding angles to it are equal Therefore, EK || AC.
8. In the below fig. if l||m, n || p and ∠1 = 85°. find ∠2.
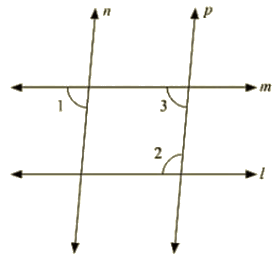
Ans : Corresponding angles are equal
⇒ ∠1=∠3 = 85∘
By using the property of co-interior angles are supplementary
∠2+∠3 = 180∘
∠2+55 = 180
∠2 = 180–85
∠2 = 95∘
Q 9 : If two straight lines are perpendicular to the same line, prove that they are parallel to each other.
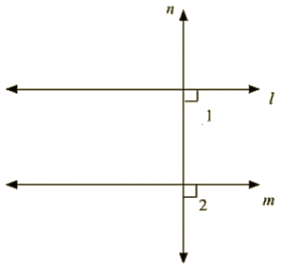
Ans : Given m perpendicular t and l perpendicular to t
∠1=∠2 = 90∘
Since, I and m are two lines and it is transversal and the corresponding angles are equal
L || M
Hence proved
Q 10 : Prove that if the two arms of an angle are perpendicular to the two arms of another angle. then the angles are either equal or supplementary.

Ans : Consider be angles AOB and ACB
Given 0A perpendicular to A0, also 0B perpendicular to BO
To prove : ∠AOB+∠ACB=180∘ (or) ∠AOB+∠ACB = 180∘
Proof : In a quadrilateral = ∠A+∠O+∠B+∠C = 360∘
[ Sum of angles of quadrilateral is 360 ]
⇒ 180+ O +B + C = 360
⇒ O+ C = 360 –180
Hence AOB + ACB = 180 —–(1)
Also, B + ACB = 180
⇒ ACB =180 – 90 = ACES = 90° —–(2)
From (i) and (ii), ACB = A0B = 90
Hence, the angles are equal as well as supplementary.
Q 11 : In the below fig, lines AB and CD are parallel and P is any point as shown in the figure. Show that ∠ABP+∠CDP = ∠DPB.
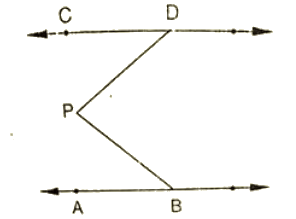
Ans :
Given that AB ||CD
Let EF be the parallel line to AB and CD which passes through P
It can be seen from the figure
Alternative angles are equal
∠ABP = ∠BPF
Alternative angles are equal
∠CDP = ∠DPF
∠ABP+∠CDP = ∠BPF+∠DPF
∠ABP+∠CDP = ∠DPB
Hence proved
AB parallel to CD, P is any point
To prove: ∠ABP+∠BPD+∠CDP = 360∘
Construction : Draw EF || AB passing through P
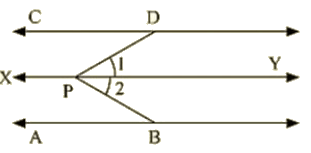
Proof : Since AB ||EF and AB || CD, Therefore EF || CD [Lines parallel to the same line are parallel to each other)
∠ABP+∠EPB = 180∘ [Sum of co-interior angles is180)
∠EPD+∠COP = 180∘ —–(1) [Sum of co-interior angles is180)
∠EPD+∠CDP = 180∘ —–(2)
By adding (1) end (2)
∠ABP+∠EPB+∠EPD+∠CDP = (180+180)∘
∠ABP+∠EPB+∠COP = 360∘
Q 12 : In the below fig, AB || CD and P is any point shown in the figure. Prove that : ∠ABP+∠BPD+∠CDP = 360∘
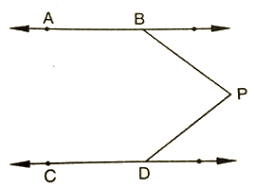
Ans : Through P, draw a line PM parallel to AB or CD.
Now,
A8 || PM ⇒ ABP + BPM = 180
And
CD||PM = MPD + CDP = 180
Adding (i) and (ii), we get A8P + (BPM + MPD) CDP = 360
⇒ ABP + BPD + CDP = 360
Q 13 : Two unequal angles of a parallelogram are in the ratio 2 : 3. Find all its angles in degrees.
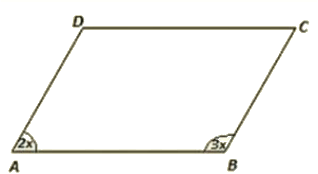
Ans : Let A = 2x and B = 3x
Now, A +B = 180 [Co-interior angles are supplementary]
2x + 3x – 180 [AD II BC and AB is the transversal)
⇒ 5x = 180
x = 180/5
x = 36
Therefore, A = 2 x 36 = 72
b = 3 x 36 = 108
Now, A = C = 72 [Opposite side angles of a parallelogram are equal)
B = D = 108
Q 14 : If each of the two lines is perpendicular to the same line, what kind of lines are they to each other?
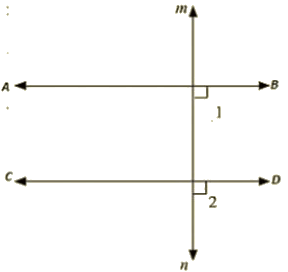
Ans :
Let AB and CD be perpendicular to MN
ABD = 90 [AB perpendicular to MN] —– (i)
CON = 90 [CO perpendicular to MN] —– (ii)
Now, ABD = CDN = 90 (From (i) and (ii))
AB parallel to CD,
Since corresponding angles are equal
FAQs on RD Sharma Solutions Ex-8.4, (Part -1), Lines And Angles, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are the different types of angles in geometry? |  |
| 2. How do you identify corresponding angles? |  |
| 3. What is the sum of interior angles in a triangle? |  |
| 4. How do you find the measure of an angle in a straight line? |  |
| 5. What is the relationship between alternate interior angles? |  |





















