Class 10 Maths Question Answers - Constructions

Q1. Construct a triangle ABC in which BC = 7.5 cm, ∠ B = 45º and the difference between the other two sides is 4 cm.
Steps of construction:
- Take BC = 7.5 cm.
- Construct ∠CBX = 45º.
- From
cut off BD = 4 cm.
- Join D and C.
- Draw the perpendicular bisector of DC which intersects
at A.
- Join A and C.
Thus, ABC is the required triangle.
Q2. Construct a ΔABC whose perimeter is 12 cm and sides are in the ratio 2 : 3 : 4.
Steps of construction:
- Draw
= 12 cm.
- Draw
, making an acute angle with XY in the downward direction.
- From X, set off (2 + 3 + 4 = 9) nine equal distances along XZ.
- Mark points P, Q and R on XZ such that XP = 2 units PQ = 3 units QR = 4 units
- Join RY.
- Draw QC || RY and PB || RY.
- With centre B and radius BX, draw an arc.
- With centre C and radius CY, draw an arc that intersects the previous arc at A.
- Join AB and AC.
Thus, ΔABC is the required triangle.
Q3. Construct ΔABC, in which ∠ B = 60º and ∠ C = 45º and the perpendicular from the vertex A to the base BC is 5.2 cm.
Steps of construction:
- Draw a line PQ.
- Mark a point L on PQ.
- Draw LM ⊥ PQ.
- From
cut off LA = 5.2 cm.
- Draw XY || PQ, through A.
- Construct ∠XAB = 60º and ∠YAC = 45º meeting PQ at B and C respectively.
Thus, ΔABC is the required triangle.
Q4. Construct an equilateral triangle if its altitude is 6 cm. Give justification for your construction.
Steps of construction:
- Draw a line XY and mark a point D on it.
- Construct perpendicular PD on XY.
- Cut off AD = 6 cm
- Make ∠CAD = 30° and ∠BAD = 30° at A on both sides of AD, such that B and C lie on XY.
Thus, ABC is the required triangle.
Justification:
∵ ∠CAD = 30° and ∠ADC = 90°
∴ In ΔADC, ∠C = 180 ∠ (90° + 30°) = 60°
Similarly, ∠B = 60° Also, ∠BAD + ∠CAD = 60°
⇒ ∠A = 60°
Thus, ΔABC is an equilateral triangle in which altitude AD = 6 cm.
Q5. Why we cannot construct a ∆ABC, if ∠A = 60°, AB = 6 cm and AC + BC = 5 cm but construction of ∆ABC is possible if ∠A = 60°, AB = 6 cm and AC – BC = 5 cm?
We know that, by triangle inequality property, construction of triangle is possible if sum of two sides of a triangle is greater than the third side. Here, AC + BC = 5 cm which is less than AB (6 cm) Thus, ∆ABC is not possible.
Also, by triangle inequality property, construction of triangle is possible, if difference of two sides of a triangle is less than the third side
Here, AC – BC = 5 cm, which is less than AB (6 cm)
Thus, ∆ABC is possible.
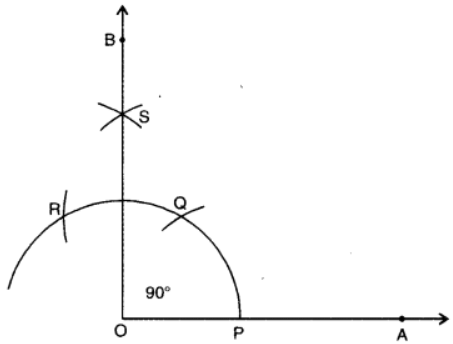
Q6. Construct an angle of 90° at the initial point of the given ray.
Steps of Construction:
- Draw a ray OA.
- With O as centre and any convenient radius, draw an arc, cutting OA at P.
- With P as centre and same radius, draw an arc cutting the arc drawn in step 2 at Q.
- With Q as centre and the same radius as in steps 2 and 3, draw an arc, cutting the arc drawn in step 2 at R.
- With Q and R as centres and same radius, draw two arcs, cutting each other in S.
- Join OS and produce to B.
- Thus, ∠AOB is the required angle of 90°
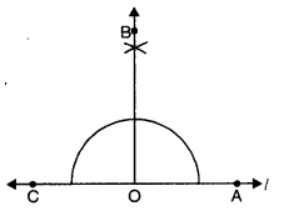
Q7. Draw a straight angle. Using compass bisect it. Name the angles obtained.
Steps of Construction:
- Draw any straight angle (say ∠AOC).
- Bisect ∠AOC and join BO.
- ∠AOB is the required bisector of straight angle AOC.
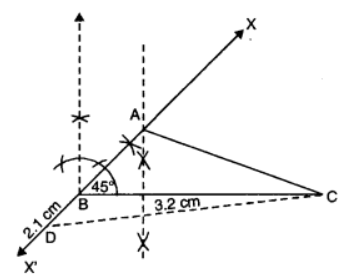
Q8. Construct a ∆ABC such that BC = 3.2 cm, ∠B = 45° and AC – AB = 2.1 cm.
Steps of Construction:
- Draw a line segment BC = 3.2 cm.
- At B, construct an angle ∠CBX = 45° and produce it to point X’.
- Cut-off BD = 2.1 cm and join CD.
- Draw the perpendicular bisector of CD and let it intersect X’BX in A. Join AC.
- Thus, ∆ABC is the required triangle.
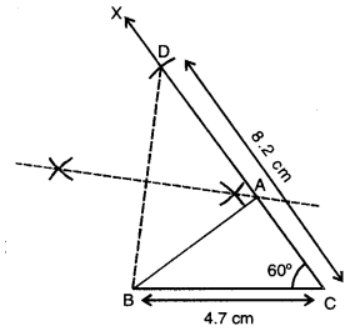
Q9. Construct a triangle ABC in which BC = 4.7 cm, AB + AC = 8.2 cm and ∠C = 60°.
Given: In ∆ABC, BC = 4.7 cm, AB + AC = 8.2 cm and ∠C = 60°.
Required: To construct ∆ABC.
Steps of Construction:
- Draw BC = 4.7 cm.
- Draw From ray CX, cut off CD = 8.2 cm.
- Join BD. Draw the perpendicular bisector of BD meeting CD at A.
- Join AB to obtain the required triangle ABC.
Justification:
∵ A lies on the perpendicular bisector of BD, therefore, AB = AD
Now, CD = 8.2 cm
⇒ AC + AD = 8.2 cm
⇒ AC + AB = 8.2 cm.
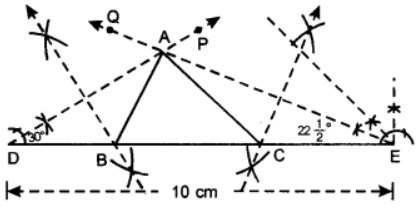
Q10. To construct a triangle, with perimeter 10 cm and base angles 60° and 45°.
Given: In ∆ABC,
AB + BC + CA = 10 cm,
∠B = 60° and ∠C = 45°.
Required: To construct ∆ABC.
Steps of Construction:
- Draw DE = 10 cm.
- At D, construct ∠EDP= 5 of 60°= 30° and at E, construct DEQ = 1 of 45° = 22°
- Let DP and EQ meet at A.
- Draw perpendicular bisector of AD to meet DE at B.
- Draw perpendicular bisector of AE to meet DE at C.
- Join AB and AC.
- Thus, ABC is the required triangle.
|
82 videos|273 docs|69 tests
|
FAQs on Class 10 Maths Question Answers - Constructions
| 1. What are the different types of construction projects? |  |
| 2. What is the role of a construction project manager? |  |
| 3. How is the cost of a construction project estimated? |  |
| 4. What are the steps involved in the construction process? |  |
| 5. How can I ensure the safety of a construction site? |  |