NCERT Solutions for Class 7 Maths - Fractions and Decimals (Exercise 2.1)
| Table of contents |

|
| Exercise 2.1 |

|
| Exercise 2.2 |

|
| Exercise 2.3 |

|
| Exercise 2.4 |

|
| Exercise 2.5 |

|
Exercise 2.1
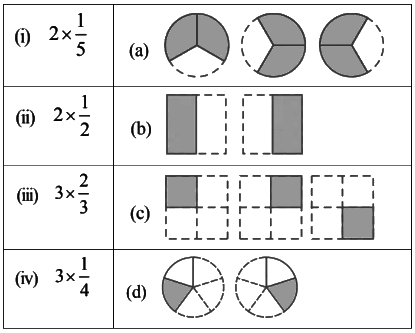
Q1: Which of the drawings (a) to (d) show:
Ans:
(i) 2 × (1/5) represents the addition of 2 figures, each represents 1 shaded part out of the given 5 equal parts.
∴ 2 × (1/5) is represented by fig (d).
(ii) 2 × ½ represents the addition of 2 figures, each represents 1 shaded part out of the given 2 equal parts.
∴ 2 × ½ is represented by fig (b).
(iii) 3 × (2/3) represents the addition of 3 figures, each representing 2 shaded parts out of the given 3 equal parts.
∴ 3 × (2/3) is represented by fig (a).
(iv) 3 × ¼ represents the addition of 3 figures, each represents 1 shaded part out of the given 4 equal parts.
∴ 3 × ¼ is represented by fig (c).
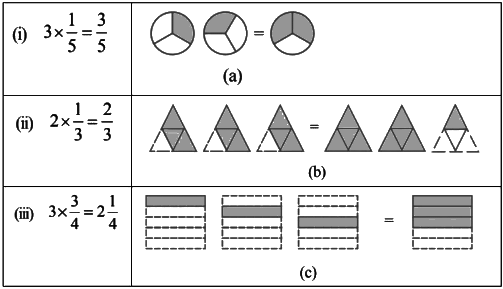
Q2: Some pictures (a) to (c) are given below. Tell which of them show:
Ans:
(i) 3 × (1/5) represents the addition of 3 figures, each represents 1 shaded part out of the given 5 equal parts and (3/5) represents 3 shaded parts out of 5 equal parts.
∴ 3 × (1/5) = (3/5) is represented by fig (c).
(ii) 2 × (1/3) represents the addition of 2 figures, each represents 1 shaded part out of the given 3 equal parts and (2/3) represents 2 shaded parts out of 3 equal parts.
∴ 2 × (1/3) = (2/3) is represented by fig (a).
(iii) 3 × (3/4) represents the addition of 3 figures, each represents 3 shaded part out of the given 4 equal parts and 2 ¼ represents 2 fully and 1 figure having 1 part as shaded out of 4 equal parts.
∴ 3 × (3/4) = 2 ¼ is represented by fig (b)
Q3: Multiply and reduce to lowest form and convert into a mixed fraction:
(i) 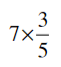
Ans: By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (7/1) × (3/5)
= (7 × 3)/ (1 × 5)
= (21/5)
= 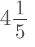
(ii) 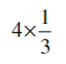
Ans: By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (4/1) × (1/3)
= (4 × 1)/ (1 × 3)
= (4/3)
= 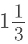
(iii)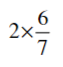
Ans: By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (2/1) × (6/7)
= (2 × 6)/ (1 × 7)
= (12/7)
= 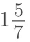
(iv) 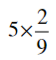
Ans: By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (5/1) × (2/9)
= (5 × 2)/ (1 × 9)
= (10/9)
= 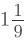
(v) 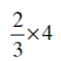
Ans: By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (2/3) × (4/1)
= (2 × 4)/ (3 × 1)
= (8/3)
= 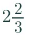
(vi) 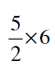
Ans: By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (5/2) × (6/1)
= (5 × 6)/ (2 × 1)
= (30/2)
= 15
(vii) 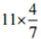
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (11/1) × (4/7)
= (11 × 4)/ (1 × 7)
= (44/7)
= 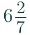
(viii) 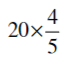
Ans: By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (20/1) × (4/5)
= (20 × 4)/ (1 × 5)
= (80/5)
= 16
(ix) 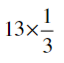
Ans: By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (13/1) × (1/3)
= (13 × 1)/ (1 × 3)
= (13/3)
= 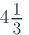
(x) 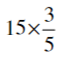
Ans: By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (15/1) × (3/5)
= (15 × 3)/ (1 × 5)
= (45/5)
= 9
Q4: Shade:

Ans: (i) From the question,
We may observe that there are 12 circles in the given box. So, we have to shade ½ of the circles in the box.
∴ 12 × ½ = 12/2
= 6
So we have to shade any 6 circles in the box.
(ii) From the question,
We may observe that there are 9 triangles in the given box. So, we have to shade 2/3 of the triangles in the box.
∴ 9 × (2/3) = 18/3
= 6
So we have to shade any 6 triangles in the box.
(iii) From the question,
We may observe that there are 15 squares in the given box. So, we have to shade 3/5 of the squares in the box.
∴ 15 × (3/5) = 45/5
= 9
So we have to shade any 9 squares in the box.
Q5: Find:
(a) 1/2 of (i) 24 (ii) 46
Ans: (i) 24
We have,
= ½ × 24
= 24/2
= 12
(ii) 46
We have,
= ½ × 46
= 46/2
= 23
(b) 2/3 of (i) 18 (ii) 27
Ans: (i) 18
We have,
= 2/3 × 18
= 2 × 6
= 12
(ii) 27
We have,
= 2/3 × 27
= 2 × 9
= 18
(c) 3/4 of (i) 16 (ii) 36
Ans: (i) 16
We have,
= ¾ × 16
= 3 × 4
= 12
(ii) 36
We have
= ¾ × 36
= 3 × 9
= 27
(d) 4/5 of (i) 20 (ii) 35
Ans: (i) 20
We have,
= 4/5 × 20
= 4 × 4
= 16
(ii) 35
We have,
= 4/5 × 35
= 4 × 7
= 28
Q6: Multiply and express as a mixed fraction:
Ans: First convert the given mixed fraction into improper fraction.
= 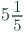 = 26/5
= 26/5
Now,= 3 × (26/5)
= 78/5
= 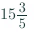
Ans: First convert the given mixed fraction into improper fraction.
= 6 ¾ = 27/4
Now,
= 5 × (27/4)
= 135/4
= 33 ¾
Ans: First convert the given mixed fraction into improper fraction.
= 2 ¼ = 9/4
Now,
= 7 × (9/4)
= 63/4
= 15 ¾
Ans: First convert the given mixed fraction into improper fraction.
= 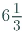 = 19/3
= 19/3
Now,
= 4 × (19/3)
= 76/3
= 
Ans: First convert the given mixed fraction into improper fraction.
= 3 ¼ = 13/4
Now,
= (13/4) × 6
= (13/2) × 3
= 39/2
= 19 ½
Ans: First convert the given mixed fraction into improper fraction.
= 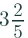 = 17/5
= 17/5
Now,
= (17/5) × 8
= 136/5
= 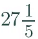
Q7: Find:
Ans: (i) First convert the given mixed fraction into an improper fraction.
= 2 ¾ = 11/4
Now,
= ½ × 11/4
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= ½ × (11/4)
= (1 × 11)/ (2 × 4)
= (11/8)
= 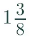
(ii) First convert the given mixed fraction into improper fraction.
= 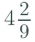 = 38/9
= 38/9
Now,
= ½ × (38/9)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= ½ × (38/9)
= (1 × 38)/ (2 × 9)
= (38/18)
= 19/9
= 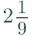
Ans: (i) First convert the given mixed fraction into an improper fraction.
= 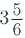 = 23/6
= 23/6
Now,
= (5/8) × (23/6)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (5/8) × (23/6)
= (5 × 23)/ (8 × 6)
= (115/48)
= 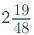
(ii) First convert the given mixed fraction into improper fraction.
= 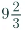 = 29/3
= 29/3
Now,
= (5/8) × (29/3)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
= (5/8) × (29/3)
= (5 × 29)/ (8 × 3)
= (145/24)
= 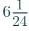
Q8: Vidya and Pratap went for a picnic. Their mother gave them a water bottle that contained 5 litres of water. Vidya consumed 2/5 of the water. Pratap consumed the remaining water.
(i) How much water did Vidya drink?
(ii) What fraction of the total quantity of water did Pratap drink?
Ans: (i) From the question, it is given that,
Amount of water in the water bottle = 5 liters
Amount of water consumed by Vidya = 2/5 of 5 liters
= (2/5) × 5
= 2 liters
So, the total amount of water drank by Vidya is 2 liters
(ii) From the question, it is given that,
Amount of water in the water bottle = 5 liters
Then,
Amount of water consumed by Pratap = (1 – water consumed by Vidya)
= (1 – (2/5))
= (5-2)/5
= 3/5
∴ Total amount of water consumed by Pratap = 3/5 of 5 liters
= (3/5) × 5
= 3 liters
So, the total amount of water drank by Pratap is 3 liters
Exercise 2.2
 Fractions and Decimals
Fractions and Decimals
Q1: Find:
(i) 1/4 of
(a) 1/4
(b) 3/5
(c) 4/3
(ii) 1/7 of
(a) 2/9
(b) 6/5
(c) 3/10
Ans:
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
(i)
(a)
(b)
(c)
(ii)
(a)
(b)
(c)
Q2: Multiply and reduce to lowest form (if possible):
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
Ans:
(i) First, convert the given mixed fraction into an improper fraction.
= = 8/3,
= 8/3,
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(ii) By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(iii) By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(iv) By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(v) By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(vi) By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(vii) By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
 Multiplying FractionQ3: Multiply the following fractions:
Multiplying FractionQ3: Multiply the following fractions:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
Ans:
(i) First convert the given mixed fraction into improper fraction.
= 5 ¼ = 21/4
Now,
= (2/5) × (21/4)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(ii) First, convert the given mixed fraction into an improper fraction.
=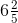 = 32/5Now,= (32/5) × (7/9)
= 32/5Now,= (32/5) × (7/9)
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(iii) First, convert the given mixed fraction into an improper fraction.
=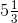 = 16/3
= 16/3
Now,
= (3/2) × (16/3)
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(iv) First convert the given mixed fraction into an improper fraction.
=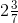 = 17/7
= 17/7
Now,
= (5/6) × (17/7)
By the rule Multiplication of fractions,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(v) First convert the given mixed fraction into improper fraction.
=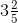 = 17/5
= 17/5
Now,
= (17/5) × (4/7)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(vi) First convert the given mixed fraction into improper fraction.
=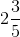 = 13/5
= 13/5
Now,
= (13/5) × (3/1)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
(vii) First convert the given mixed fraction into improper fraction.
=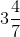 = 25/7
= 25/7
Now,
= (25/7) × (3/5)
By the rule Multiplication of fraction,
Product of fraction = (product of numerator)/ (product of denominator)
Then,
Q4: Which is greater:
(i)
(ii)
Ans:
(i)
⇒
⇒
⇒
(ii)
⇒
⇒
⇒
Q5: Saili plants 4 saplings, in a row, in her garden. The distance between two adjacent saplings is 3/4 m. Find the distance between the first and the last sapling.
Ans: The distance between two adjacent saplings = 3/4 m
Saili planted 4 saplings in a row, then number of gap in saplings = 3
Therefore,
The distance between the first and the last saplings
Thus the distance between the first and the last saplings is
Q6: Lipika reads a book forhours every day. She reads the entire book in 6 days. How many hours in ail were required by her to read the book?
Ans: Time is taken by Lipika to read a book = hours
She reads the entire book in 6 days.
Now, the total hours are taken by her to read the entire book
Thus, 10 hours were required by her to read the book.
Q7: A car runs 16 km using 1 litre of petrol. How much distance will it cover using of petrol?
Ans: In 1 litre of petrol, car covers the distance = 16 km
In litres of petrol, car covers the distance =
Thus, the car will cover 44 km distance.
Q8: (a)
(i) Provide the number in the box
(ii) The simplest form of the number obtained in
(b)
(i) Provide the number in the box
(ii) The simplest form of the number obtained in
Ans:
(a)
(ii) The simplest form
(b)
(ii) The simplest form
Exercise 2.3
Q1:
Find:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Ans:
(i) We have,
= 12 × reciprocal of ¾
(ii) We have,
= 14 × reciprocal of (5/6)
(iii) We have,
= 8× reciprocal of (7/3)
(iv) We have,
= 4 × reciprocal of (8/3)
(v) While dividing a whole number by a mixed fraction, first convert the mixed fraction into improper fraction We have,
=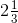 = 7/3
= 7/3
Then,
= 3 ÷ (7/3)
= 3 × reciprocal of (7/3)
(vi) While dividing a whole number by a mixed fraction, first convert the mixed fraction into improper fraction We have,
=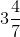 = 25/7
= 25/7
Then,
= 5 ÷ (25/7)
= 5 × reciprocal of (25/7)
Q2: Find the reciprocal of each of the following fractions. Classify the reciprocals as proper fractions, improper fractions and whole numbers.
(i) 3/7
Ans: Reciprocal of (3/7) is (7/3) [∵ ((3/7) × (7/3)) = 1]
So, it is an improper fraction.
Improper fraction is that fraction in which numerator is greater than its denominator.
(ii) 5/8
Ans: Reciprocal of (5/8) is (8/5) [∵ ((5/8) × (8/5)) = 1]
So, it is an improper fraction.
Improper fraction is that fraction in which numerator is greater than its denominator.
(iii) 9/7
Ans: Reciprocal of (9/7) is (7/9) [∵ ((9/7) × (7/9)) = 1]
So, it is a proper fraction.
A proper fraction is that fraction in which denominator is greater than the numerator of the fraction.
(iv) 6/5
Ans: Reciprocal of (6/5) is (5/6) [∵ ((6/5) × (5/6)) = 1]
So, it is a proper fraction.
A proper fraction is that fraction in which denominator is greater than the numerator of the fraction.
(v) 12/7
Ans: Reciprocal of (12/7) is (7/12) [∵ ((12/7) × (7/12)) = 1]
So, it is a proper fraction.
A proper fraction is that fraction in which denominator is greater than the numerator of the fraction.
(vi) 1/8
Ans: Reciprocal of (1/8) is (8/1) or 8 [∵ ((1/8) × (8/1)) = 1]
So, it is a whole number.
Whole numbers are collection of all positive integers including 0.
(vii) 1/11
Ans: Reciprocal of (1/11) is (11/1) or 11 [∵ ((1/11) × (11/1)) = 1]
So, it is a whole number.
Whole numbers are collection of all positive integers including 0.
Q3: Find:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Ans:
(i) We have,
= (7/3) × reciprocal of 2
= (7/3) × (1/2)
(ii) We have,
= (4/9) × reciprocal of 5
= (4/9) × (1/5)
(iii) We have,
= (6/13) × reciprocal of 7
= (6/13) × (1/7)
(iv) First convert the mixed fraction into improper fraction. We have,
=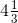 = 13/3 Then,
= 13/3 Then,
= (13/3) × reciprocal of 3
(v) First convert the mixed fraction into improper fraction.
We have,
= 3 ½ = 7/2
Then,
= (7/2) × reciprocal of 4
(vi) First convert the mixed fraction into improper fraction.
We have,
=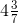 = 31/7
= 31/7
Then,
= (31/7) × reciprocal of 7
Q4: Find
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
(viii)
Ans:
(i) We have,
= (2/5) × reciprocal of ½
= (2/5) × (2/1)
(ii) We have,
= (4/9) × reciprocal of (2/3)
= (4/9) × (3/2)
(iii) We have,
= (3/7) × reciprocal of (8/7)
= (3/7) × (7/8)
(iv) First convert the mixed fraction into improper fraction.
We have,
=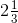 = 7/3
= 7/3
Then,
= (7/3) × reciprocal of (3/5)
(v) First convert the mixed fraction into improper fraction.
We have,
= 3 ½ = 7/2
Then,
= (7/2) × reciprocal of (8/3)
= (7/2) × (3/8)
(vi) First convert the mixed fraction into improper fraction.
We have,
= 1 ½ = 3/2
Then,
= (2/5) × reciprocal of (3/2)
= (2/5) × (2/3)
(vii) First convert the mixed fraction into improper fraction.
We have,
=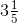 = 16/5
= 16/5
=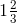 = 5/3Then,= (16/5) × reciprocal of (5/3)= (16/5) × (3/5)
= 5/3Then,= (16/5) × reciprocal of (5/3)= (16/5) × (3/5)
(viii) First convert the mixed fraction into improper fraction.
We have,
=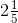 = 11/5
= 11/5
=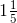 = 6/5
= 6/5
Then,
= (11/5) × reciprocal of (6/5)
= (11/5) × (5/6)
Exercise 2.4

Q1:
Find:
(i) 0.2 x 6
(ii) 8 x 4.6
(iii) 2.71 x 5
(iv) 20.1 x 4
(v) 0.05 x 7
(vi) 211.02 x 4
(vii) 2 x 0.86
Ans:
(i) 0.2 x 6 = 1.2
(ii) 8 x 4.6 = 36.8
(iii) 2.71 x 5 = 13.55
(iv) 20.1 x 4 = 80.4
(v) 0.05 x 7 = 0.35
(vi) 211.02 x 4 = 844.08
(vii) 2 x 0.86 = 1.72
Q2: Find the area of rectangle whose length is 5.7 cm and breadth is 3 cm.
Ans: Given: Length of rectangle = 5.7 cm and
Breadth of rectangle = 3 cm
Area of rectangle = Length x Breadth = 5.7 x 3 = 17.1 cm2
Thus, the area of rectangle is 17.1 cm2.
Q3: Find:
(i) 1.3 x 10
(ii) 36.8 x 10
(iii) 153.7 x 10
(iv) 168.07 x 10
(v) 31.1 x 100
(vi) 156.1 x 100
(vii) 3.62 x 100
(viii) 43.07 x 100
(ix) 0.5 x 10
(x) 0.08 x 10
(xi) 0.9 x 100
(xii) 0.03 x 1000
Ans:
(i) 1.3 x 10 = 13.0
(ii) 36.8 x 10 = 368.0
(iii) 153.7 x 10 = 1537.0
(iv) 168.07 x 10 = 1680.7
(v) 31.1 x 100 = 3110.0
(vi) 156.1 x 100 = 15610.0
(vii) 3.62 x 100 = 362.0
(viii) 43.07 x 100 = 4307.0
(ix) 0.5 x 10 = 5.0
(x) 0.08 x 10 = 0.80
(xi) 0.9 x 100 = 90.0
(xii) 0.03 x 1000 = 30.0
Q4: A two-wheeler covers a distance of 55.3 km in one litre of petrol. How much distance will it cover in 10 litres of petrol?
Ans: ∵ In one litre, a two-wheeler covers a distance = 55.3 km
∴ In 10 litres, a two- wheeler covers a distance = 55.3x10 = 553.0 km
Thus, 553 km distance will be covered by it in 10 litres of petrol.
Q5: Find:
(i) 2.5 x 0.3
(ii) 0.1 x 51.7
(iii) 0.2 x 316.8
(iv) 1.3 x 3.1
(v) 0.5 x 0.05
(vi) 11.2 x 0.15
(vii) 1.07 x 0.02
(viii) 10.05 x 1.05
(ix) 101.01 x 0.01
(x) 100.01 x 1.1
Ans:
(i) 2.5 x 0.3 = 0.75
(ii) 0.1 x 51.7 = 5.17
(iii) 0.2 x 316.8 = 63.36
(iv) 1.3 x 3.1=4.03
(v) 0.5 x 0.05 =0.025
(vi) 11.2 x 0.15 = 1.680
(vii) 1.07 x 0.02 = 0.0214
(viii) 10.05 x 1.05 = 10.5525
(ix) 101.01 x 0.01 = 1.0101
(x) 100.01 x1.1=110.11
Exercise 2.5
Q1: Find:
(i) 0.4 ÷ 2
(ii) 0.35 ÷ 5
(iii) 2.48 ÷ 4
(iv) 65.4 ÷ 6
(v) 651.2 ÷ 4
(v) 14.49 ÷ 7
(vii) 3.96 ÷ 4
(viii) 0.80 ÷ 5
Ans:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
(viii)
Q2: Find:
(i) 4.8 ÷ 10
(ii) 52.5 ÷ 10
(iii) 0.7 ÷ 10
(iv) 33.1 ÷ 10
(v) 272.23 ÷ 10
(vi) 0.56 ÷ 10
(vii) 3.97 ÷ 10
Ans:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
Q3: Find:
(i) 2.7 ÷ 100
(ii) 0.3 ÷ 100
(iii) 0.78 ÷ 100
(iv) 432.6 ÷ 100
(v) 23.6 ÷ 100
(vi) 98.53 ÷ 100
Ans:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Q4: Find:
(i) 7.9 ÷ 1000
(ii) 26.3 ÷ 1000
(iii) 38.53 ÷ 1000
(iv) 128.9 ÷ 1000
(v) 0.5 ÷ 1000
Ans:
(i)
(ii)
(iii)
(iv)
(v)
Q5: Find:
(i) 7÷ 3.5
(ii) 36 ÷ 0.2
(iii) 3.25 ÷ 0.5
(iv) 30.94 ÷ 0.7
(v) 0.5 ÷ 0.25
(vi) 7.75 ÷ 0.25
(vii) 76.5 ÷ 0.15
(viii) 37.8 ÷1.4
(ix) 2.73 ÷ 1.3
Ans:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(vii)
(viii)
(ix)
Q6: A vehicle covers a distance of 43.2 km in 2.4 litres of petrol. How much distance will it cover in one litre petrol?
Ans:
∵ In 2.4 litres of petrol, distance covered by the vehicle = 43.2 km
∴ In 1 litre of petrol, distance covered by the vehicle = 43.2 ÷2.4
Thus, it covered 18 km distance in one litre of petrol.
|
77 videos|386 docs|39 tests
|
FAQs on NCERT Solutions for Class 7 Maths - Fractions and Decimals (Exercise 2.1)
| 1. What are fractions and how are they represented? |  |
| 2. How do you convert a fraction to a decimal? |  |
| 3. What is the difference between proper and improper fractions? |  |
| 4. How can you add or subtract fractions? |  |
| 5. What are some real-life applications of fractions and decimals? |  |
















