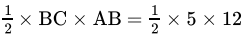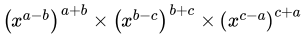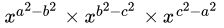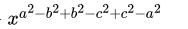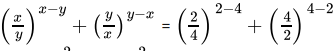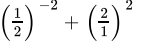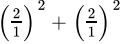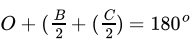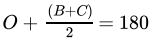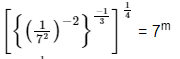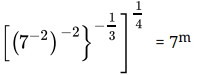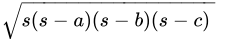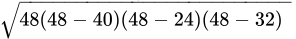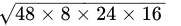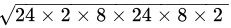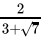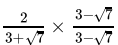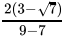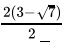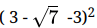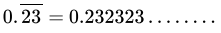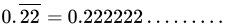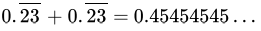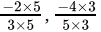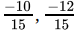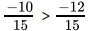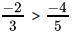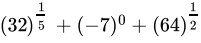Class 9 Math: Sample Question Paper Term I- 6 (With Solutions) | Mathematics (Maths) Class 9 PDF Download
Class 09 Mathematics
Time: 90 Minutes
Max. Marks: 40
General Instructions :
- The question paper contains three parts A, B and C
- Section A consists of 20 questions of 1 mark each. Attempt any 16 questions
- Section B consists of 20 questions of 1 mark each. Attempt any 16 questions.
- Section C consists of 10 questions based on two Case Studies. Attempt any 8 questions.
- There is no negative marking.
Section - A
Q.1: An irrational number between 1/7 and 2/7 is
(a) 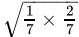
(b) none of these
(c) 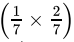
(d) 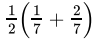
Correct Answer is Option (a)
An irrational number between a and b is given by √ab.
So, an irrational number between 1/7 and 2/7 is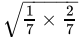
Q.2: Any point on the line y = x is of the form
(a) (a, -a)
(b) (0, a)
(c) (a, 0)
(d) (a, a)
Correct Answer is Option (d)
Every point on the line y = x has same value of x-and y-coordinates i.e., x = a and y = a. Hence, (a, a) is the required form of the solution of the given linear equation.
Q.3: In the given figure, sides CB and BA of ΔBC have been produced to D and E respectively such that ∠ABD = 110° and ∠CAE = 135°. Then ACB =?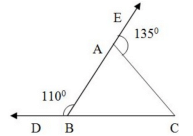
(a) 65°
(b) 35°
(c) 55°
(d) 45°
Correct Answer is Option (a)
∠EAC + ∠BAC = 180° (Linear Pair)∠EAC = 135°
135° + ∠BAC = 180°
∠BAC = 180° - 135°
∠BAC = 45°
∠ABD + ∠ABC = 180° (Linear Pair)
∠ABD = 110°
110° + ∠ABC = 180°
∠ABC = 180° - 110°
∠ABC = 70°
In ΔABC
∠BAC + ∠ABC + ∠ACB = 180°
45° + 70° + ∠ACB = 180°
115° + ∠ACB = 180°
∠ACB = 180° - 115°
∠ACB = 65°
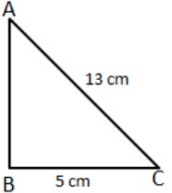
Q.4: The base and hypotenuse of a right triangle are respectively 5 cm and 13 cm long. it is area is:
(a) 30cm2
(b) 28cm2
(c) 25cm2
(d) 40cm2
Correct Answer is Option (a)
AB =
Area =
= 30cm2
Q.5: The value of 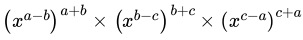 is
is
(a) 3
(b) 2
(c) 1
(d) 0
Correct Answer is Option (c)
⇒
⇒
⇒ x0 = 1
Q.6: The point which lies on y-axis at a distance of 3 units in the negative direction of y-axis is
(a) (0, -3)
(b) (0, 3)
(c) (-3, 0)
(d) (3, 0)
Correct Answer is Option (a)
At the y-axis, the value of x co-ordinate is 0, y-axis at a distance of 3 units in the negative direction, so the co-ordinate of the y-axis is -3.
Q.7: In Fig. if l || m, then x =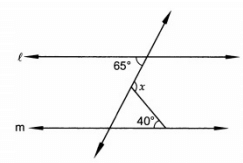
(a) 65°
(b) 25°
(c) 105°
(d) 40°
Correct Answer is Option (c)
Given that,
l ‖ m and n cuts them
Let,
∠1 = 65o
∠2 = x
∠3 = 40o
∠1 = ∠4 = 65o (Alternate angle) (i)
∠3 + ∠4 + ∠5 = 180o (Angle sum property)
40o + 65o + ∠5 = 180o
∠5 = 75o
Now,
∠2 + ∠5 = 180o (Linear pair)
∠x + 75o = 180o
∠x = 105o
Q.8: In figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x, is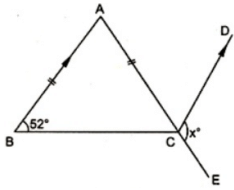
(a) 156°
(b) 76°
(c) 104°
(d) 52°
Correct Answer is Option (c)
B = C (Angles opposite to equal sides are equal)
In ΔABC,
∠A + ∠B+ ∠C= 180°
∠A = 76°
Now,
∠BAC= ∠ACD (Alternate angles)
∠ACD = 76°
Now,
∠ACD + ∠ECD= 180°
∠x = 180 - 76°
∠x = 104°
Q.9: If ‘m’ is a positive integer which is not a perfect square, then √m is
(a) an irrational number
(b) a natural number
(c) an integer
(d) a rational number
Correct Answer is Option (a)
In √m ,if m is not perfect square ,then the value of √m will be m½.
example, √3 ,where 3 is not a perfect square then , √3 = 3½, which is irrationalBut if it is perfect square then value of √m = some integer
Example– √4 =2
Q.10: Given the class intervals 0-10, 10-20, 20-30,…, then 10 is considered in class
(a) 10-30
(b) 0-10
(c) 10-20
(d) 0-20
Correct Answer is Option (c)
As the classes are continuous, the upper limits does not include in that particular class.
Q.11: In the given figure, the measure of √ABC is :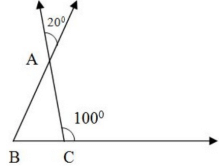
(a) 60°
(b) 80°
(c) 20°
(d) 100°
Correct Answer is Option (b)
∠A = 20° (Verticle Opp Angle)
In ΔABC
the exterior angle so formed is equal to the sum of the two interior opposite angles
∠A +∠ABC = 100°
20° +∠ABC = 100
∠ABC = 100° - 20°
∠ABC = 80°
Q.12: If x = 2 and y = 4, then 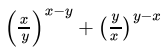 =
=
(a) 8
(b) 2
(c) 12
(d) 4
Correct Answer is Option (a)
Put x = 2 and y = 4,
=
=
= 4 + 4 = 8
Q.13: The sum of two irrational numbers is
(a) always irrational
(b) always rational
(c) always an integer
(d) either irrational or rational
Correct Answer is Option (d)
The sum of two irrational numbers, in some cases, will be irrational. However, if the irrational parts of the numbers have a zero sum (cancel each other out), the sum will be rational.
Q.14: If one of the angles of a triangle is 120°, then the angle between the interior bisectors of the other two angles is
(a) 90°
(b) 60°
(c) 150°
(d) 30°
Correct Answer is Option (c)
Sum of all angles of a triangle is 180o.
If angle A = 120o, then angles B + C = 60
In the triangle formed by the intersection of the bisectors of angles B and C the sum of interior angles is 180o.
Therefore Angles
⇒
⇒ O + 30 = 180⇒ O = 150o
Q.15: Which of the following is not a solution of 2x – 3y = 12?
(a) (0, -4)
(b) (2, 3)
(c) (6, 0)
(d) (3, -2)
Correct Answer is Option (b)
We have to check (2, 3) is a solution of 2x – 3y = 12 if (2, 3) satisfy the equation then (2, 3) solution of 2x – 3y = 12
LHS = 2x - 3y
2 x 2 - 3 x 3
4 - 9 = -5
RHS = -5
LHS ≠ RHS
So (2, 3) is not a solution of 2x - 3y = 12
Q.16: The mean of prime numbers between 30 and 40 is
(a) 37
(b) 36
(c) 34
(d) 31
Correct Answer is Option (c)
Prime numbers between 30 and 40 are 31 and 37.
Mean = 31 + 37/2
Mean = 34
Q.17: If each side of a Δ is halved then its perimeter will be decreased by
(a) 200%
(b) 25%
(c) 70%
(d) 50%
Correct Answer is Option (d)
Perimeter of triangle with sides a, b and c is P = a + b + c. .....(i)
New sides are a/2, b/2, c/2
New perimeter = a + b + c / 2 = P/2 (From eq.(i))Decreased perimeter = P - P/2 = P/2
% of decreased perimeter = (P/2)/P x 100
= 50%
Q.18: A grouped frequency distribution table with classes of equal sizes using 105-120 (120 not included) as one of the class intervals is constructed for the following data: The number of classes in the distribution will be
(a) 7
(b) 4
(c) 5
(d) 6
Correct Answer is Option (d)
Maximum value of the observation is 149 & minimum value is 65.
This range of data need to grouped into classes of equal sizes with 105-120 as one class.
Thus we need to construct classes of width 15.
Below 6 classes can be constructed
60-75, 75-90, 90-105, 105-120, 120-135, 135-150
Q.19: The value of m for which 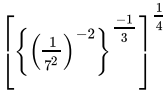 = 7m, is
= 7m, is
(a) -3
(b) 1/4
(c) 2
(d) -1/3
Correct Answer is Option (d)
⇒
⇒
⇒
⇒
⇒Comparing both sides,
m = -1/3
Q.20: In Fig. if lines l and m are parallel, then x =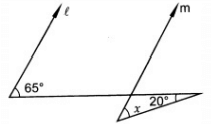
(a) 85°
(b) 20°
(c) 65°
(d) 45°
Correct Answer is Option (d)
l ‖ m
Let transversal be n and 1 = 65o
∠2 = 20o
∠3 = x
Since,
l ‖ m and n cuts them so,
∠1 + ∠4 = 180o (Co. interior angle)
65o + ∠4 = 180o
∠4 = 115o (i)
∠4 = ∠5 = 115o (Vertically opposite angle)
∠2 + ∠5 + ∠3 = 180o
20o+ 115o + ∠x = 180o
∠x = 45o
Section - B
Q.21: The graph of the linear equation 4x + 2y = 12, cuts the x-axis at the point
(a) (3, 0)
(b) (0, -2)
(c) (0, 3)
(d) (-2, 0)
Correct Answer is Option (a)
The graph of the linear equation 4x + 2y = 12, cuts the x-axis at the point
when line cut x axis the co-ordinate of y becomes zero.
so we put y = 0 in given equation to find the co-ordinate
4x + 2y = 12
4x + 2(0) = 12
4x = 12
x = 12/4 = 3
so the required cordinate is (3,0)
Q.22: The lengths of the three sides of a triangular field are 40 m, 24 m and 32 m respectively. The area of the triangle is
(a) 320 m2
(b) 480 m2
(c) 384 m2
(d) 360 m2
Correct Answer is Option (c)
Let:
a = 40 m, b = 24 m and c = 32 m
S = 48 mBy Heron's formula, we have:
Area of triangle =
=
=
=
= 24 x 8 x 2
= 384 m2
Q.23: The area of the triangle formed by the line 2x + 5y = 10 and the co-ordinate axis is
(a) 4 sq. units
(b) 3 sq. units
(c) 5 sq. units
(d) 10 sq. units
Correct Answer is Option (c)
To find the area of the triangle formed by the line 2x + 5y = 10 and co-ordinate axis
We put x = 0 in given equation at x = 0, we get y = 2
at y = 0 we get x = 5
So the line cut y-axis at 2 and x-axis at 5
So the height of the triangle is 2 unit and the base is 5 unit
Area of triangle = 1/2 x base x height
= 1/2 x 2 x 5
= 5 sq. units
Q.24: An exterior angle of a triangle is 80o and two interior opposite angles are equal. Measure of each of these angles is :
(a) 100o
(b) 60o
(c) 120o
(d) 40o
Correct Answer is Option (d)
We know that the exterior angle so formed is equal to the sum of the two interior opposite angles.
Let the two interior opposite angles be x.
So
x + x = 80o
2x = 80o
x = 40o
Q.25: If x = 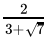 , then (x - 3)2
, then (x - 3)2
(a) 7
(b) 3
(c) 6
(d) 1
Correct Answer is Option (a)
x =
=
=
=
= 3√7
Now (x - 3)2 =
=(-√7)2
= 7
Q.26: The base of a right triangle is 8 cm and hypotenuse is 10 cm. Its area will be :
(a) 48 cm2
(b) 24 cm2
(c) 80 cm2
(d) 40 cm2
Correct Answer is Option (b)
Perpendicular == 6 cm
Area of triangle = 1/2 x Base x Height
= 1/2 x 8 x 6
= 24 sq. cm
Q.27: Tally are usually marked in a bunch of
(a) 5
(b) 4
(c) 3
(d) 6
Correct Answer is Option (a)
Tally are usually marked in a bunch of 5: 4 in a vertical line and one is placed diagonally.
Q.28: The value of 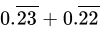 is
is
(a) 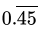
(b) 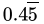
(c) 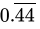
(d) 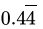
Correct Answer is Option (a)
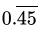
Q.29: The complement of (90 - a)o is
(a) ao
(b) -ao
(c) (90 + 2a)o
(d) (90 - a)o
Correct Answer is Option (a)
We know that the sum of complementary angles are 90o
let the complementary angle of (90 - a)o be x
x + (90 - a)o = 90o
x = 90o- (90 - a)o
x = 90o - 90o ao
x = ao
Q.30: For a given data, the difference between the maximum and minimum observation is known as its
(a) class mark
(b) class
(c) range
(d) class limit
Correct Answer is Option (c)
Difference between maximum and minimum value of observation is called as range.
Q.31: The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude
(a) 24√5cm
(b) 28 cm
(c) 10√5cm
(d) 16√5cm
Correct Answer is Option (a)
24√5cm
Q.32: Select the correct statement from the following
(a) 7/9 > 4/5
(b) -5/7 < -3/4
(c) 2/6 > 3/9
(d) -2/3 > -4/5
Correct Answer is Option (d)
-2/3 > -4/5taking LCM of 3 and 5,
LCM = 15,
So
⇒
now since both the denominator is equal so, we compare its numeratorand since, -10 > -12
So,
thus
Q.33: In the adjoining figure, ∠B = ∠C and AD ⊥ BC. The rule by which ΔABD ≌ ΔADC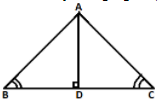
(a) SSS
(b) SAS
(c) RHS
(d) AAS
Correct Answer is Option (d) AAS
As in the given triangles triangle ABD and triangle ACD
AD = AD (common)
Angle ADB = Angle ADC = 90॰ ( As AD perpendicular BC )
Angle B = Angle C ( Given)
Q.34: The mean for counting numbers through 100 is
(a) 55.5
(b) 50.5
(c) 49.5
(d) 51
Correct Answer is Option (b)
Mean of n natural numbers is (n + 1) / 2So,
Mean of 100 numbers = 100 + 1 / 2
Mean of 100 numbers = 101/2 = 50.5
Q.35: In figure, PQ ║ RS, ∠QPR = 70°, ∠ROT = 20° find the value of x.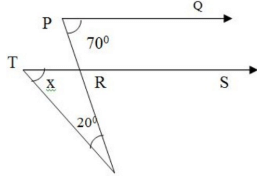
(a) 20°
(b) 70°
(c) 50°
(d) 110°
Correct Answer is Option (c)
PQ ║ RS
∠QPR = ∠SRO = 70° (Corresponding, Angle)
Now in ΔRTO
x + 20° = 70° (exterior angle)
x = 70° - 20°
x = 50°
Q.36: The graphs given in Fig. select the equation whose graph it is from the choices given below: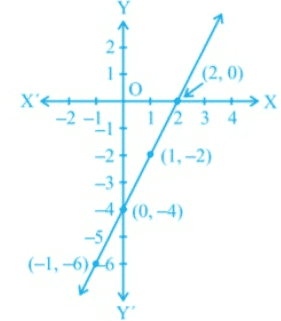
(a) y = 2x
(b) x + y = 0
(c) y = 2x – 4
(d) y = 2x + 1
Correct Answer is Option (d)
The points on the line are (–1, –6), (0, –4), (1, –2), (2, 0). By inspection, you can see that y = 2x – 4 is the equation corresponding to the given graph (line).
Q.37: Side BC of ΔABC has been produced to D on left and to E on right-hand side of BC such that ∠ABD = 125° and ∠ACE = 130°. Then, ∠A = ?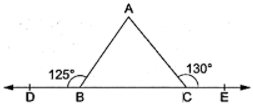
(a) 75°
(b) 50°
(c) 65°
(d) 55°
Correct Answer is Option (a)
We have
∴ ∠ABD + ∠ABC = 180o [ E is a straight line]
⇒ 125o + ∠ABC = 180o
⇒ ∠ABC = 55o
Also,
∠ACE + ∠ACB = 180o
⇒ 130o + ∠ACB = 180o
⇒ ∠ACB = 50o
∴ ∠BAC + ∠ABC + ∠ACB = 180o[Sum of the angles of a triangle]
⇒ ∠BAC + 55o + 50o = 180o
⇒ ∠BAC = 75o
∠A = 75o
Q.38: The value of 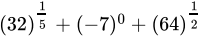 is
is
(a) 10
(b) 0
(c) 11
(d) 1
Correct Answer is Option (c)
= 2 + 1 + 8
= 11
Q.39: To draw a histogram to represent the following frequency distribution :
The adjusted frequency for the class 25-45 is
(a) 6
(b) 5
(c) 2
(d) 3
Correct Answer is Option (c)
Adjusted frequency =
Therefore, Adjusted frequency of 25 - 45 = 8/20 x 5 = 2
Q.40: A grouped frequency table with class intervals of equal size using 3-5 (5 included in this interval) as one of the class intervals is constructed for the following data. The frequency of the class 3-5 is (a) 11(b) 8
(a) 11(b) 8
(c) 5
(d) 3
Correct Answer is Option (a)
count all the numbers in the frequency table between 3 to 5.
Frequency of the numbers from 3 to 5 is 11.
Section - C
Question No. 41 to 45 are based on the given text. Read the text carefully and answer the questions:
Once 4 students from class IX F were selected for plantation of flower plants in the school garden. The selected students were Pankaj, Raju, Deepak and Renu.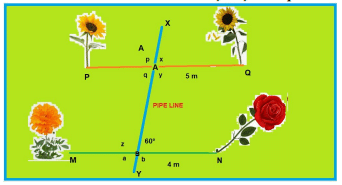
As shown PQ and MN are the parallel lines of the plants.
Pankaj planted a sunflower plant at P, then Raju planted another sunflower at Q.
Further, Deepak was called to plant any flowering plant at point M. He planted a marigold there.
Now it was the turn of Renu, She was told to plant a flowering plant different from the three planted one.
So she planted a rose plat at N.
There was a water pipeline XY which intersects PQ and MN at A and B and ∠XBN = 60°
Q.41: Which angle is the corresponding angle to ∠a?
(a) ∠q
(b) ∠z
(c) ∠b
(d) ∠p
Correct Answer is Option (a)
∠q
Q.42: What is the value of 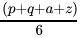 ?
?
(a) 100°
(b) 120°
(c) 60°
(d) 180°
Correct Answer is Option (c)
60°
Q.43: What is the value of ∠z?
(a) 120°
(b) 60°
(c) 100°
(d) 180°
Correct Answer is Option (a)
120°
Q.44: What is the value of ∠x?
(a) 180°
(b) 100°
(c) 120°
(d) 60°
Correct Answer is Option (d)
60°
Q.45: What is the value of p + q?
(a) 100°
(b) 60°
(c) 120°
(d) 180°
Correct Answer is Option (d)
180°
Question No. 46 to 50 are based on the given text. Read the text carefully and answer the questions:
The following data given the weight (in grams) of 30 oranges picked from a basket:
106, 107, 76, 109, 187, 95, 125, 92, 70, 139, 128, 100, 88, 84, 99, 113, 204, 141, 136, 123, 90, 115, 110, 97, 90, 107, 75, 80, 118, 82.
Frequency distribution table: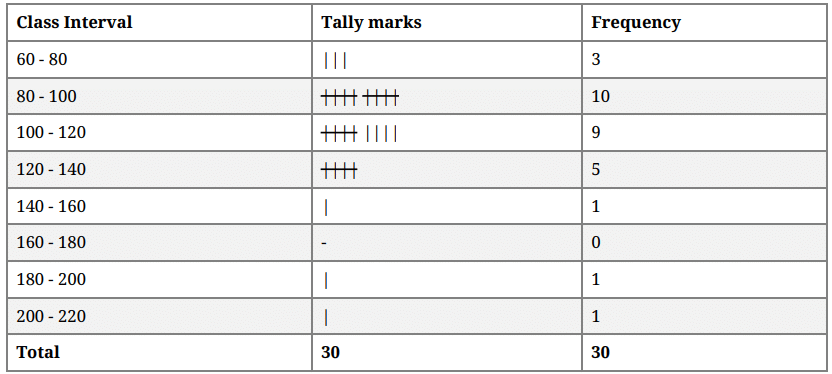

Q.46: Class Size of given class data
(a) 10
(b) 20
(c) 15
(d) 30
Correct Answer is Option (b)
20
Q.47: Classmark of forth class
(a) 20
(b) 130
(c) 70
(d) 15
Correct Answer is Option (b)
130
Q.48: The number of oranges, whose weight is more than 180 g.
(a) 3
(b) 1
(c) 4
(d) 2
Correct Answer is Option (d)
2
Q.49: The number of oranges, whose weight is less than 100 g.
(a) 3
(b) 13
(c) 5
(d) 10
Correct Answer is Option (b)
13
Q.50: The range of data is
(a) 204
(b) 274
(c) 134
(d) 70
Correct Answer is Option (c)
134
|
40 videos|566 docs|57 tests
|