NCERT Solutions for Class 8 Maths - Practical Geometry - 3
Question 1. How will you construct a rectangle PQRS if you know only the lengths PQ and QR?
Solution: A rectangle can be constructed by taking PQ as the length.
Making an ∠90° at Q and cutting off QR, the breadth the ray 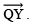 Remaining two points R and S can be located by taking P and R as centres and radii as QR and PQ respectively draw arcs to intersect at S. Thus, PQRS is the required parallelogram.
Remaining two points R and S can be located by taking P and R as centres and radii as QR and PQ respectively draw arcs to intersect at S. Thus, PQRS is the required parallelogram.
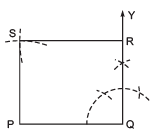
Question 2. Construct the kite EASY if AY = 8 cm, EY = 4 cm and SY = 6 cm. Which properties of the kite did you use in the process?
Solution: Following properties have been used in constructing the KITE:
(i) Diagonals are at right angles.
(ii) One of the diagonal bisects the other.
(iii) Pairs of consecutive sides are equal.
Steps of construction:
I. Draw a line segment AY = 8 cm.
II. Draw , the perpendicular bisector of AY such that it meets AY at O.
III. We cannot locate a point E on PQ at 4 cm from Y and A, i.e. EY = 4 cm = EA is not possible. It is possible only when E and O coincide. In that case the kite does not exist.
EXERCISE 4.5
Question: Draw the following.
1. The square READ with RE = 5.1 cm.
2. A rhombus whose diagonals are 5.2 cm and 6.4 cm long.
3. A rectangle with adjacent sides of lengths 5 cm and 4 cm.
4. A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm.
Solution:1. Steps of construction:
I. Draw a line segment RE = 5.1 cm.
II. At E, draw , such that ∠REX = 90°.
III. From , cut-off
= 5.1 cm.
IV. With centre at A, draw an arc above RE of radius = 5.1 cm.
V. With centre at R, and radius = 5.1 cm, draw another arc to intersect the previous arc at D.
VI. Join DA and DR.
Thus, READ is the required square.
2. Steps of construction:
Note: The diagonals of a rhombus bisect each other at right angles.
I. Draw a line segment AC = 5.2 cm.
II. Draw , the perpendicular bisector of AC.
III. From XY, cut-off OD 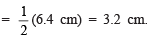
IV. Similarly, cut-off OB 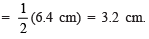
V. Join AD, DC, CB and BA.
Thus, ABCD is the required rhombus.
3. Steps of construction:
I. Draw a line segment PQ = 5 cm.
II. At P, draw , such that ∠QPX = 90°
III. From , cut-off PS = 4 cm.
IV. With centre at 5 and radius = 5 cm, mark an arc towards Q.
V. With centre Q and radius = 4 cm, mark an arc to intersect the previous arc at R.
VI. Join RQ and RS
Thus, PQRS is the required rectangle.
4. Steps of construction:
I. Draw a line segment OK = 5.5 cm.
II. At K, draw a ray .
III. From , cut-off KA = 4.2 cm.
IV. With centre at A and radius = 5.5 cm, draw an arc above OK.
V. With centre O and radius = 4.2 cm, draw another arc to intersect the previous arc at Y.
VI. Join YO and YA.
Thus, OKAY is the required parallelogram.
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Practical Geometry - 3
| 1. What are the different types of triangles based on their sides? |  |
| 2. What are the different types of triangles based on their angles? |  |
| 3. How can we construct an equilateral triangle using a compass and a ruler? |  |
| 4. How can we construct a perpendicular bisector of a line segment? |  |
| 5. How can we construct an angle bisector of an angle? |  |

















