Concept of Supply (Producer Behaviour and Supply) Class 12 Economics
| Table of contents |

|
| Production |

|
| Total Product, Average Product and Marginal Product |

|
| Returns to a Factor |

|
| Shapes of Total Product, Marginal Product and Average Product Curves |

|
| Returns to Scale |

|
| Cost |

|
Production
It is primarily concerned with the transformation of resources into commodities.
Definition of Production Function
- A production function is defined for a given technology.
- It is the technological knowledge that determines the maximum levels of output that can be produced using different combinations of inputs.
- If the technology improves, the maximum levels of output obtainable for different input combinations increase, resulting in a new production function.
Production Function
The inputs that a firm uses in the production process are called factors of production. A firm's production function describes the relationship between output and the factors of production used in the manufacturing process. Our production function tells us the maximum quantity of output (q) that can be produced by using different combinations of these two factors of production – Labour (L) and Capital (K). The production function can be expressed as:
q = f(L, K)
Here, q is equal to the final units of output, L is the amount of labour, and K is the amount of capital. This equation illustrates that different combinations of labour and capital can produce varying levels of output.

Types of Production Functions
There are two types of production functions:
- Short-run Production Function: In this production function, some of the factors of production cannot be varied and remain fixed. This leads to the application of the law of diminishing marginal product. It is also referred to as the variable proportion type of production function.
- Long-run Production Function: In the long run, all production factors are variable. This allows for the application of the law of returns to scale, which includes constant returns to scale (CRS), increasing returns to scale (IRS), and decreasing returns to scale (DRS).

Specific Example of Production Function: A common example of a production function is the Cobb-Douglas production function, which can be expressed as:
q = A * Lα * Kβ
In this function, A represents total factor productivity, while α and β represent the output elasticities of labour and capital, respectively. This function illustrates how output responds to changes in the levels of labour and capital.
Concept of Returns to Scale
- Constant Returns to Scale (CRS): When increasing all inputs by a certain percentage results in an equal percentage increase in output.
- Increasing Returns to Scale (IRS): When increasing all inputs by a certain percentage results in a greater percentage increase in output.
- Decreasing Returns to Scale (DRS): When increasing all inputs by a certain percentage results in a smaller percentage increase in output.
Total Product, Average Product and Marginal Product
Total Product or Total Physical Product
Total product, also known as total return or total physical product of the variable input, represents the total quantity of output produced by a firm using a specific amount of inputs over a certain period. It illustrates the relationship between a variable input and output while keeping all other inputs constant. The total product can be calculated with the formula: Total Product = ∑Qx. This formula shows how variable production factors relate to total output.

Average Product
Average product is the output generated per unit of variable input. It can be calculated using the formula: APL = TP / L.

Marginal Product
The marginal product of an input is defined as the change in output resulting from a one-unit change in the input while keeping all other inputs constant. It reflects the change in total product that occurs with the employment of an additional unit of the variable factor.
Relation between Total, Average and Marginal Product

- When TP rises at an increasing rate, MP rises as well.
- MP decreases as TP increases at a decreasing rate.
- When TP is at its maximum, MP equals zero.
- When TP starts to fall, MP becomes negative.


- When MP is greater than AP, AP increases.
- When MP equals to AP, AP is maximum and constant.
- When MP is less than AP, AP decreases.
- MP can be zero or negative, but AP remains positive.
- AP rises even when MP falls, but MP should be higher than AP.
Returns to a Factor
It describes the output behaviour when only one variable factor of production is increased in the short run while fixed factors remain constant.
Law of Variable Proportion/Law of Diminishing Returns:
This law states that as more units of a variable input (like labor) are applied to a fixed amount of other inputs (like land), the marginal productof the variable input first increases, reaches a maximum, and then begins to decline. This tendency of the marginal product (MP) to first increase and then fall is referred to as the law of variable proportionsor the law of diminishing marginal product.

Why does MP increase initially?
- Initially, as more workers are added to a fixed amount of land, each worker can contribute more effectively, leading to an increase in the marginal product.
Why does MP eventually decrease?
- Once a certain point is reached, adding more workers results in the fixed amount of land becoming insufficient for each worker to operate efficiently. Consequently, the output added by each additional worker becomes proportionally less, leading to a decrease in the marginal product.

- TP Curve: Typically, the Total Product curve will show a rise as more labour is employed, with the rate of increase slowing down as the input continues to increase.
- MP Curve: The Marginal Product curve first rises as additional workers increase total output more efficiently. It reaches a peak (where each worker's contribution is maximized) and then starts to fall as the land becomes overcrowded.
- AP Curve: The Average Product curve generally follows a similar pattern to the MP curve but smoothens out the peaks and troughs seen in the MP curve.
Shapes of Total Product, Marginal Product and Average Product Curves
As one variable input is increased while keeping all other inputs constant, output increases. The shapes of the Total Product (TP), Marginal Product (MP), and Average Product (AP) curves can be described as follows:
- The TP curve shows different output levels obtainable from various units of labour.
- The MP curve is characterized as an inverse 'U'-shaped curve, indicating that the marginal product initially rises and then falls after reaching a certain level of employment.
- The AP curve also follows an inverse 'U'-shaped pattern, rising until the MP falls below it.
Total Product (TP) Curve
The Total Product (TP) curve shows the total output a firm can produce as the amount of one input (labour in this case) is varied while other inputs are kept constant. The TP curve is typically a positively sloped curve that eventually plateaus, reflecting the diminishing returns to the additional input:
- Initial Stage: As labour increases, total output rises rapidly due to better utilization of fixed inputs (like land or machinery).
- Later Stages: As more labour is added, the increase in output becomes less pronounced, reflecting the diminishing marginal product of labour.

Marginal Product (MP) Curve
Marginal Product represents the additional output produced by adding one more unit of input, keeping other inputs constant. The MP curve is described as inverse 'U'-shaped:
- Increasing Phase: Initially, as more workers are employed, each additional worker contributes significantly to output due to factors like increased specialization or efficiencies. This is why MP rises.
- Peak and Decline: The MP reaches a peak when the additional output from one more worker is at its maximum. After this point, as more workers are added, each contributes less to output due to overcrowding or inefficiencies, leading to a fall in MP.
Average Product (AP) Curve
The Average Product is the output per unit of input, calculated by dividing the total output (TP) by the number of units of the input (labor in this case). The AP also typically follows an inverse 'U' shape:
- Initial Correlation with MP: When the first unit of labour is employed, AP and MP are equal because there’s only one unit contributing to output.
- Rise in AP: As labour increases and MP is above AP, the AP continues to rise. This is because the average output per worker is increasing.
- Peak and Decline: AP continues to rise until MP starts to fall below the current AP. At this point, even though more output is being produced, it is at a decreasing rate per worker, causing AP to peak and then decline.
Relationship Between MP and AP
- Intersection at Peak AP: The MP curve intersects the AP curve at the peak of AP. This is because when MP is equal to AP, AP is at its maximum. Before this point, MP is higher than AP, causing AP to rise. After this point, MP is lower than AP, causing AP to decline.

The Law of Variable Proportions
The law of variable proportions states that the marginal product of an input initially increases and subsequently starts to decline after reaching a certain employment level. This behaviour of the marginal product, first rising and then falling, is a key principle in production theory.
Returns to Scale
Returns to scale describe how output changes when all inputs are increased proportionally in the long run.
- Constant Returns to Scale (CRS): If output increases by the same proportion as inputs, productivity per unit of input remains constant.
- Increasing Returns to Scale (IRS): If output increases by a larger proportion than inputs, efficiency improves as production expands.
- Decreasing Returns to Scale (DRS): If output increases by a smaller proportion than inputs, the firm becomes less efficient as it grows.

Cost
Short run Costs
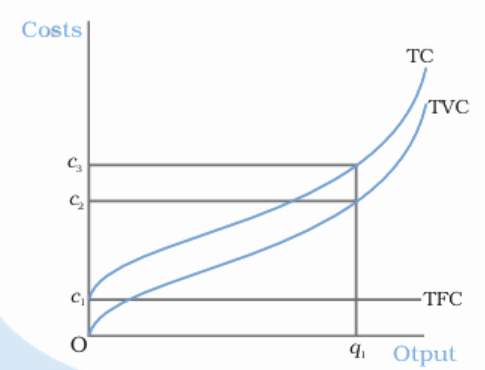
1. Total Cost (TC), Total Fixed Cost (TFC), and Total Variable Cost (TVC)- Total Cost (TC): It is the sum of all costs a firm incurs in the production process and is calculated as the sum of Total Fixed Cost (TFC) and Total Variable Cost (TVC).
- Total Fixed Cost (TFC): These are costs that do not change with the level of output produced, such as rent or salaries of permanent staff.
- Total Variable Cost (TVC): These costs vary directly with the level of production, such as costs for raw materials or hourly wages.

2. Average Costs: SAC, AVC, and AFC
- Short Run Average Cost (SAC): Defined as total cost per unit of output. It includes both variable and fixed costs per unit.

- Average Variable Cost (AVC): This is the variable cost per unit of output.

- Average Fixed Cost (AFC): This is the fixed cost per unit of output, AFC = TFC/q. As output increases, AFC decreases because the fixed cost is spread over more units of output.


3. Marginal Cost (SMC)
- Short Run Marginal Cost (SMC): This measures the additional cost incurred when producing one more unit of output. It is crucial for decision-making regarding production levels.

Shapes of the Short Run Cost Curves
Cost Curves: All these costs can be represented graphically, where output is on the x-axis and cost is on the y-axis.
- TFC Curve: This is a horizontal line since fixed costs do not change with output.
- TVC and TC Curves: These curves slope upwards, reflecting increased costs with higher output levels.

- AVC: AVC starts to fall as output increases due to spreading the variable costs over more units but eventually rises due to diminishing returns. SAC also follows a U-shape, initially decreasing due to spreading out both fixed and variable costs, but later increasing as AVC starts to rise.

- AFC Curve: AFC, or Average Fixed Cost, represents the ratio of Total Fixed Cost (TFC) to the quantity of output (q). Since TFC is constant, as output (q) increases, AFC declines. When output is near zero, AFC becomes extremely large, while as output grows infinitely, AFC approaches zero. The AFC curve takes the shape of a rectangular hyperbola, meaning that for any given output level (q), multiplying q by its corresponding AFC always yields a constant, which is TFC.

- SMC Curve: Also U-shaped, initially falling as efficiencies are gained with small increases in production, then rising as diminishing returns set in.

Behaviour of the Curves
Minimum Points and Intersections:
- The SMC curve intersects both the AVC and SAC curves at their minimum points.
- AVC reaches its minimum before SAC because SAC includes AFC, which continues to decrease even when AVC begins to rise.
- As long as SMC is below AVC or SAC, these average costs decrease. When SMC exceeds AVC or SAC, the average costs start increasing.

Long Run Costs
In the long run, all inputs are variable, which means there are no fixed costs. Therefore, Total Cost (TC) and Total Variable Cost (TVC) are the same. This differs from the short run where some costs remain fixed regardless of the level of output.
Long Run Average Cost (LRAC)
LRAC is the cost per unit of output when all inputs are variable. It is calculated as LRAC=TC/q where q is the quantity of output produced.

Long Run Marginal Cost (LRMC)
LRMC represents the additional cost incurred for producing one more unit of output. This measure helps in deciding how much output to produce to maximize profitability or minimize costs. It can be calculated as:

Returns to Scale and LRAC Curve
The shape of the LRAC curve is significantly influenced by returns to scale:
- Increasing Returns to Scale (IRS): When inputs are increased by a certain proportion and output increases by a larger proportion, it leads to a decrease in average cost as output increases. This causes the downward-sloping portion of the LRAC curve.
- Constant Returns to Scale (CRS): If inputs and output increase by the same proportion, average costs remain constant. This is typically at the minimum point of the LRAC curve.
- Decreasing Returns to Scale (DRS): If a proportional increase in inputs results in a smaller increase in output, average costs rise as output increases. This results in the upward-sloping portion of the LRAC curve.
U-Shaped LRAC Curve
The typical LRAC curve is U-shaped:
- The downward-sloping segment indicates Increasing Returns to Scale (IRS), where average costs decrease as production is scaled up efficiently.
- The minimum point signifies Constant Returns to Scale (CRS), where average costs are minimized, and the firm operates at its highest efficiency.
- The upward-sloping section represents Decreasing Returns to Scale (DRS), showing inefficiencies that arise as the firm becomes excessively large, leading to increased average costs.
Relationship Between LRMC and LRAC
- While LRAC is Falling: LRMC is below LRAC. This is because the marginal cost of producing an additional unit is less than the average cost, thus pulling the average cost down.
- At the Minimum Point of LRAC: LRMC intersects LRAC. This is where average costs are at their lowest and adding one more unit will start increasing average costs.
- While LRAC is Rising: LRMC is above LRAC. Here, the cost of producing one more unit is higher than the average, pushing average costs higher.

|
58 videos|215 docs|44 tests
|
FAQs on Concept of Supply (Producer Behaviour and Supply) Class 12 Economics
| 1. What is the difference between Total Product, Average Product, and Marginal Product? |  |
| 2. What are the stages of Returns to a Factor in production? |  |
| 3. How do the shapes of Total Product, Marginal Product, and Average Product curves differ? |  |
| 4. What is meant by Returns to Scale and how does it differ from Returns to a Factor? |  |
| 5. How do costs relate to production and what are the different types of costs? |  |

|
Explore Courses for Commerce exam
|

|