Open App

Class 7 Exam > Class 7 Notes > Mathematics (Maths) Class 7 > RS Aggarwal Solutions: Decimals (Exercise 3D)

RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7 PDF Download

Q: 5. How can I add and subtract decimal numbers?

Ans. To add or subtract decimal numbers, you can follow these steps:1. Align the decimal points of the numbers.2. Add or subtract the digits in each place value column, starting from the right.3. Carry over any values greater than 9 to the next column.4. If one number has more digits after the decimal point, continue the pattern of zeros and add or subtract as usual.5. Simplify the result, if necessary.For example, to add 3.12 and 1.5, we align the decimal points and add the digits in each place value column: 3 + 1 = 4, 1 + 5 = 6, and 2 + 0 (padding zero) = 2. The sum is 4.62.

Q.1. Divide:
(i) 131.6 by 10
(ii) 32.56 by 10
(iii) 4.38 by 10
(iv) 0.34 by 10
(v) 0.08 by 10
(vi) 0.062 by 10
Ans. We have the following:
(i) 131.6 ÷ 10 = 131.610=13.16131.610=13.16 [Shift the decimal point to the left by 1 place]
(ii) 32.56 ÷ 10 = 32.5610=3.25632.5610=3.256 [Shift the decimal point to the left by 1 place]
(iii) 4.38 ÷ 10 = 4.3810=0.4384.3810=0.438 [Shift the decimal point to the left by 1 place]
(iv) 0.34 ÷ 10 = 0.3410=0.0340.3410=0.034 [Shift the decimal point to the left by 1 place]
(v) 0.08 ÷ 10 = 0.0810=0.0080.0810=0.008 [Shift the decimal point to the left by 1 place]
(vi) 0.062 ÷ 10 = 0.06210=0.00620.06210=0.0062 [Shift the decimal point to the left by 1 place]

Q.2. Divide:
(i) 137.2 by 100
(ii) 23.4 by 100
(iii) 4.7 by 100
(iv) 0.3 by 100
(v) 0.58 by 100
(vi) 0.02 by 100
Ans. We have the following:
(i) 137.2 ÷ 100 = 137.2100=1.372137.2100=1.372 [Shifting the decimal point to the left by 2 places]
(ii) 23.4 ÷ 100 =23.4100=0.23423.4100=0.234 [Shifting the decimal point to the left by 2 places]
(iii) 4.7 ÷ 100 = 4.7100=0.0474.7100=0.047 [Shifting the decimal point to the left by 2 places]
(iv) 0.3 ÷ 100 = 0.3100=0.0030.3100=0.003 [Shifting the decimal point to the left by 2 places]
(v) 0.58 ÷ 100 = 0.58100=0.00580.58100=0.0058 [Shifting the decimal point to the left by 2 places]
(vi) 0.02 ÷ 100 = 0.02100=0.00020.02100=0.0002 [Shifting the decimal point to the left by 2 places]

Q.3. Divide:
(i) 1286.5 by 1000
(ii) 354.16 by 1000
(iii) 38.9 by 1000
(iv) 4.6 by 1000
(v) 0.8 by 1000
(vi) 2 by 1000
Ans. We have the following:
(i) 1286.5 ÷ 1000 = 1286.51000=1.28651286.51000=1.2865 [Shift the decimal point to the left by 3 places]
(ii) 354.16 ÷ 1000 = 354.161000=0.35416354.161000=0.35416 [Shift the decimal point to the left by 3 places]
(iii) 38.9 ÷ 1000 = 38.91000=0.038938.91000=0.0389 [Shift the decimal point to the left by 3 places]
(iv) 4.6 ÷ 1000 = 4.61000=0.00464.61000=0.0046 [Shift the decimal point to the left by 3 places]
(v) 0.8 ÷ 1000 = 0.81000=0.00080.81000=0.0008 [Shift the decimal point to the left by 3 places]
(vi) 2 ÷ 1000 = 21000=0.00221000=0.002 [Shift the decimal point to the left by 3 places]

Q.4. Divide:
(i) 12 by 8
(ii) 63 by 15
(iii) 47 by 20
(iv) 101 by 25
(v) 31 by 40
(vi) 11 by 16
Ans. (i) 12 ÷ 8 = 12/8=3/2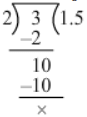
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
∴ 12 ÷ 8 = 1.5
(ii) 63 ÷ 15 = 63/15=21/5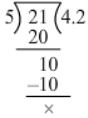

∴ 63 ÷ 15 = 4.2
(iii) 47 ÷ 20 = 47/20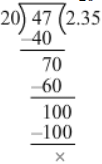

∴ 47 ÷ 20 = 2.35
(iv) 101 ÷ 25 = 101/25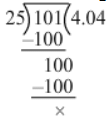

∴ 101 ÷ 25 = 4.04
(v ) 31 ÷ 40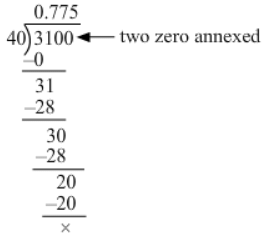

∴ 31 ÷ 40 = 0.775
(vi) 11 ÷ 16 = 11/16

∴ 11 ÷ 16 = 0.6875

Q.5. Divide:
(i) 43.2 by 6
(ii) 60.48 by 12
(iii) 117.6 by 21
(iv) 217.44 by 18
(v) 2.575 by 25
(vi) 6.08 by 8
(vii) 0.765 by 9
(viii) 0.768 by 16
(ix) 0.175 by 25
(x) 0.3322 by 11
(xi) 2.13 by 15
(xii) 6.54 by 12
(xiii) 5.52 by 16
(xiv) 1.001 by 14
(xv) 0.477 by 18
Ans. (i) We have:
43.2 ÷ 6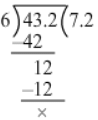
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
∴ 43.2 ÷ 6 = 7.2
(ii) We have:
60.48 ÷ 12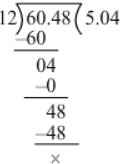

∴ 60.48 ÷ 12 = 5.04
(iii) We have:
117.6 ÷ 21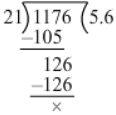

∴ 117.6 ÷ 21 = 5.6
(iv) We have:
217.44 ÷ 18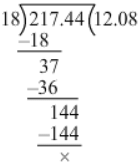

∴ 217.44 ÷ 18 = 12.08
(v) We have:
2.575 ÷ 25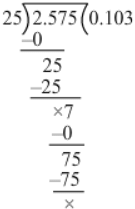

∴ 2.575 ÷ 25 = 0.103
(vi) We have:
6.08 ÷ 8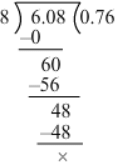
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
∴ 6.08 ÷ 8 = 0.76
(vii) We have:
0.765 ÷ 9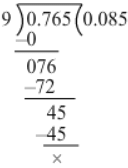

∴ 0.765 ÷ 9 = 0.085
(viii) We have:
0.768 ÷ 16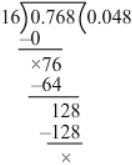

∴ 0.768 ÷ 16 = 0.048
(ix) We have:
0.175 ÷ 25
= 0.175/25
= (0.175×1000) / (25×1000)
= 175 / (25×1000)
= 7/1000
=0.007
(x) We have: 0.3322 ÷ 11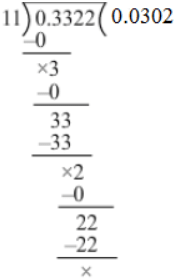
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
∴ 0.3322 ÷ 11 = 0.0302
(xi) We have:
2.13 ÷ 15

∴ 2.13 ÷ 15 = 0.142
(xii) We have:
6.54 ÷ 12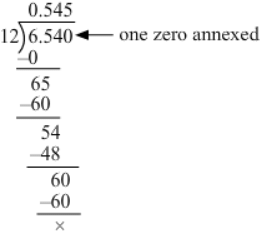

∴ 6.54 ÷ 12 = 0.545
(xiii) We have:
5.52 ÷ 16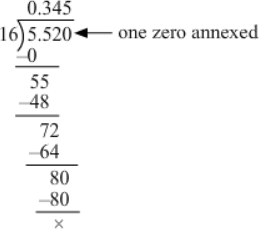

∴ 5.52 ÷ 16 = 0.345
(xiv) We have:
1.001 ÷ 14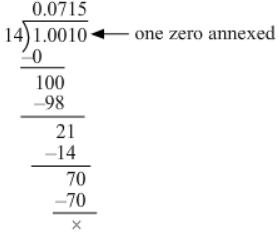

∴ 1.001 ÷ 14 = 0.0715
(xv) We have:
0.477 ÷ 18
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
∴ 0.477 ÷ 18 = 0.0265

Q.6. Divide:
(i) 16.46 ÷ 20
(ii) 403.8 ÷ 30
(iii) 19.2 ÷ 80
(iv) 156.8 ÷ 200
(v) 12.8 ÷ 500
(vi) 18.08 ÷ 400
Ans. (i) 16.46 ÷ 20
= 16.46/20
= (16.46 × 100) / (20×100)
= 1646 / (2×1000)
= 823 / 1000
= 0.823
(ii) 403.8 ÷ 30 = 403.8 / 30
= (403.8×10) / (30×10)
= 4038 / (3×100)
=1346 / 100
=13.46
(iii) 19.2 ÷ 80
= 19.2/80
= 19.2×10/80×10
= 192/800
= 192/8×100
= 24/100
= 0.24
(iv) 156.8 ÷ 200
= 156.8/200
=156.8×10/200×10
=1568/2000
=784/1000
=0.784
(v) 12.8 ÷ 500
= 12.8/500
= (12.8×10) / (500×10)
= 128/5000
= 25.6/1000
= 0.0256
(vi) 18.08 ÷ 400
= 18.08/400
= 18.08×100 / 400×100
= 1808/40000
= 452/10000
=0.0452

Q.7. Divide:
(i) 3.28 by 0.8
(ii) 0.288 by 0.9
(iii) 25.395 by 1.5
(iv) 2.0484 by 0.18
(v) 0.228 by 0.38
(vi) 0.8085 by 0.35
(vii) 21.976 by 1.64
(viii) 11.04 by 1.6
(ix) 6.612 by 11.6
(x) 0.076 by 0.19
(xi) 148 by 0.074
(xii) 16.578 by 5.4
(xiii) 28 by 0.56
(xiv) 204 by 0.17
(xv) 3 by 80
Ans. (i) 3.28 ÷ 0.8
= 3.28/0.8
= (3.28×10) / (0.8×10)
= 32.8/8
Now, we have: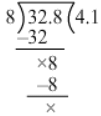
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
∴ 3.280.8=32.88=4.13.280.8=32.88=4.1
(ii) 0.288 ÷ 0.9
= 0.288/0.9
= (0.288×10) / (0.9×10)
= 2.88/9
Now, we have:

∴ 0.2880.9=2.889=0.320.2880.9=2.889=0.32
(iii) 25.395 ÷ 1.5
= 25.395 / 1.5
= (25.395×10) / (1.5×10)
= 253.95/15
Now, we have: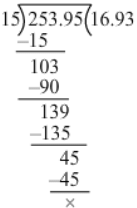
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
∴ 25.395/1.5
= 253.95/15
= 16.93
(iv) 2.0484 ÷ 0.18
= 2.0484/0.18
= (2.0484×100) / (0.18×100)
= 204.84/18
Now, we have: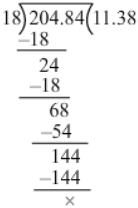

∴ 2.0484/0.18
= 204.84/18
= 11.382.04840.18=204.8418=11.38
(v) 0.228 ÷ 0.38
= 0.228/0.38
= (0.228×100) / (0.38×100)
= 22.8/38
Now, we have: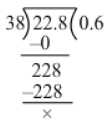
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
∴ 0.2280.38=22.838=0.60.2280.38=22.838=0.6
(vi) 0.8085 ÷ 0.35
= 0.8085/0.35
= (0.8085×100) / (0.35×100)
= 80.85/35
Now, we have: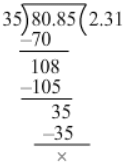

∴0.80850.35=80.8535=2.310.80850.35=80.8535=2.31
(vii) 21.976 ÷ 1.64 = 21.976/1.64
= (21.976×100) / (1.64×100)
= 2197.6/164
Now, we have: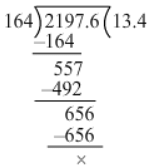
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
∴ 21.9761.64=2197.6164=13.421.9761.64=2197.6164=13.4
(viii) 11.04 ÷ 1.6
= 11.04/1.6
= (11.04×10) / (1.6×10)
= 110.4/16
Now, we have: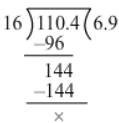

∴11.04/1.6
= 110.4/16
= 6.9
(ix) 6.612 ÷ 11.6
= 6.612/11.6
= (6.612×10) / (11.6×10)
= 66.12/1166
Now, we have: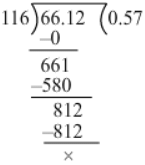
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
∴ 6.612/11.6
= 66.12/116
= 0.57
(x) 0.076 ÷ 0.19
= 0.076/0.19
= (0.076×100) / (0.19×100)
= 7.6/19
Now, we have: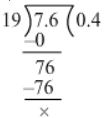

∴ 0.076/0.19
= 7.6/19
= 0.4
(xi) 48 ÷ 0.074
= 148/0.074
= 148×1000/0.074×1000
= 148000/74
= 2×1000
=2000
(xii) 16.578 ÷ 5.4
= 16.578/5.4
= (16.578×10)/(5.4×10)
= 165.78/54
Now, we have: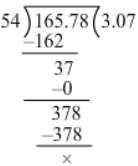
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
∴ 16.578/5.4
= 165.78/54
= 3.07
(xiii) 28 ÷ 0.56
= 28/0.56
= (28×100) / (0.56×100)
= 2800/56
= 1×100/2
= 50
(xiv) 204 ÷ 0.17
= 2040.17
= (204×100) / (0.17×100)
= 20400/17
= 12×100
= 1200
(xv) 3 ÷ 80 = 3/80
Now, we have: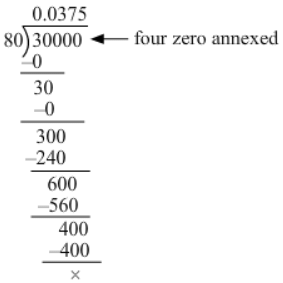
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
∴ 380380 = 0.0375

Q.8. The total cost of 24 chairs is Rs 9255.60. Find the cost of each chair.
Ans. Cost of 24 chairs = Rs 9255.60
∴ Cost of one chair = Rs (9255.60/24)
= Rs (9255.60×10) / (24×10)
= Rs (92556/240)
= Rs 385.65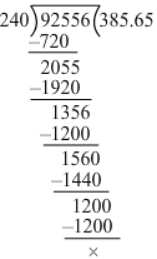
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
Hence, the cost of one chair is Rs 385.65.

Q.9. 1.8 m of cloth is required for a shirt. How many such shirts can be made from a piece of cloth 45 m long?
Ans. Cloth required for 1 shirt = 1.8 m
∴ Number of shirts that can be made from 45 m of cloth
= 45/1.8
=15/0.6
=5/0.2
= 50/2
= 25
Hence, 25 shirts can be made from a piece of cloth of length 45 m.

Q.10. A car covers a distance of 22.8 km in 2.4 litres of petrol. How much distance will it cover in 1 litre of petrol?
Ans. Distance covered by the car with 2.4 litres of petrol = 22.8 km
∴ Distance covered with 1 litre of petrol = (22.8/2.4) km
= (228/24) km
= (228÷12) / (24÷12) km
= (19/2) km
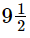= RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7 km
Hence, the distance covered by the car with 1 litre of petrol is 912912 km.

Q.11. A tin holds 16.5 litres of oil. How many such tins will be required to hold 478.5 litres of oil?
Ans. Capacity of 1 tin of oil = 16.5 litres
∴ Number of tins required to hold 478.5 litres of oil = (478.516.5)=(4785165)=(4785÷15165÷15)=31911=29478.516.5=4785165=4785÷15165÷15=31911=29
Hence, 29 oil tins will be required to hold 478.5 litres of oil.

Q.12. The weight of 37 bags of sugar is 3644.5 kg. If all the bags weigh equally, what is the weight of each bag?
Ans. Weight of 37 bags of sugar = 3644.5 kg
∴ Weight of 1 bag of sugar = (3644.5/37)
= 98.5 kg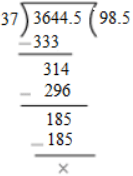
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
Hence, each bag of sugar weighs 98.5 kg.

Q.13. If 69 buckets of equal capacity can be filled with 586.5 litres of water, what is the capacity of eacch bucket?
Ans. Capacity of 69 buckets of water = 586.5 litres
∴ Capacity of one such bucket = (586.5/69) litres = 8.5 litres.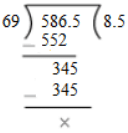
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
Hence, the capacity of each water bucket is 8.5 litres.

Q.14. Monica cuts 46 m of cloth into peices of 1.15 m each. How many pieces does she get?
Ans. Length of one piece of cloth = 1.15 m
∴ Number of pieces she gets from 46 m of cloth = (46/1.15)
= (46×100) / (1.15×100) = (4600/115) = 40
Hence, Monica has 40 pieces of cloth each of length 1.15 m.

Q.15. Mr Soni bought some bags of cement, each weighing 49.8 kg. If the total weight of all the bags is 1792.8 kg, how many bags did he buy?
Ans. Total weight of all the bags of cement = 1792.8 kg
Weight of each bag = 49.8 kg
Number of bags = (Total weight/Weight of each bag)
= (1792.8/49.8)
= (17928/498)
=36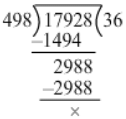
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
Hence, Mr. Soni bought 36 bags of cement.

Q.16. How many pieces of plywood, each 0.35 cm thick, are required to make a pile 1.89 m high?
Ans. Thickness of the pile of plywood pieces = 1.89 m = 189 cm
Thickness of one piece of plywood = 0.35 cm
∴ Required number of plywood pieces = (189/0.35)
=(189×100) / (0.35×100)
= (18900/35)
= 540
RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7
Hence, 540 pieces of plywood are required to make a pile of height 1.89 m.

Q.17. The product of two decimals is 261.36. If one of them is 17.6, find the other.
Ans. Product of the given decimals = 261.36
One decimal = 17.6
The other decimal = 261.36 ÷ 17.6
= (261.36/17.6)
= (261.36×10) / (17.6×10)
=(2613.6/176)
= 14.85
Hence, the other decimal is 14.85.

The document RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7 is a part of the Class 7 Course Mathematics (Maths) Class 7.

All you need of Class 7 at this link: Class 7

	Mathematics (Maths) Class 7 76 videos\|345 docs\|39 tests

Mathematics (Maths) Class 7

76 videos|345 docs|39 tests

Join Course for Free

Top Courses for Class 7

View all

FAQs on RS Aggarwal Solutions: Decimals (Exercise 3D) - Mathematics (Maths) Class 7

1. What are the different types of decimal numbers?

Ans. Decimal numbers can be classified into two types: terminating decimals and non-terminating decimals. Terminating decimals have a finite number of digits after the decimal point, while non-terminating decimals have an infinite number of digits after the decimal point.

2. How can I convert a decimal number into a fraction?

Ans. To convert a decimal number into a fraction, you can follow these steps: 1. Write down the decimal number as the numerator. 2. Determine the denominator by writing 1 followed by the same number of zeros as the number of decimal places in the original number. 3. Simplify the fraction if possible. For example, to convert 0.75 into a fraction, we write 0.75 as the numerator and 100 as the denominator. Simplifying the fraction gives us 3/4.

3. What is the significance of place value in decimal numbers?

Ans. Place value plays a crucial role in decimal numbers. Each digit in a decimal number has a specific place value, which determines its worth. The place values are based on powers of 10. For example, in the number 354.78, the digit 3 is in the hundreds place, the digit 5 is in the tens place, the digit 4 is in the ones place, the digit 7 is in the tenths place, and the digit 8 is in the hundredths place.

4. How can I compare decimal numbers?

Ans. To compare decimal numbers, you can follow these steps: 1. Start by comparing the whole number parts of the decimals. The larger whole number indicates the larger decimal. 2. If the whole number parts are the same, compare the decimal parts from left to right. The first digit that is larger in one decimal determines the larger number. 3. If the decimal parts are the same, but one decimal has additional digits, the decimal with more digits is larger. For example, to compare 2.34 and 2.5, we compare the whole number parts first (both are 2), then compare the tenths place (3 < 5), so 2.5 is larger.

5. How can I add and subtract decimal numbers?

Ans. To add or subtract decimal numbers, you can follow these steps: 1. Align the decimal points of the numbers. 2. Add or subtract the digits in each place value column, starting from the right. 3. Carry over any values greater than 9 to the next column. 4. If one number has more digits after the decimal point, continue the pattern of zeros and add or subtract as usual. 5. Simplify the result, if necessary. For example, to add 3.12 and 1.5, we align the decimal points and add the digits in each place value column: 3 + 1 = 4, 1 + 5 = 6, and 2 + 0 (padding zero) = 2. The sum is 4.62.

Related Exams

Class 7

About this Document

	4.97/5 Rating
	Nov 08, 2024 Last updated

Document Description: RS Aggarwal Solutions: Decimals (Exercise 3D) for Class 7 2024 is part of Mathematics (Maths) Class 7 preparation. The notes and questions for RS Aggarwal Solutions: Decimals (Exercise 3D) have been prepared according to the Class 7 exam syllabus. Information about RS Aggarwal Solutions: Decimals (Exercise 3D) covers topics like and RS Aggarwal Solutions: Decimals (Exercise 3D) Example, for Class 7 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RS Aggarwal Solutions: Decimals (Exercise 3D).

Introduction of RS Aggarwal Solutions: Decimals (Exercise 3D) in English is available as part of our Mathematics (Maths) Class 7 for Class 7 & RS Aggarwal Solutions: Decimals (Exercise 3D) in Hindi for Mathematics (Maths) Class 7 course. Download more important topics related with notes, lectures and mock test series for Class 7 Exam by signing up for free. Class 7: RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7

Description

Full syllabus notes, lecture & questions for RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7 - Class 7 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 7 | Best notes, free PDF download

Information about RS Aggarwal Solutions: Decimals (Exercise 3D)

In this doc you can find the meaning of RS Aggarwal Solutions: Decimals (Exercise 3D) defined & explained in the simplest way possible. Besides explaining types of RS Aggarwal Solutions: Decimals (Exercise 3D) theory, EduRev gives you an ample number of questions to practice RS Aggarwal Solutions: Decimals (Exercise 3D) tests, examples and also practice Class 7 tests

	Mathematics (Maths) Class 7 76 videos\|345 docs\|39 tests

Mathematics (Maths) Class 7

76 videos|345 docs|39 tests

Join Course for Free

Download as PDF

Explore Courses for Class 7 exam

Top Courses for Class 7

Explore Courses

Signup for Free!

Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

Start learning for Free

10M+ students study on EduRev

RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7

past year papers

Semester Notes

Exam

Extra Questions

Objective type Questions

Important questions

RS Aggarwal Solutions: Decimals (Exercise 3D) | Mathematics (Maths) Class 7

Previous Year Questions with Solutions

mock tests for examination

Viva Questions

Free

pdf

Summary

video lectures

shortcuts and tricks

ppt

practice quizzes

study material

MCQs

Sample Paper

;

Additional Information about RS Aggarwal Solutions: Decimals (Exercise 3D) for Class 7 Preparation

RS Aggarwal Solutions: Decimals (Exercise 3D) Free PDF Download

The RS Aggarwal Solutions: Decimals (Exercise 3D) is an invaluable resource that delves deep into the core of the Class 7 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the RS Aggarwal Solutions: Decimals (Exercise 3D) now and kickstart your journey towards success in the Class 7 exam.

Importance of RS Aggarwal Solutions: Decimals (Exercise 3D)

The importance of RS Aggarwal Solutions: Decimals (Exercise 3D) cannot be overstated, especially for Class 7 aspirants. This document holds the key to success in the Class 7 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

RS Aggarwal Solutions: Decimals (Exercise 3D) Notes

RS Aggarwal Solutions: Decimals (Exercise 3D) Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to RS Aggarwal Solutions: Decimals (Exercise 3D). It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, RS Aggarwal Solutions: Decimals (Exercise 3D) Notes on EduRev are your ultimate resource for success.

RS Aggarwal Solutions: Decimals (Exercise 3D) Class 7 Questions

The "RS Aggarwal Solutions: Decimals (Exercise 3D) Class 7 Questions" guide is a valuable resource for all aspiring students preparing for the Class 7 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study RS Aggarwal Solutions: Decimals (Exercise 3D) on the App

Students of Class 7 can study RS Aggarwal Solutions: Decimals (Exercise 3D) alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the RS Aggarwal Solutions: Decimals (Exercise 3D), students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of RS Aggarwal Solutions: Decimals (Exercise 3D) is prepared as per the latest Class 7 syllabus.

Education Revolution

Signup to see your scores go up within 7 days!

Access 1000+ FREE Docs, Videos and Tests

Continue with Google

Takes less than 10 seconds to signup