RD Sharma Solutions Ex-13.2, Linear Equation In Two Variables, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q 1 : Write two solutions for each of the following equations:
(i) 5x – 2y = 7
(ii) x = 6y
(iii) x +πy = 4
(iv) 2/3x – y = 4.
A 1 :
(i) We are given,
3x + 4y = 7
Substituting x = 1
In the given equation,
We get
3 x1 + 4y = 7
4y = 7 – 3 4 = 4Y
Y = I
Thus x = 1 and y = 1 is the solution of 3x + 4y = 7
Substituting x = 2 in the given equation,
we get 3×2 + 4y = 7
4y = 7 – 6
y = 1/4
Thus x = 2 and y = 1/4 is the solution of 3x + 4y = 7
(ii) We are given, x = 6y
Substituting x =0 in the given equation,
we get 0 = 6y
6 y = 0
y = 0
Thus x = 0, ⇒ Solution (0,0)
Substituting x=6
6 = 6y
y = 6/6
y = 1 ⇒ Solution (6,1)
(iii) We are given x+πy = 4
Substituting x = 0 in the given equation,
We get 0+πy = 4
πy = 4
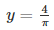
⇒ Solution = 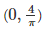
Substituting y = 0 in the given equation, we get
x + 0 = 4
x = 4
⇒ Solution = (4, 0)
(iv) We are given 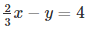
Substituting x = 0 in the given equation, we get
0 – y = 4
y = – 4
Thus x = 0 and y = – 4 is a solution
Substituting x = 3 in the given equation, we get
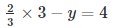
2 – y = 4
y = 2 – 4
y = -2
Thus x = 3 and y = -2 is a solution
Q 2 : Write two solutions of the form x = 0, y = a and x = b, y = 0 for each of the following equations :
(i) 5x – 2y =10
(ii) -4x + 3y =12
(iii) 2x + 3y = 24
A 2 :
(i) We are given,
5x – 2y = 10
Substituting x = 0 in the given equation,
We get;
5×0 – 2y = 10
– 2y = 10
– y = 10/2
y = – 5
Thus x = 0 and y = -5 is the solution of 5x-2y = 10
Substituting y = 0 in the given equation, we get 5x —2 x 0 = 10
5x = 10
x = 10/2
x = 2
Thus x = 2 and y = 0 is a solution of 5x-2y = 10
(ii) We are given, – 4x + 3y = 12
Substituting x = 0 in the given equation,
we get;
-4×0 + 3y = 12
3y = 12
y = 4
Thus x = 0 and y = 4 is a solution of the -4x + 3y = 12
Substituting y = 0 in the given equation, we get;
-4 x + 3 x 0 = 12
– 4x = 12
x =-12/4
x = -3
Thus x = -3 and y =0 is a solution of -4x + 3y = 12
(iii) We are given, 2x + 3y = 24
Substituting x = 0 in the given equation, we get;
2 x 0 + 3y = 24
3y =24
y = 24/3
y = 8
Thus x = 0 and y = 8 is a solution of 2x+ 3y = 24
Substituting y = 0 in the given equation, we get;
2x +3 x 0 = 24
2x = 24
x = 24/2
x =12
Thus x =12 and y = 0 is a solution of 2x + 3y = 24
Q3: Check which of the following are solutions of the equation 2x — y = 6 and Which are not :
(i) (3 , 0)
(ii) (0 , 6)
(iii) (2 , – 2)
(iv) 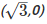
(v)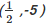
A3:
We are given, 2x – y = 6
(i) In the equation 2 x – y = 6,
We have L.H.S = 2x — y and R.H.S = 6
Substituting x = 3 and y = 0 in 2x – y ,
We get L.H.S = 2 x 3 – 0 = 6
⇒ L.H.S = R.H.S
⇒ (3,0) is a solution of 2x — y = 6.
(ii) In the equation 2x — y = 6,
We have L.H.S = 2x— y and R.H.S = 6
Substituting x = 0 and y = 6 in 2x — y
We get L.H.S = 2 x 0 – 6 = – 6
⇒ L.H.S ≠ R.H.S
⇒ (0,6) is not a solution of 2x — y = 6.
(iii) In the equation 2x — y = 6,
We have L.H.S = 2x – y and R.H.S = 6
Substituting x = 2 and y = – 2 in 2x — y,
We get L.H.S = 2 x 2 – (-2) = 6
⇒ L.H.S = R.H.S
⇒ (2,-2) is a solution of 2x — y = 6.
(iv) In the equation 2x — y = 6,
We have L.H.S = 2x- y and R.H.S=6
Substituting x = √3 and y = 0 in 2x — y,
We get L.H.S = 2 x √3 – 0
⇒ L.H.S ≠ R.H.S
⇒(√3,0)is not a solution of 2x — y = 6.
(v) In the equation 2x — y = 6,
We have L.H.S = 2x – y and R.H.S = 6
Substituting x = 1/2 and y = in 2x — y, we get
L.H.S = 2 x(1/2) – (-5)
⇒1 + 5 = 6
⇒ L.H.S = R.H.S
⇒ 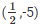 is a solution of 2x — y = 6.
is a solution of 2x — y = 6.
Q4: If x = -1, y = 2 is a solution of the equation 3x + 4y = k, find the value of k.
A4 :
We are given, 3 x + 4 y = k
Given that, (-1,2) is the solution of equation 3x + 4y = k.
Substituting x = -1 and y = 2 in 3x + 4y = k,
We get; 3x – 1 + 4 x 2 = k
K = – 3 + 8
k = 5
Q 5 : Find the value of λ, if x = –λ and y = 5/2 is a solution of the equation x + 4y -7 = 0
A 5 :
We are given,
x + 4y – 7 = 0
(-λ,- 5)is a solution of equation 3x + 4y = k
Substituting x = – λ and y = 5/2 in x + 4y – 7 = 0
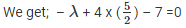
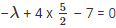
λ = 10 – 7
λ = 3
Q 6 : If x = 2a + 1 and y = a -1 is a solution of the equation 2x – 3y + 5 = 0, find the value of a.
A 6:
We are given, 2x —3y +5 = 0
(2a + 1, a – 1) is the solution of equation 2x – 3y + 5 = 0.
Substituting x = 2a + 1 and y = a – 1 in 2x – 3y + 5 = 0,
We get 2 x 2a + (1- 3) x a – 1 + 5 = 0
⇒ 4a + 2 – 3a + 3 + 5 = 0
⇒ a + 10 = 0
⇒ a = – 10
Q 7 : If x = 1 and y = 6 is a solution of the equation 8x – ay + a2 = 0, find the values of a.
A 7 :
We are given,
8x – ay + a2 = 0
(1 , 6) is a solution of equation 8x — ay + a2 =0
Substituting x = 1 and y = 6 in 8x – ay + a2 = 0 ,we get
8 x 1 – a x 6 + a2 = 0
⇒ a2 – 6a + 8 = 0
Using quadratic factorization
a2 – 4a – 2a + 8 = 0
a(a – 4) – 2 (a – 4) = 0
(a – 2) (a – 4) = 0
a = 2, 4
FAQs on RD Sharma Solutions Ex-13.2, Linear Equation In Two Variables, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are linear equations in two variables? |  |
| 2. How do you solve linear equations in two variables? |  |
| 3. What is the importance of linear equations in two variables? |  |
| 4. Can linear equations in two variables have more than one solution? |  |
| 5. How are linear equations in two variables represented graphically? |  |
















