Types of Forces, Power and Equilibrium | Physics for JEE Main & Advanced PDF Download
Introduction
To grasp the concept of conservative and non-conservative forces, let us examine two scenarios. In the first case, depicted in Figure 1, a mass comes to rest, compressing a spring by a distance 'x'. As the spring returns to its normal length, the mass attains a velocity 'v'. This compression and elongation process repeats, with the maximum compression reaching 'x'. Consequently, we observe that the total mechanical energy of the system (Block + Spring) remains constant.
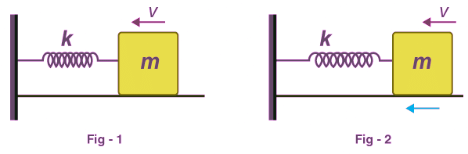
In contrast, the second case also involves compression and elongation, but with a decreasing minimum value. Consequently, the total mechanical energy of the system is not conserved in this scenario. Based on these observations, we can define conservative and non-conservative forces.
A conservative force is a force that does zero work in a closed path. If only conservative forces act on a system, the mechanical energy remains conserved. Examples of conservative forces include gravitational force and spring force. Conversely, non-conservative forces cause a loss of mechanical energy from the system. Friction, air resistance, and tension in a cord are examples of non-conservative forces. Although these forces convert mechanical energy into heat, sound, or light, they adhere to the principle that energy cannot be created or destroyed.
Work Done by a Conservative Force
When considering the work done by a conservative force, it is vital to note that it is independent of the path taken. In Figure 1, the work done by the conservative force in a closed path is zero.
In figure (1) we know work done by the conservative force in a closed path is zero.
W1, A, B + W2, B, A = 0
W1, A, B = – W2, B, A
We also have,
W2, B, A = – W2, A, B
Using the above two equations we get,
W1, A, B = W2, A, B
The above equation shows that work done to move a particle from point A to B through path 1 and 2 as shown in figure 2 will take the same amount of work done. But this statement is not valid for non-conservative forces.
Difference Between Conservative Force and Non-conservative Force
To summarize the distinctions between conservative and non-conservative forces:
Conservative Force:
- Work done (W) is the same for any closed path.
- For a closed path, the total work is zero (W = 0).
- The force is independent of the path.
- Examples include gravitational force, spring force, and electrostatic force between two electric charges.
Non-conservative Force:
- Work done (W) varies depending on the path.
- For a closed path, the total work is not zero (W ≠ 0).
- The force depends on the path.
- Examples include friction, air resistance, and tension in a cord.
Conservative Force Formula
A conservative force is characterized by the property that the work done is independent of the path taken, relying solely on the initial and final positions. It aligns with the law of conservation of energy. The formula for conservative force in relation to the conservation of kinetic energy is given by:
ΔKE= ∫ F.dr
What is Power?
Power is the measure of the amount of energy consumed or the rate at which work is performed within a specific time frame. It can be defined as the energy expended or work accomplished per unit of time.
The formula for power is given by Power = Work done/Time taken.
The unit of power is the watt.
Example: Let's consider the scenario of a lift motor moving a fully laden lift a distance of 4m between floors within a time frame of 1.5s.
The lift has a mass of 1850 kg (ignoring friction).
a) Calculate the weight of the fully laden lift.
Weight (W) = mass (m) × acceleration due to gravity (g) = 1850 kg × 10 m/s² = 18500 N.
b) What is the upward force in the cable when the lift is moving at a constant speed?
When the lift is moving at a constant speed, the forces must be balanced. Therefore, the upward force is equal to the downward force (weight). Hence, the upward force is 18500 N.
c) What is the work done by the motor?
Work done (W) = force (F) × distance (d) = 18500 N × 4 m. Therefore, the work done is 74000 J (joules).
d) What is the minimum power of the motor to raise the lift at a steady speed?
Steady speed implies balanced forces.
Power = work done/time = 74000 J / 1.5 s.
Therefore, the minimum power of the motor required to raise the lift at a steady speed is 49333 W (watts).
Difference Between Force and Power
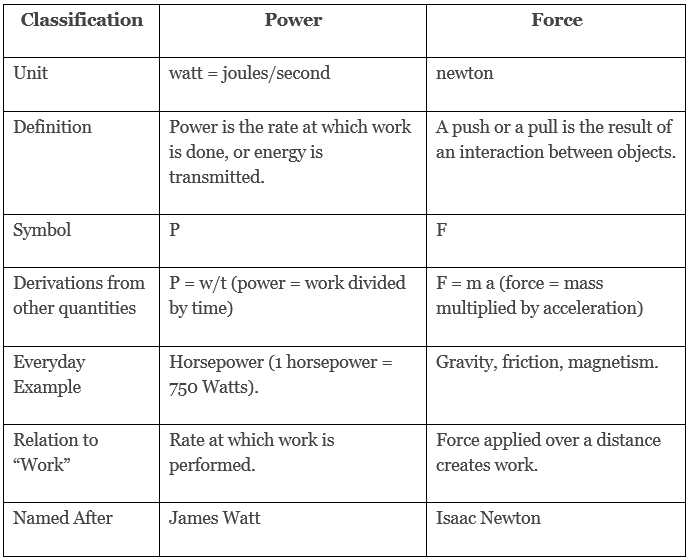
The Relation Between Force and Power
Also, power and force are related to each other.
We know that power is work done per unit time and it is expressed as:
P = W/ΔT
Work can be said as the force which is applied to make the object move, and it is expressed as:
W = FΔx
Therefore, the relation between force and power is given as:
P = FΔx/ΔT
Equilibrium
A body is said to be in translatory equilibrium if the net force acting on the body is zero,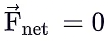
If the force are conservative then F = - dU/dr
For equilibrium F = 0.
So, - dU/dr = 0
Or
dU/dr = 0
At equilibrium position slope of U-r graph is zero or the potential energy is optimum (maximum or minimum or constant).
Types of Equilibrium
Equilibrium can be classified into three distinct types: stable equilibrium, unstable equilibrium, and neutral equilibrium. Let's explore each type in detail.
- Stable Equilibrium: When a particle is slightly displaced from its equilibrium position and it tends to return back towards equilibrium, it is considered to be in stable equilibrium. This means that there is a net restoring force acting on the body, which counteracts the displacement and brings the body back to its original position. Imagine a ball placed inside a smooth spherical shell. When displaced, it will eventually roll back to its equilibrium position due to the stable equilibrium it experiences.
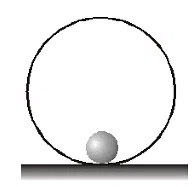 Stable Equilibrium
Stable Equilibrium
- Unstable Equilibrium: Contrary to stable equilibrium, unstable equilibrium occurs when a particle is displaced from its equilibrium position and tends to move away from it. In this case, the net force acting on the body drives it further from its original position. Picture a ball perched atop a smooth sphere. Even the slightest disturbance will cause the ball to roll away from its equilibrium position, illustrating the nature of unstable equilibrium.
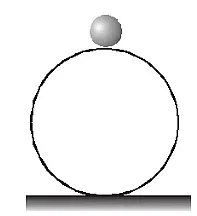 Unstable Equilibrium
Unstable Equilibrium
- Neutral Equilibrium: Neutral equilibrium occurs when a particle is displaced from its equilibrium position, but no force acts on it to bring it back or move it away. In this scenario, the body remains in its new position without any tendency to restore or alter its location. Consider a ball placed on smooth horizontal ground. If it is slightly displaced, it will stay in its new position without any force acting upon it. This exemplifies neutral equilibrium.
 Neutral Equilibrium
Neutral Equilibrium
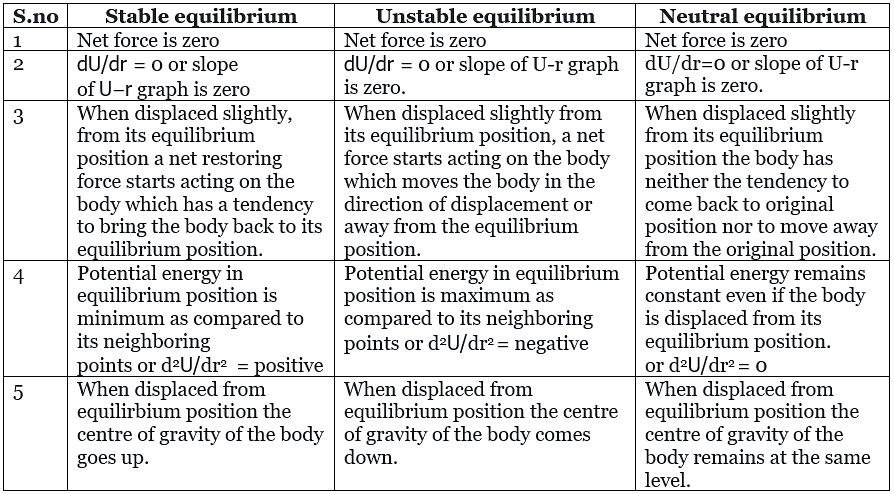
Difference Between Stable, Unstable, and Neutral Equilibrium
|
297 videos|948 docs|172 tests
|
FAQs on Types of Forces, Power and Equilibrium - Physics for JEE Main & Advanced
| 1. What is the work done by a conservative force? |  |
| 2. What is the difference between a conservative force and a non-conservative force? |  |
| 3. What is the formula for a conservative force? |  |
| 4. What is power and how does it differ from force? |  |
| 5. What are the types of equilibrium? |  |
















