Class 8 Exam > Class 8 Notes > RD Sharma Solutions for Class 8 Mathematics > RD Sharma Solutions for Class 8 Math Chapter 7 - Factorization (Part-5)
RD Sharma Solutions for Class 8 Math Chapter 7 - Factorization (Part-5) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Factorize each of the following expression:
16x2 − 25y2
Answer 1: 16x2−25y2
=(4x)2−(5y)2=(4x−5y)(4x+5y)Question 2: Factorize each of the following expression:
27x2 − 12y2
Answer 2: 27x2−12y2
=3(9x2−4y2)
=3[(3x)2−(2y)2]
=3(3x−2y)(3x+2y)
Question 3: Factorize each of the following expression:
144a2 − 289b2
Answer 3: 144a2−289b2
=(12a)2−(17b)2
=(12a−17b)(12a+17b)
Question 4: Factorize each of the following expression:
12m2 − 27
Answer 4: 12m2−27
=3(4m2−9)
=3[(2m)2−32]
=3(2m−3)(2m+3)
Question 5: Factorize each of the following expression:
125x2 − 45y2
Answer 5: 125x2−45y2
=5(25x2−9y2)
=5[(5x)2−(3y)2]
=5(5x−3y)(5x+3y)
Question 6: Factorize each of the following expression:
144a2 − 169b2
Answer 6: 144a2−169b2
=(12a)2−(13b)2
=(12a−13b)(12a+13b)
Question 7: Factorize each of the following expression:
(2a − b)2 − 16c2
Answer 7: (2a−b)2−16c2
=(2a−b)2−(4c)2
=[(2a−b)−4c][(2a−b)+4c]
=(2a−b−4c)(2a−b+4c)
Question 8: Factorize each of the following expression:
(x + 2y)2 − 4(2x − y)2
Answer 8: (x+2y)2−4(2x−y)2=(x+2y)2−[2(2x−y)]2
=[(x+2y)−2(2x−y)][(x+2y)+2(2x−y)]
=(x+2y−4x+2y)(x+2y+4x−2y)
=5x(4y−3x)
Question 9: Factorize each of the following expression:
3a5 − 48a3
Answer 9: 3a5−48a3
=3a3(a2−16)=3a3(a2−42) =3a3(a−4)(a+4)
Question 10: Factorize each of the following expression:
a4 − 16b4
Answer 10: a4−16b4=a4−24b4=(a2)2−(22b2)2
=(a2−22b2)(a2+22b2)
=[a2−(2b)2](a2+4b2)
=(a−2b)(a+2b)(a2+4b2)
Question 11: Factorize each of the following expression:
x8 − 1
Answer 11: x8−1
=(x4)2−12
=(x4−1)(x4+1)
=[(x2)2−12](x4+1)
=(x2−1)(x2+1)(x4+1)
=(x2−12)(x2+1)(x4+1)
=(x−1)(x+1)(x2+1)(x4+1)
Question 12: Factorize each of the following expression:
64 − (a + 1)2
Answer 12: 64−(a+1)2
=(8)2−(a+1)2
=[8−(a+1)][8+(a+1)]
=(8−a−1)(8+a+1)
=(7−a)(9+a)
Question 13: Factorize each of the following expression:
36l2 − (m + n)2
Answer 13: 36l2−(m+n)2
=(6l)2−(m+n)2
=[6l−(m+n)][6l+(m+n)]
=(6l−m−n)(6l+m+n)
Question 14: Factorize each of the following expression:
25x4y4 − 1
Answer 14: 25x4y4−1
=(5x2y2)2−1
=(5x2y2−1)(5x2y2+1)
Question 15: Factorize each of the following expression:
a4− 1/b4
Answer 15: a4 - 1/b4
= (a2)2 - 1/(b2)2
= a2- 1/b2a2 + 1/b2
= a - 1/ba + 1/ba2 + 1/b2
Question 16: Factorize each of the following expression:
x3 − 144x
Answer 16: x3−144x
=x(x2−144)
=x(x2−122)
=x(x−12)(x+12)
Question 17: Factorize each of the following expression:
(x - 4y)2 − 625
Answer 17: (x−4y)2−625
=(x−4y)2−252
=[(x−4y)−25][(x−4y)+25]
=(x−4y−25)(x−4y+25)
Question 18: Factorize each of the following expression:
9(a − b)2 − 100(x − y)2
Answer 18: 9(a−b)2−100(x−y)2
=[3(a−b)]2−[10(x−y)]2
=[3(a−b)−10(x−y)][3(a−b)+10(x−y)]
=(3a−3b−10x+10y)(3a−3b+10x−10y)
Question 19: Factorize each of the following expression:
(3 + 2a)2 − 25a2
Answer 19: (3+2a)2−25a2
=(3+2a)2−(5a)2
=[(3+2a)−5a][(3+2a)+5a]
=(3+2a−5a)(3+2a+5a)
=(3−3a)(3+7a)
=3(1−a)(3+7a)
Question 20: Factorize each of the following expression:
(x + y)2 − (a − b)2
Answer 20: (x+y)2−(a−b)2
=[(x+y)−(a−b)][(x+y)+(a−b)]
=(x+y−a+b)(x+y+a−b)
Question 21: Factorize each of the following expression:
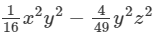
Answer 21:
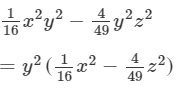
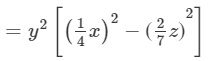
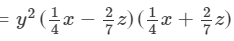
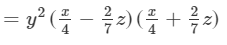
Question 22: Factorize each of the following expression:
75a3b2 - 108ab4
Answer 22: 75a3b2−108ab4
=3ab2(25a2−36b2)
=3ab2[(5a)2−(6b)2]
=3ab2(5a−6b)(5a+6b)
Question 23: Factorize each of the following expression:
x5 − 16x3
Answer 23: x5−16x3
=x3(x2−16)
=x3(x2−42)
=x3(x−4)(x+4)
Question 24: Factorize each of the following expression:
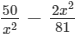
Answer 24:
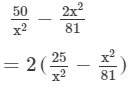
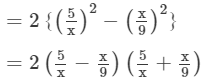
Question 25: Factorize each of the following expression:
256x5 − 81x
Answer 25: 256x5−81x
=x(256x4−81)
=x[(16x2)2−92]
=x(16x2+9)(16x2−9)
=x(16x2+9)[(4x)2−32]
=x(16x2+9)(4x+3)(4x−3)
Question 26: Factorize each of the following expression:
a4 − (2b + c)4
Answer 26: a4−(2b+c)4
=(a2)2−[(2b+c)2]2
=[a2+(2b+c)2][a2−(2b+c)2]
=[a2+(2b+c)2]{[a+(2b+c)][a−(2b+c)]}
=[a2+(2b+c)2](a+2b+c)(a−2b−c)
Question 27: Factorize each of the following expression:
(3x + 4y)4 − x4
Answer 27: (3x+4y)4−x4
=[(3x+4y)2]2−(x2)2
=[(3x+4y)2+x2][(3x+4y)2−x2]
=[(3x+4y)2+x2][(3x+4y)+x][(3x+4y)−x]
={(3x+4y)2+x2}(3x+4y+x)(3x+4y−x)
={(3x+4y)2+x2}(4x+4y)(2x+4y)
={(3x+4y)2+x2}4(x+y)2(x+2y)
=8{(3x+4y)2+x2}(x+y)(x+2y)
Question 28: Factorize each of the following expression:
p2q2 − p4q4
Answer 28: p2q2−p4q4
=p2q2(1−p2q2)
=p2q2[1−(pq)2]
=p2q2(1−pq)(1+pq)
Question 29: Factorize each of the following expression:
3x3y − 243xy3
Answer 29: 3x3y−243xy3
=3xy(x2−81y2)
=3xy[x2−(9y)2]
=3xy(x−9y)(x+9y)
Question 30: Factorize each of the following expression:
a4b4 − 16c4
Answer 30: a4b4−16c4
=[(a2b2)2−(4c2)2]
=(a2b2+4c2)(a2b2−4c2)
=(a2b2+4c2)[(ab)2−(2c)2]
=(a2b2+4c2)(ab+2c)(ab−2c)
Question 31: Factorize each of the following expression:
x4 − 625
Answer 31: x4−625
=(x2)2−252
=(x2+25)(x2−25)
=(x2+25)(x2−52)
=(x2+25)(x+5)(x−5)
Question 32: Factorize each of the following expression:
x4 − 1
Answer 32: x4−1
=(x2)2−1
=(x2+1)(x2−1)
=(x2+1)(x+1)(x−1)
Question 33: Factorize each of the following expression:
49(a − b)2 − 25(a + b)2
Answer 33: 49(a−b)2−25(a+b)2
=[7(a−b)]2−[5(a+b)]2
=[7(a−b)−5(a+b)][7(a−b)+5(a+b)]
=(7a−7b−5a−5b)(7a−7b+5a+5b)
=(2a−12b)(12a−2b)
=2(a−6b)2(6a−b)
=4(a−6b)(6a−b)
Question 34: Factorize each of the following expression:
x − y − x2 + y2
Answer 34: x−y−x2+y2
=(x−y)+(y2−x2) [Regrouping the terms]
=(x−y)+(y+x)(y−x)
=(x−y)−(y+x)(x−y) [∵(y−x)=−(x−y)]
=(x−y)[1−(y+x)]
=(x−y)(1−x−y)
Question 35: Factorize each of the following expression:
16(2x − 1)2 − 25y2
Answer 35: 16(2x−1)2−25y2
=[4(2x−1)]2−(5y)2
=[4(2x−1)−5y][4(2x−1)+5y]
=(8x−4−5y)(8x−4+5y)
=(8x−5y−4)(8x+5y−4)
Question 36: Factorize each of the following expression:
4(xy + 1)2 − 9(x − 1)2
Answer 36: 4(xy+1)2−9(x−1)2
=[2(xy+1)]2−[3(x−1)]2
=[2(xy+1)−3(x−1)][2(xy+1)+3(x−1)]
=(2xy+2−3x+3)(2xy+2+3x−3)
=(2xy−3x+5)(2xy+3x−1)
Question 37: Factorize each of the following expression:
(2x + 1)2 − 9x4
Answer 37: (2x+1)2−9x4
=(2x+1)2−(3x2)2
=[(2x+1)−3x2][(2x+1)+3x2]
=(−3x2+2x+1)(3x2+2x+1)
We can factorise the quadratic expressions in the curved brackets as: (−3x2+3x−x+1)(3x2+2x+1)
={3x(−x+1)+1(−x+1)}(3x2+2x+1)
=(−x+1)(3x+1)(3x2+2x+1)
=−(x−1)(3x+1)(3x2+2x+1)
Question 38: Factorize each of the following expression:
x4 − (2y − 3z)2
Answer 38: x4−(2y−3z)2
=(x2)2−(2y−3z)2
=[x2−(2y−3z)][x2+(2y−3z)]
=(x2−2y+3z)(x2+2y−3z)
Question 39: Factorize each of the following expression:
a2 − b2 + a − b
Answer 39: a2−b2+a−b=(a2−b2)+(a−b) [Grouping the terms]
=(a+b)(a−b)+(a−b)
=(a−b)(a+b+1) [Taking out the common factor (a−b)]
Question 40: Factorize each of the following expression:
16a4 − b4
Answer 40: 16a4−b4
=(4a2)2−(b2)2
=(4a2+b2)(4a2−b2)
=(4a2+b2)[(2a)2−b2]
=(4a2+b2)(2a+b)(2a−b)
Question 41: Factorize each of the following expression:
a4 − 16(b − c)4
Answer 41: a4−16(b−c)4
=(a2)2−[4(b−c)2]2
=[a2+4(b−c)2][a2−4(b−c)2]
=[a2+4(b−c)2]{a2−[2(b−c)]2}
=[a2+4(b−c)2][a+2(b−c)][a−2(b−c)]
=[a2+4(b−c)2](a+2b−2c)(a−2b+2c)
Question 42: Factorize each of the following expression:
2a5 − 32a
Answer 42: 2a5−32a
=2a(a4−16)
=2a[(a2)2−42]
=2a(a2+4)(a2−4)
=2a(a2+4)(a2−22)
=2a(a2+4)(a+2)(a−2)
=2a(a−2)(a+2)(a2+4)
Question 43: Factorize each of the following expression:
a4b4 − 81c4
Answer 43: a4b4−81c4
=(a2b2)2−(9c2)2
=(a2b2+9c2)(a2b2−9c2)
=(a2b2+9c2)[(ab)2−(3c)2]
=(a2b2+9c2)(ab+3c)(ab−3c)
Question 44: Factorize each of the following expression:
xy9 − yx9
Answer 44: xy9−yx9
=xy(y8−x8)
=xy[(y4)2−(x4)2]
=xy(y4+x4)(y4−x4)=xy(y4+x4)[(y2)2−(x2)2]
=xy(y4+x4)(y2+x2)(y2−x2)
=xy(y4+x4)(y2+x2)(y+x)(y−x)
Question 45: Factorize each of the following expression:
x3 − x
Answer 45: x3−x
=x(x2−1)
=x(x−1)(x+1)
Question 46: Factorize each of the following expression:
18a2x2 − 32
Answer 46: 18a2x2−32
=2(9a2x2−16)
=2[(3ax)2−42]
=2(3ax−4)(3ax+4)
The document RD Sharma Solutions for Class 8 Math Chapter 7 - Factorization (Part-5) | RD Sharma Solutions for Class 8 Mathematics is a part of the Class 8 Course RD Sharma Solutions for Class 8 Mathematics.
All you need of Class 8 at this link: Class 8
Related Searches
















