Chapter 22 - Mensuration - III (Part - 2), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 22.25:
Question 1:
Find the volume of a cylinder whose
(i) r = 3.5 cm, h = 40 cm
(ii) r = 2.8 m, h = 15 m
ANSWER:
(i) Given :r = 3.5 cm, h = 40 cm
Volume of cylinder, V = πr²h = 22/7× (3.5)2 × 40 = 1540 cm³
(ii) Given:r = 2.8 m, h = 15 m
Volume of cylinder, V = πr²h = 22/7× (2.8)2 × 15 = 369.6 m³
Question 2:
Find the volume of a cylinder, if the diameter (d) of its base and its altitude (h) are:
(i) d = 21 cm, h = 10 cm
(ii) d = 7 m, h = 24 m
ANSWER:
(i) Given:d = 21 cm, radius, r = d/2 = 10.5 cm height, h = 10 cm
Volume of the cylinder, V = πr²h = 22/7× (10.5)2 × 10 = 3465 cm³
(ii) Given: d = 7 m, radius, r = d/2 = 3.5 m height h = 24 m
Volume of the cylinder, V = πr²h = 22/7× (3.5)2 × 24 = 924 m³
Question 3:
The area of the base of a right circular cylinder is 616 cm² and its height is 25 cm. Find the volume of the cylinder.
ANSWER:
Let the area of the base of a right circular cylinder be S cm².
Given:S = 616 cm²
Height, h = 25 cm
Let the radius of a right circular cylinder be r cm. S = πr2
616 = 22/7× r2
r2 = (616 × 7)/22
r2 = 196 r = 14 cm
Volume of the cylinder, V = πr²h = π × (14)2 × 25 = 15400 cm³
Question 4:
The circumference of the base of a cylinder is 88 cm and its height is 15 cm. Find the volume of the cylinder.
ANSWER:
Let r cm be the radius of a cylinder.Circumference of the cylinder, S = 2πr
Given:Height, h = 15 cm
Circumference, S = 88 cm S = 2πr
88 = 2 × 22/7× r
r = (88 × 7)/44
r = 14 cm
Volume of cylinder, V = πr²h = 22/7× 142 × 15 = 9240 cm³
Question 5:
A hollow cylindrical pipe is 21 dm long. Its outer and inner diameters are 10 cm and 6 cm respectively. Find the volume of the copper used in making the pipe.
ANSWER:
Let the length of the cylinder pipe be h = 21, dm = 210 cm.
Let the outer and the inner radius of the pipe be R cm and r cm, respectively.
∴ 2R = 10 and 2
r = 6R = 5 cm and r = 3cm
Volume of the copper used in making the pipe, V = π(R2−r2)h
= 22/7× (52−32) × 210
= 22 × (25−9) × 30
= 22 × 16 × 30 = 10560 cm³
Question 6:
Find the (i) curved surface area (ii) total surface area and (iii) volume of a right circular cylinder whose height is 15 cm and the radius of the base is 7 cm.
ANSWER:
Given:Height, h = 15 cm
Radius, r = 7 cm
(i) Curved surface area, S1 = 2πrh
= 2 × 22/7× 7 × 15
= 660 cm²
(ii) Total surface area, S2 = 2πr(r+h)
= 2 × 22/7× 7 × (7+15) = 44 × 22
= 968 cm²
(iii) Volume of the right circular cylinder, V = πr²h
= 22/7× 72 × 15
= 2310 cm³
Question 7:
The diameter of the base of a right circular cylinder is 42 cm and its height is 10 cm. Find the volume of the cylinder.
ANSWER:
Given:Diameter, d = 42 cm
Radius, r = d/2 = 21 cm
Height, h = 10 cm
Volume of the cylinder, V = πr²h
= 22/7× 212 × 10
= 13860 cm³
Question 8:
Find the volume of a cylinder, the diameter of whose base is 7 cm and height being 60 cm. Also, find the capacity of the cylinder in litres.
ANSWER:
Given:Diameter, d = 7 cm
Radius, r = 3.5 cm
Height, h = 60 cm
Volume of the cylinder, V = πr²h
= 22/7× 3.52 × 60
= 2310 cm³
Capacity of the cylinder in liters = 2310/1000 ( 1 litre = 1000 cubic cm) = 2.31 L
Question 9:
A rectangular strip 25 cm × 7 cm is rotated about the longer side. Find the volume of the solid, thus generated.
ANSWER:
Given:Rectangular strip has radius, r = 7 cm
Height, h = 25 cm
Volume of the solid, V = πr²h = 22/7× 72 × 25 = 3850 cm³
Question 10:
A rectangular sheet of paper, 44 cm × 20 cm, is rolled along its length to form a cylinder. Find the volume of the cylinder so formed.
ANSWER:
The length (l) and breadth (b) of the rectangular sheet are 44 cm and 20 cm
Now, the sheet is rolled along the length to form a cylinder.Let the radius of the cylinder be r cm.Height, h = b = 20 cm
Circumference, S = 44 cm
2πr = 44 cm² × 22/7× r = 44 cm
r = 7 cm
Volume of the cylinder, V = πr²h
= 22/7× 72 × 20 cm³
= 3080 cm³
Question 11:
The volume and the curved surface area of a cylinder are 1650 cm³ and 660 cm² respectively. Find the radius and height of the cylinder.
ANSWER:
Curved surface area of the cylinder = 2πrh = 660 cm² ... (1)
Volume of the cylinder = πr²h = 1650 cm³ ... (2)
From (1) and (2), we can calculate the radius (r) and the height of cylinder (h).
We know the volume of the cylinder, i.e. 1650 cm³
∴ 1650 = πr²h
h = 1650πr²
h = 1650/πr2
Substituting h into (1):
660 = 2πrh
660 = 2πr × 1650/πr2
660r = 2(1650)
r = 5 cm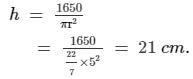
Hence, the radius and the height of the cylinder are 5 cm and 21 cm, respectively.
Question 12:
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. Calculate the ratio of their volumes.
ANSWER:
Here, r1 = Radius of cylinder 1
h1 = Height of cylinder 1
r2 = Radius of cylinder 2
h2 = Height of cylinder 2
V1 = Volume of cylinder 1
V2 = Volume of cylinder 2
Ratio of the radii of two cylinders = 2:3
Ratio of the heights of two cylinders = 5:3
Volume of the cylinder = πr²h
V1/V2 = (πr12h1)/(πr22h2) = (π(2r)25h)/(π(3r)23h)
V1/V2 = (π4r25h)/(π9r23h) = 20 / 27
Hence, the ratio of their volumes is 20:27
Question 13:
The ratio between the curved surface area and the total surface area of a right circular cylinder is 1 : 2. Find the volume of the cylinder, if its total surface area is 616 cm².
ANSWER:
Let r cm be the radius and h cm be the length of the cylinder. The curved surface area and the total surface area is 1:2.
The total surface area is 616 cm².
The curved surface area is the half of 616 cm², i.e. 308 cm².
Curved area = 2πrh
So, h = 308/2πr
Total surface area = Curved surface area + Top and bottom area
Top and bottom area = 616 - 308 = 308 cm² = 2πr2
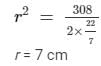
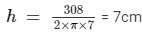
Then, the volume of the cylinder can be calculated as follows:
V = 22/7× 72 × 7 = 1078
Hence, it is obtained that the volume of the cylinder is 1078 cm³.
Question 14:
The curved surface area of a cylinder is 1320 cm² and its base has diameter 21 cm. Find the volume of the cylinder.
ANSWER:
r cm = Radius of the cylinder
h cm = Height of the cylinder
Diameter of the cylinder is 21 cm. Thus, the radius is 10.5 cm.
Since the curved surface area has been known, we can calculate h by the equation given below:
The curved surface area of the cylinder = 2πrh
1320 cm² = 2πrh
1320 cm² = 2 x 22/7 x (10.5 cm) x h
h = 20 cm
∴ Volume of the cylinder (V) = πr²h
V = 22/7(10.5 cm)2(20 cm)
V = 6930 cm³
Question 15:
The ratio between the radius of the base and the height of a cylinder is 2 : 3. Find the total surface area of the cylinder, if its volume is 1617 cm³.
ANSWER:
Let r cm be the radius and h cm be the height of the cylinder. It is given that the ratio of r and h is 2:3, so h = 1.5r
The volume of the cylinder (V) is 1617 cm³.
So, we can find the radius and the height of the cylinder from the equation given below:
V = πr²h
1617 = πr²h
1617 = πr2(1.5r)
r3 = 343
r = 7 cm and h = 10.5 cm
Total surface area = 2πr2+2πrh
= 2 × 22/7 × 72 + 2 × 22/7 × 7 × 10.5 = 770 cm²
Hence, the total surface area of the cylinder is 770 cm².
Question 16:
The curved surface area of a cylindrical pillar is 264 m2 and its volume is 924 m³. Find the diameter and the height of the pillar.
ANSWER:
Here, r m = radius of the cylinder
h m = height of the cylinder
Curved surface area of the cylinder = 2πrh ... (1)
Volume of the cylinder = πr²h ... (2)
924 = πr²h
h = 924/πr²
Then, substitute h into equation (1):
264 = 2πrh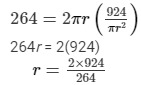
r = 7 m, so d = 14 m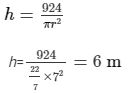
Hence, the diameter and the height of the cylinder are 14 m and 6 m, respectively.
Question 17:
Two circular cylinders of equal volumes have their heights in the ratio 1 : 2. Find the ratio of their radii.
ANSWER:
Here, V1 = Volume of cylinder 1
V2 = Volume of cylinder 2
r1 = Radius of cylinder 1
r2 = Radius of cylinder 2
h1 = Height of cylinder 1
h2 = Height of cylinder 2
Volumes of cylinder 1 and 2 are equal.
Height of cylinder 1 is half the height of cylinder 2.
∴ V1 = V2
(πr12h1) = (πr22h2)
(πr12h) = (πr222h)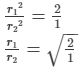
Thus, the ratio of their radii is √2 : 1.
Question 18:
The height of a right circular cylinder is 10.5 m. Three times the sum of the areas of its two circular faces is twice the area of the curved surface. Find the volume of the cylinder.
ANSWER:
It is known that three times the sum of the areas of the two circular faces, of the right circular cylinder, is twice the area of the curved surface.
Hence, it can be written using the following formula:
3 (2πr2) = 2(2πrh)
3πr2 = 2πrh
3r = 2h
It is known that the height of the cylinder (h) is 10.5 m.
Substituting this number in the equation:
3r = 2(10.5)
r = 7 m
Volume of the cylinder = πr²h
= 22/7(72) (10.5)
= 1617 m³
Thus, the volume of the cylinder is 1617 m³.
Question 19:
How many cubic meters of earth must be dug-out to sink a well 21 m deep and 6 m diameter?
ANSWER:
The volume of the earth that must be dug out is similar to the volume of the cylinder which is equal to πr²h.
Height of the well = 21 m
Diameter of the well = 6 m
∴ Volume of the earth that must be dug out = (π (32) (21)) m³ = 594 m³
FAQs on Chapter 22 - Mensuration - III (Part - 2), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What are the different types of mensuration problems covered in RD Sharma Solutions Chapter 22? |  |
| 2. How can I find the surface area of a cube using the formula given in RD Sharma Solutions Chapter 22? |  |
| 3. What is the formula for finding the volume of a cylinder as mentioned in RD Sharma Solutions Chapter 22? |  |
| 4. How can I calculate the volume of a cone using the formula provided in RD Sharma Solutions Chapter 22? |  |
| 5. What is the formula for finding the volume of a sphere as mentioned in RD Sharma Solutions Chapter 22? |  |





















