RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-5) | RD Sharma Solutions for Class 8 Mathematics PDF Download
Question 1: Making use of the cube root table, find the cube roots 7
Answer 1: Because 7 lies between 1 and 100, we will look at the row containing 7 in the column of x.
By the cube root table, we have:
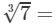 1.913
1.913
Thus, the answer is 1.913.
Question 2: Making use of the cube root table, find the cube root 70
Answer 2: Because 70 lies between 1 and 100, we will look at the row containing 70 in the column of x.
By the cube root table, we have:
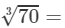 4.121
4.121
Question 3: Making use of the cube root table, find the cube root 700
Answer 3: We have:
700=70×10700=70×10
∴∴ Cube root of 700 will be in the column of 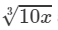 against 70.
against 70.
By the cube root table, we have:
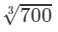 =8.879
=8.879
Thus, the answer is 8.879.
Question 4: Making use of the cube root table, find the cube root 7000
Answer 4: We have:
7000=70×1007000=70×100
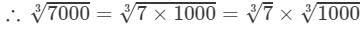
By the cube root table, we have:
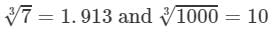
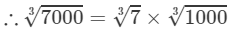 =1.913×10=19.13
=1.913×10=19.13
Question 5: Making use of the cube root table, find the cube root 1100
Answer 5: We have:
1100=11×1001100=11×100
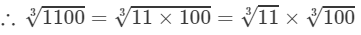
By the cube root table, we have:
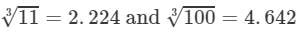
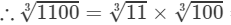 =2.224×4.642=10.323 (Up to three decimal places)11003=113×1003=2.224×4.642=10.323 (Up to three decimal places)
=2.224×4.642=10.323 (Up to three decimal places)11003=113×1003=2.224×4.642=10.323 (Up to three decimal places)
Thus, the answer is 10.323.
Question 6: Making use of the cube root table, find the cube root 780
Answer 6: We have:
780=78×10780=78×10
∴∴ Cube root of 780 would be in the column of 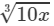 against 78.
against 78.
By the cube root table, we have:
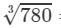 = 9.205
= 9.205
Thus, the answer is 9.205.
Question 7: Making use of the cube root table, find the cube root 7800
Answer 7: We have:
7800=78×1007800=78×100
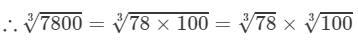
By the cube root table, we have:
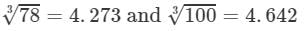
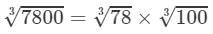 =4.273×4.642=19.835 (upto three decimal places)
=4.273×4.642=19.835 (upto three decimal places)
Thus, the answer is 19.835
Question 8: Making use of the cube root table, find the cube root 1346
Answer 8: By prime factorisation, we have:
1346=2×673⇒ 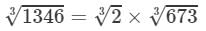
Also
670<673<680⇒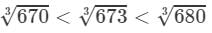
From the cube root table, we have:
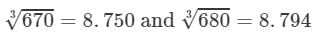
For the difference (680−-670), i.e., 10, the difference in the values
=8.794−8.750=0.044=8.794-8.750=0.044
∴∴ For the difference of (673−-670), i.e., 3, the difference in the values
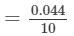 ×3=0.0132=0.013=0.04410×3=0.0132=0.013 (upto three decimal places)
×3=0.0132=0.013=0.04410×3=0.0132=0.013 (upto three decimal places)
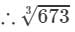 =8.750+0.013=8.7636733=8.750+0.013=8.763
=8.750+0.013=8.7636733=8.750+0.013=8.763
Now
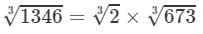 =1.260×8.763=11.04113463=23×6733=1.260×8.763=11.041 (upto three decimal places)
=1.260×8.763=11.04113463=23×6733=1.260×8.763=11.041 (upto three decimal places)
Thus, the answer is 11.041.
Question 9: Making use of the cube root table, find the cube root 250
Answer 9: We have:
250=25×100250=25×100
∴∴ Cube root of 250 would be in the column of 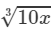 against 25.
against 25.
By the cube root table, we have:
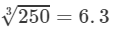
Thus, the required cube root is 6.3.
Question 10: Making use of the cube root table, find the cube root 5112
Answer 10: By prime factorisation, we have:
5112=23×32×71⇒ 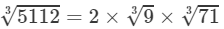
By the cube root table, we have:
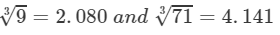
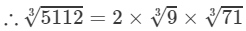 =2×2.080×4.141=17.22751123=2×93×713=2×2.080×4.141=17.227 (upto three decimal places)
=2×2.080×4.141=17.22751123=2×93×713=2×2.080×4.141=17.227 (upto three decimal places)
Thus, the required cube root is 17.227.
Question 11: Making use of the cube root table, find the cube root
9800
Answer 11: We have:
9800=98×1009800=98×100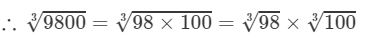
By cube root table, we have:
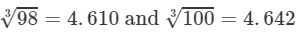
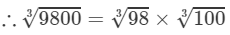 =4.610×4.642=21.4098003=983×1003=4.610×4.642=21.40 (upto three decimal places)
=4.610×4.642=21.4098003=983×1003=4.610×4.642=21.40 (upto three decimal places)
Thus, the required cube root is 21.40.
Question 12: Making use of the cube root table, find the cube root 732
Answer 12: We have:
730<732<740⇒ 
From cube root table, we have:

For the difference (740−-730), i.e., 10, the difference in values
=9.045−9.004=0.041=9.045-9.004=0.041
∴∴ For the difference of (732−-730), i.e., 2, the difference in values
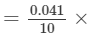 2=0.0082
2=0.0082
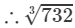 =9.004+0.008=9.012
=9.004+0.008=9.012
Question 13: Making use of the cube root table, find the cube root 7342
Answer 13: We have:
7300<7342<7400⇒ 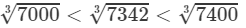
From the cube root table, we have:
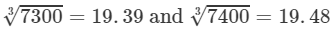
For the difference (7400−-7300), i.e., 100, the difference in values
=19.48−19.39=0.09
∴∴ For the difference of (7342−-7300), i.e., 42, the difference in the values
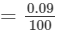 ×42=0.0378=0.037
×42=0.0378=0.037
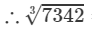 =19.39+0.037=19.427
=19.39+0.037=19.427
Question 14: Making use of the cube root table, find the cube root 133100
Answer 14: We have:
133100=1331×100⇒ 
By cube root table, we have:
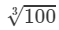 =4.6421003=4.642
=4.6421003=4.642
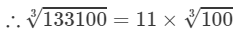 =11×4.642=51.062
=11×4.642=51.062
Question 15: Making use of the cube root table, find the cube root 37800
Answer 15: We have:
37800=23×33×175⇒ 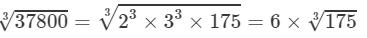
Also
170<175<180⇒ 
From cube root table, we have:
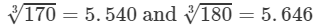
For the difference (180−-170), i.e., 10, the difference in values
=5.646−5.540=0.106=5.646-5.540=0.106
∴∴ For the difference of (175−-170), i.e., 5, the difference in values
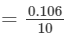 ×5=0.053=0.10610×5=0.053
×5=0.053=0.10610×5=0.053
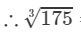 =5.540+0.053=5.5931753=5.540+0.053=5.593
=5.540+0.053=5.5931753=5.540+0.053=5.593
Now
37800=6×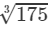 =6×5.593=33.55837800=6×1753=6×5.593=33.558
=6×5.593=33.55837800=6×1753=6×5.593=33.558
Thus, the required cube root is 33.558.
Question 16: Making use of the cube root table, find the cube root 0.27
Answer 16: The number 0.27 can be written as 27/100.
Now
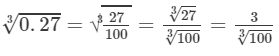
By cube root table, we have:
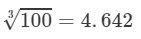
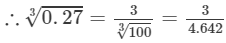
=0.6460.273=31003=34.642=0.646.
Thus, the required cube root is 0.646.
Question 17: Making use of the cube root table, find the cube root 8.6
Answer 17: The number 8.6 can be written as 86/10.
Now
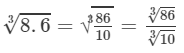
By cube root table, we have:
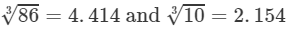
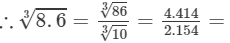 2.0498.63=863103=4.4142.154=2.049
2.0498.63=863103=4.4142.154=2.049
Thus, the required cube root is 2.049.
Question 18: Making use of the cube root table, find the cube root 0.86
Answer 18: The number 0.86 could be written as 86/100.
Now
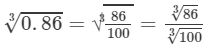
By cube root table, we have:
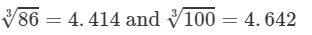
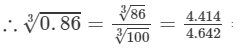 =0.9510.863=8631003=4.4144.642=0.951 (upto three decimal places)
=0.9510.863=8631003=4.4144.642=0.951 (upto three decimal places)
Thus, the required cube root is 0.951.
Question 19: Making use of the cube root table, find the cube root 8.65
Answer 19: The number 8.65 could be written as 865/100.
Now
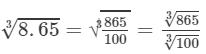
Also
860<865<870⇒ 
From the cube root table, we have:
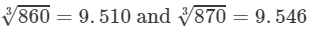
For the difference (870−-860), i.e., 10, the difference in values
=9.546−9.510=0.036=9.546-9.510=0.036
∴∴ For the difference of (865−-860), i.e., 5, the difference in values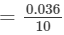 ×5=0.018 (upto three decimal places)
×5=0.018 (upto three decimal places)
 9.510+0.018=9.5288653=9.510+0.018=9.528 (upto three decimal places)
9.510+0.018=9.5288653=9.510+0.018=9.528 (upto three decimal places)
From the cube root table, we also have:
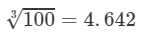
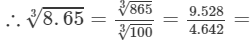 2.0538.653=86531003=9.5284.642=2.053 (upto three decimal places)
2.0538.653=86531003=9.5284.642=2.053 (upto three decimal places)
Thus, the required cube root is 2.053.
Question 20: Making use of the cube root table, find the cube root 7532
Answer 20: We have:
7500<7532<7600⇒ 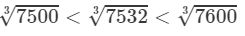
From the cube root table, we have:
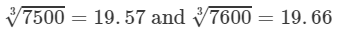
For the difference (7600−-7500), i.e., 100, the difference in values
=19.66−19.57=0.09=19.66-19.57=0.09
∴∴ For the difference of (7532−-7500), i.e., 32, the difference in values
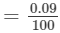 ×32=0.0288=0.029=0.09100×32=0.0288=0.029 (up to three decimal places)
×32=0.0288=0.029=0.09100×32=0.0288=0.029 (up to three decimal places)
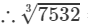 =19.57+0.029=19.59975323=19.57+0.029=19.599
=19.57+0.029=19.59975323=19.57+0.029=19.599
Question 21: Making use of the cube root table, find the cube root
833
Answer 21: We have:
830<833<840⇒ 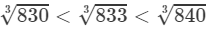
From the cube root table, we have:
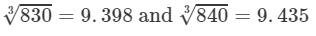
For the difference (840−-830), i.e., 10, the difference in values
=9.435−9.398=0.037=9.435-9.398=0.037
∴∴ For the difference (833−-830), i.e., 3, the difference in values
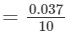 ×3=0.0111=0.011=0.03710×3=0.0111=0.011 (upto three decimal places)
×3=0.0111=0.011=0.03710×3=0.0111=0.011 (upto three decimal places)
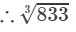 =9.398+0.011=9.4098333=9.398+0.011=9.409
=9.398+0.011=9.4098333=9.398+0.011=9.409
Question 22: Making use of the cube root table, find the cube root 34.2
Answer 22: The number 34.2 could be written as 342/10.
Now
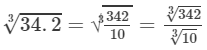
Also
340<342<350⇒ 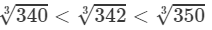
From the cube root table, we have: 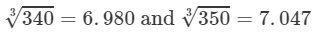
For the difference (350−-340), i.e., 10, the difference in values
=7.047−6.980=0.067=7.047-6.980=0.067.
∴∴ For the difference (342−-340), i.e., 2, the difference in values
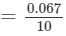 ×2=0.013=0.06710×2=0.013 (upto three decimal places)
×2=0.013=0.06710×2=0.013 (upto three decimal places)
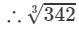 =6.980+0.0134=6.9933423=6.980+0.0134=6.993 (upto three decimal places)
=6.980+0.0134=6.9933423=6.980+0.0134=6.993 (upto three decimal places)
From the cube root table, we also have:
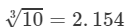
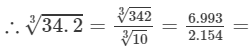 3.246
3.246
Thus, the required cube root is 3.246.
Question 23: What is the length of the side of a cube whose volume is 275 cm3. Make use of the table for the cube root.
Answer 23: Volume of a cube is given by:
V=a3V=a3, where a = side of the cube
∴∴ Side of a cube = a= 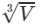
If the volume of a cube is 275 cm3, the side of the cube will be 
We have:
270<275<280⇒
From the cube root table, we have:
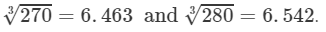
For the difference (280−-270), i.e., 10, the difference in values
=6.542−6.463=0.079=6.542-6.463=0.079
∴∴ For the difference (275−-270), i.e., 5, the difference in values
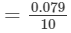 ×5=0.0395 ≃ 0.04=0.07910×5=0.0395 ≃ 0.04 (upto three decimal places)
×5=0.0395 ≃ 0.04=0.07910×5=0.0395 ≃ 0.04 (upto three decimal places)
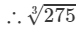 =6.463+0.04=6.5032753=6.463+0.04=6.503 (upto three decimal places)
=6.463+0.04=6.5032753=6.463+0.04=6.503 (upto three decimal places)
Thus, the length of the side of the cube is 6.503 cm.
FAQs on RD Sharma Solutions for Class 8 Math Chapter 4 - Cubes and Cube Roots (Part-5) - RD Sharma Solutions for Class 8 Mathematics
| 1. What is the formula to find the volume of a cube? |  |
| 2. How can I calculate the cube root of a number without a calculator? |  |
| 3. What is the difference between a perfect cube and a cube number? |  |
| 4. How can I find the cube root of a decimal number? |  |
| 5. Can a cube have a negative volume? |  |
















