Class 9 Maths Chapter 11 Question Answers - Surface Areas and Volumes
Q1: Shanti Sweets stall placed an order to Mr. Kishorilal for making cardboard boxes for packing their sweets. Two sizes of boxes are ordered. The bigger of dimensions 25cm × 20cm × 5cm and the smaller of dimensions 15cm × 12cm × 5cm. For all the overlaps, 5% of the total surface is required extra. 250 boxes of each kind are required. Cost of the cardboard is ₹ 4 for 1000 cm2. By mistake Shanti Sweets Stall made payment according to the bigger boxes, but Mr. Kishorilal returned back the excess money.
(a) What amount was returned back by Mr. Kishorilal to the Shanti Sweets Stall?
(b) Which mathematical concept is used in the above problem?
(c) By returning back the access money, which value is depicted by Mr. Kishorilal?
Sol.
(a) Total surface area of 250 bigger boxes
Surface area of 1 box = 2 (lb + bh + hl)
= 2 (25 × 20 + 20 × 5 + 5 × 25) cm2
= 2 (500 + 100 + 125) cm2
= 2 × 725 cm2 = 1450 cm2
∴ Surface area of 250 big boxes = 250 × 1450 cm2
= 362500 cm2
Total surface area of 250 smaller boxes :
= 2 (15×12 + 12×5 + 5×15) cm2
= 2 (180 + 60 + 75) cm2 = 630 cm2
∴ Total surface area of 250 small boxes = 250 × 630 cm2 = 157500 cm2
Total surface area of both kinds of boxes = 362500 cm2 + 157500 cm2 = 520000 cm2
Area for overlaping = 5% of 520000 cm2 = 26000 cm2
∴ Total surface area for which actual payment is to be made = 520000 cm2 + 26000 cm2 = 546000 cm2
Actual cost = (4/1000)× 546000 = ₹ 2184
But by mistake the payment is made for 500 boxes, each of dimension 25cm × 20cm × 5cm
∴ Total surface area 250 + 250 boxes for wrong payment = 500 × 2 [lb × bh × hl]
500 × 2 [25 × 20 + 20 × 5 + 5 × 25] cm2
= 500 × 1450 cm2 = 725000 cm2
Area for overlaping = 5% of 725000 = 36250 cm2
Total surface area for wrong payment = (72500 + 36250) cm2 = 761250 cm2
∴ Wrong payment made by the Shanti Sweets Stall =₹ (4/1000)× 761250 = ₹ 3045
⇒ Excess amount paid by Shanti Sweets Stall to Mr. Kishorilal = ₹ 3045 – ₹ 2184 = ₹ 861
(b) The mathematical concept used in the above problem is Surface Areas and Volumes.
(c) value is depicted by Mr. Kishorilal is Honesty.
Q2: Rahul plans to erect an indoor greenhouse (herbarium) which is made entirely of glass panes (including a base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.
(a) What is the surface area of the glass used?
(b) How much of tape is needed for all the 12 edges?
(c) Which mathematical concept is used in the above problem?
(d) By erecting a greenhouse, which skill is depicted by Rahul?
Sol: The herbarium is in the form of a cuboid, having l = 30cm, b = 25cm, and h = 25cm.
(a) ∵ Surface area of the herbarium =2 [lb + bh + hl]
= 2 [(30 × 25) + (25 × 25) + (25 × 30)] cm2
= 2 [750 + 625 + 750] cm2
= 2 [2125] cm2 = 4250 cm2
⇒ The surface area of the herbarium = 4250 cm2(b) Total length of 12 edges = 4l + 4b + 4h = 4 [l + b + h]
= 4 [30 + 25 + 25] cm
= 320 cm ⇒ 320 cm of tape is needed.(c) The Mathematical concept used in the above problem is Surface Areas and Volumes [Mensuration]
(d) The skill is depicted by Rahul is Betterment of the environment.
Q3: The Gram Panchayat of a village, plan to construct an underground cuboidal reservoir for water harvesting which is 2 km long, 40 m wide, and 3 m deep.
(a) Find the volume of water which can be stored in the reservoir.
(b) Which mathematical concept is used in the above problem?
(c) Which skill is depicted by the Gram Panchayat by constructing a water reservoir?
Sol:
(a) ∴ Dimensions of the cuboidal reservoir are:
l = 2 km = 2000 m , b = 40 m and h = 3 m
∴ Volume (capacity) of the reservoir = l × b × h = 2000 × 40 × 3 m3 = 240000 m3(b) The mathematical concept is used in the above problem is Mensuration [Surface Areas and Volumes]
(c) The skill is depicted by the Gram Panchayat by constructing a water reservoir is Protection of the natural resources.
Q4: Rahul is having his birthday this coming Sunday. His father is planning to spend ₹ 3850.00 on his birthday. But Rahul has a different idea.
He wishes to serve soup to patients in a hospital. The cost of 1 liter of soup is ₹ 50, it is served in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, then :
(a) How many patients can be served with soup?
(b) Which mathematical concept is used in the above problem?
(c) By spending is birthday money for patients, which values are depicted by Rahul?
Sol:
(a)
= 11 × 7 × 2 cm3 = 154 cm3
Let number of patients served = x
∴ Volume of soup served to x patients = 154 x cm3Cost of 154 x cm3 soup =
⇒
= 3850
⇒
⇒ Number of patients served with soup = 500
(b)The mathematical concept is used in the above problem is Mensuration [Surface Areas and Volumes]
(c) The skill is depicted by the Gram Panchayat by constructing a water reservoir is Serving the patients and Proper use of money.
Q5: Nitin used to save a part of his pocket money. He wishes to buy paint for a community centre from his savings. He buys paint in a certain container which is sufficient to paint an area equal to 9.375 m2.
(a) How many bricks of dimensions 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?
(b) Which mathematical concept is used in the above problem?
(c) By using pocket-money saving to buy paints for community centres, which values are depicted by Nitin?
Sol:
(a) Since, a brick is like a cuboid having l = 22.5 cm, b = 10 cm, h = 7.5 cm
∴ Total surface area of a brick = 2 [lb + bh + hl]
= 2 [(22.5 × 10) + (10 × 7.5) + (7.5 × 22.5)] cm2
= 2 [225 + 75 + 168.75] cm2
= 2 [468.75] cm2 = 937.5 cm2
Let the required number of bricks = n
Thus the required number of bricks = 100
(b) The mathematical concept is used in the above problem is Mensuration [Surface Areas and Volumes]
(c) The skill is depicted by the Gram Panchayat by constructing a water reservoir is Saving money and Charity.
Q6: Sumit helped his friend to pitch a tent on the campsite. The tent is cylindrical in shape with a conical top above it. The radius of the base of the tent is 7m. The height of the cylindrical part is 20 m and the height of the conical part is 4 m.
(a) Find the area of canvas cloth needed to construct the tent.
(b) Which Mathematical concept is used here.
(c) Which skills are depicted by Sumit?
Sol:
(a) Curved surface area of cylindrical part = 2πrh
= 2 × (22/7) × 7 × 20
= 880 m²For finding the surface area of the curved part of the cone, we have to find l, the slant height.
l = √(r² + h²) = √(16 + 49) cm = √65 = 8.06 cm
∴ Surface area of the curved part of the cone = πrl
= (22/7) × 7 × 8.06 m²
= 177.32 m²∴ Total area of canvas needed = (880 + 177.32) m²
= 1057.32 m²
(b) The mathematical concept used here is Surface Area
(c) The skills depicted by Sumit are friendship and tentpitching.
Q7: 35 students of class IX of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard.
(a) How much cardboard was required to be bought for the competition?
(b) Which mathematical concept is used in the above problem?
(c) By making cylindrical penholders and decorating them, which skills are depicted by the students of class IX?
Sol:
(a) Here, the penholders are in the form of cylinders.
Radius of a cylinder (r) = 3 cm
Height of a cylinder (h) = 10.5 cm
Since, each penholder is open from the top
∴ Surface area of a penholder (cylinder) = [Lateral surface area] + [Base area]
⇒ Total surface area of 35 penholders
= 5 × 1584 cm2 = 7920 cm2
Thus, 7920 cm2 of cardboard was required to be bought for 35 competitors.(b) The mathematical concept is used in the above problem is Surface Areas and Volumes
(c) The skill is depicted by the Gram Panchayat by constructing a water reservoir is Healthy competition and creativity.
Q8: Students of class IX of the Sagar School plan to have their school bus stand barricaded from the remaining part of the road to avoid inconveniencing the people. For this purpose, they use 50 hollow cones made of recycled cardboard. Each cone has a diameter of 40 cm and a height 1m.
They painted the outer side of each of the cones. The cost of painting is ₹ 12 per m2.
[use π = 3.14 and √(1.04) = 1.02]
(a) Find the cost of painting of all these cones.
(b) Which mathematical concept is used in the above problem?
(c) By barricading the school-bus stand using cones of recycled cardboard, which skills are depicted by the students of class IX of the Sagar School?
Sol.:
(a) Diameter of a cone = 40 cm
∴ Radius of a cone (r)= 40
2 cm = 20 cm = 20 m 100
= 0.2 m Height of a cone (h)= 1m
⇒ Slant height of a cone (l)=
= 1.02 m [∵ It is given that √(1.04)= 1.02]
Now, curved surface area of a cone = πrl [∵ Base of the cone is hollow]
⇒ Curved surface area of 1 cone = 3.14 × 0.2 × 1.02 m2
⇒ Curved surface area of 50 cones
Cost of Painting :
∵ The rate of painting is ₹ 12 per m2∴ Total cost of 50 cones
(b) The mathematical concept is used in the above problem is Surface Areas and Volumes [mensuration]
(c) The skill is depicted by the Gram Panchayat by constructing a water reservoir is Care for the public convenience and Betterment of the environment.
Q9: Rohit has set up a juice shop. He has two types of packs:
Type A: A cylindrical tin cane with a circular base of diameter 7 cm and height 10 cm.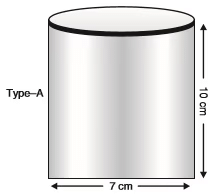 Type B: A rectangular plastic cane with base length 5 cm and width of 4 cm and having height of 15 cm.
Type B: A rectangular plastic cane with base length 5 cm and width of 4 cm and having height of 15 cm.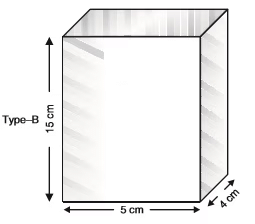
He decided to serve the customers in ‘A’ type of packs.
(a) Find the volume of the pack ‘A’.
(b) Which pack has the greater capacity?
(c) Which mathematical concept is used in above problem?
(d) By choosing a pack of type-A and avoiding a plastic pack, which values are depicted by Rohit?
Sol:
(a) Volume of the cylindrical pack :
∵ Base diameter = 7 cm
∴ Radius (r)= 7
2 cm Height (h) = 10 cm
∵ Volume = πr2h
⇒ = 11 × 7 × 5 cm3 = 385 cm3
⇒ The volume of the cylindrical pack is 385 cm3(b) Volume of rectangular pack : Length
(l) = 5 cm Breadth(b) = 4 cm Height (h) = 15 cm
∴ Volume = lbh = 5 × 4 × 15 cm3 = 300 cm3
Since, 385 cm3 > 300 cm3
⇒ Capacity of cylindrical pack is greater.
(c) The mathematical concept is used in the above problem is Surface Areas and Volumes [mensuration]
(d)The skill is depicted by the Gram Panchayat by constructing a water reservoir is Honesty and Betterment of the environment.
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths Chapter 11 Question Answers - Surface Areas and Volumes
| 1. What are the different formulas for calculating the surface area of common geometric shapes? |  |
| 2. How do you derive the volume formula for a cylinder? |  |
| 3. What is the difference between surface area and volume? |  |
| 4. How can I apply surface area and volume concepts in real-life situations? |  |
| 5. What are some common mistakes to avoid when calculating surface areas and volumes? |  |

















