Ex-1.1 Number System, Class 9, Maths RD Sharma Solutions | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q1. Is 0 a rational number? Can you write it in the form P/Q , where P and Q are integers and Q ≠ 0?
Solution:
Yes, 0 is a rational number and it can be written in P÷Q form provided that Q ≠ 0
0 is an integer and it can be written various forms, for example
0÷2,0÷100,0÷95 etc.
Q2. Find five rational numbers between 1 and 2
Solution:
Given that to find out 5 rational numbers between 1 and 2
- Rational number lying between 1 and 2
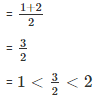
- Rational number lying between 1 and 3/2
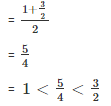
- Rational number lying between 1 and 5/4
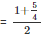 Rational number lying between 3/2 and 2
Rational number lying between 3/2 and 2
= 9/2
= 1 < 9/8 < 5/4 - Rational number lying between 3/2 and 2
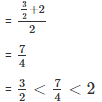
- Rational number lying between 7/4 and 2
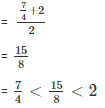
Therefore,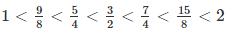
Q3. Find out 6 rational numbers between 3 and 4
Solution:
Given that to find out 6 rational numbers between 3 and 4
We have,
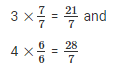
We know 21 < 22 < 23 < 24 < 25 < 26 < 27 < 28
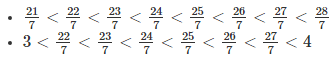
Therefore, 6 rational numbers between 3 and 4 are
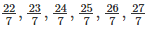
Similarly to find 5 rational numbers between 3 and 4, multiply 3 and 4 respectively with 6/6 and in order to find 8 rational numbers between 3 and 4 multiply 3 and 4 respectively with 8/8 and so on.
Q4. Find 5 rational numbers between 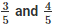
Solution : Given to find out the 5 rational numbers between 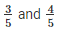
To find 5 rational numbers between 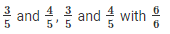
We have,
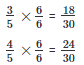
We know 18 < 19 < 20 < 21 < 22 < 23 < 24
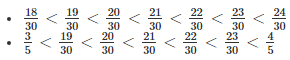
Therefore, 5 rational numbers between 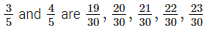
Q5. Answer whether the following statements are true or false? Give reasons in support of your answer.
(i) Every whole number is a rational number
(ii) Every integer is a rational number
(iii) Every rational number is an integer
(iv) Every natural number is a whole number
(v) Every integer is a whole number
(vi) Every rational number is a whole number
Solution:
(i) True. As whole numbers include and they can be represented
For example 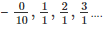 . And so on.
. And so on.
(ii) True. As we know 1, 2, 3, 4 and so on, are integers and they can be represented in the form of 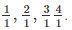
(iii) False. Numbers such as 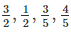 are rational numbers but they are not integers.
are rational numbers but they are not integers.
(iv) True. Whole numbers include all of the natural numbers.
(v) False. As we know whole numbers are a part of integers.
(vi) False. Integers include -1, -2, -3 and so on….. .which is not whole number
FAQs on Ex-1.1 Number System, Class 9, Maths RD Sharma Solutions - RD Sharma Solutions for Class 9 Mathematics
| 1. What is the importance of studying the number system in class 9 mathematics? |  |
| 2. How can I identify whether a given number is rational or irrational? |  |
| 3. How do I convert a recurring decimal into a fraction? |  |
| 4. How do I determine the HCF and LCM of two or more numbers? |  |
| 5. How do I determine the square root of a given number? |  |

















