Class 10 Maths Chapter 12 Previous Year Questions - Surface Area and Volumes
| Table of contents |

|
| Previous Year Questions 2019 |

|
| Previous Year Questions 2018 |

|
| Previous Year Questions 2017 |

|
| Previous Year Questions 2016 |

|
| Previous Year Questions 2015 |

|
Previous Year Questions 2019
Q1: A solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 20 cm and the diameter of the cylinder is 7 cm. Find the total volume of the solid, (use π = 22/7) [Allahabad 2019] View Answer
View AnswerAns: Diameter of cylinder
= diameter of the hemisphere = 7 cm
∴ Radius of cylinder = 7/2 cm
Total height of the solid = 20 cm
Height of the cylinder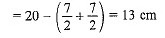
Volume of the solid
= volume of the cylinder + 2 x volume of one hemisphere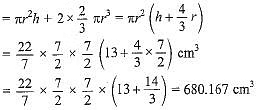
Q2: A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom of circular ends of the bucket are 20 cm and 12 cm respectively. Find the height of the bucket and also the area of the metal sheet used in making it. (Use π = 3.14) [CBSE 2019 (30/1/2)]
 View Answer
View AnswerAns: r = 12 cm, R = 20 cm, V = 12308.8 cm3 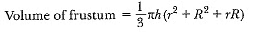
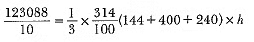
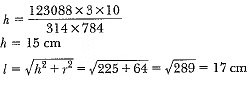
Area of metal sheet used = π(R + r)l + πr2
= π(20 + 12) x 17 + π x 144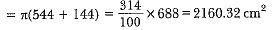
Hence, the height of the bucket is 15 cm and the area of the metal sheet used is 2160.32 cm2.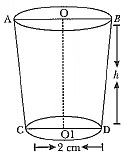
Q3: An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet (Fig. 13.37). The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also, find the volume of water the bucket can hold. 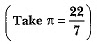 [CBSE 2019(30/5/1)]
[CBSE 2019(30/5/1)]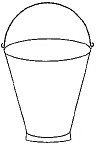
 View Answer
View AnswerAns: The total height of the bucket = 40 cm, which includes the height of the base. So, the height of the frustum of the cone = (40 - 6) cm = 34 cm.
Therefore, the slant height of the frustum,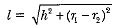
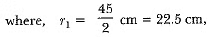
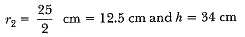
So, 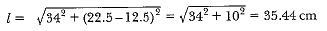
Area of the metallic sheet used
Curved surface area of frustum of cone + Area of circular base + Curved surface area of cylinder
= [π x 35.44 (22.5 + 12.5) + π x (12.5)2 + 2π x 12.5 x 6] cm2 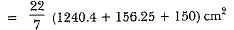
= 4860.9 cm2
Now, the volume of water that the bucket can hold (also, known as the capacity of the bucket)
Q4: A cylindrical bucket, 32 cm high and with a radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
OR
A girl empties a cylindrical bucket, full of sand, of base radius 18 cm and height 32 cm, on the floor to form a conical heap of sand. If the height of this conical heap is 24 cm, then find its slant height correct up to one place of decimal.
[CBSE (E) 2014, 2019 (30/5/1)]
 View Answer
View AnswerAns: We have,
Radius of cylindrical bucket =18 cm
Height of cylindrical bucket = 32 cm
And the height of conical heap = 24 cm
Let the radius of the conical heap be r cm
Volume of the sand = volume of the cylindrical bucket
= πr2h = π x (18)2 x 32
Now, volume of conical heap 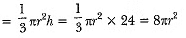
Here, volume of the conical heap will be equal to the volume of sand
∴ 8πr2 = π x (18)2 x 32
⇒ r2 = 18 x 18 x 4 = (18)2 x (2)2
⇒ r2 = (36)2 or r = 36 cm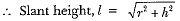
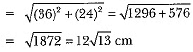
Previous Year Questions 2018
Q5: The diameters of the lower and upper ends of a bucket in the form of a frustum of a cone are 10 cm and 30 cm respectively. If its height is 24 cm, find the area of the metal sheet used to make the bucket. [Use π = 3.14] [CBSE 2018] View Answer
View AnswerAns: For bucket,
Upper diameter (D) = 30 cm
∴ 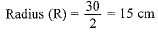
Lower diameter (d) = 10 cm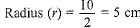
Height of bucket (h) = 24 cm
∴ The area of the metal sheet used = CSA of the frustum (bucket) + Area of bottom part (base)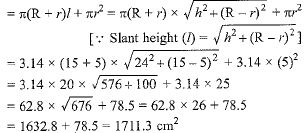
Previous Year Questions 2017
Q6: A metallic right circular cone 20 cm high whose vertical angle is 60° which is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/16 cm, find the length of the wire. [NCERT, CBSE (F) 2017] View Answer
View AnswerAns: Let VAB be the metallic right circular cone of height 20 cm. Suppose this cone is cut by a plane parallel to its base at a point O' such that VO' = O' O i.e., O' is the midpoint of VO.
Let r1 and r2 be the radii of circular ends of the frustum ABB' A'.
Now, in ΔVOA and VO' A', we have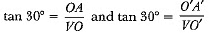
⇒ 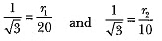
⇒ 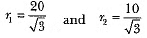
∴ Volume of the frustum = 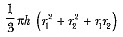
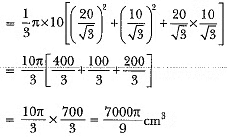
Let the length of wire of diameter 1/16 cm be l cm. Then,
Volume of metal used in wire 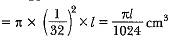
Since the frustum is recast into a wire of length l cm and diameter 1/16 cm.
∴ Volume of the metal used in wire = volume of the frustum
⇒ 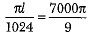
⇒ 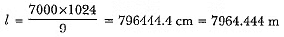
Q7:A solid metallic cylinder of diameter 12 cm and height 15 cm is melted and recast into toys each in the shape of a cone of radius 3 cm and height 9 cm. Find the number of toys so formed. [AI 2017 (C)]
 View Answer
View AnswerAns: Diameter of metallic cylinder = 12 cm
∴ Radius of metallic cylinder (r) = 6 cm
Height (h) = 15 cm
Volume of cylinder = πr2h = π(6)2 x 15 cm3
Radius of cone = 3 cm
Height of cone = 9 cm
Volume of cone = 1/3 π(3)2 x 9 = 3 x 9π cm3
Number of toys so formed = 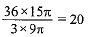
If the question is “A tent is in the form of a cylinder surmounted by a cone. Find the capacity of the tent and the cost of canvas for making the tent at Rs 100 per sq.m.”, then the solution is given as “Tent is a combination of a cylinder and a cone. For capacity
∴ Volume (capacity) of the tent = Volume of the cylindrical part + Volume of the conical part
For the cost of the canvas, we find the total surface area.
Total surface area = Curved area of the cylindrical part + Curved surface area of the conical part
Now, proceed to find its cost.”
Note: Don’t solve as “Total surface area of canvas = Total surface area of cylinder + Total surface area of a cone and proceed further"
This is the wrong solution.
Q8: The 3/4th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with an internal radius of 10 cm. Find the height of water in a cylindrical vessel. [Delhi 2017]
 View Answer
View AnswerAns: Radius of conical vessel (r) = 5 cm
Height of conical vessel (h) = 24 cm
Radius of cylindrical vessel (R) = 10 cm
Let H be the height of water in the cylindrical vessel Now, the total volume of the conical vessel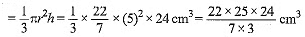
According to the question,
3/4 of the volume of water from the conical vessel is emptied into the cylindrical vessel.
⇒ 3/4 x Volume of conical vessel =Volume of water in the cylindrical vessel.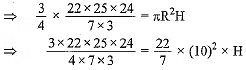
⇒ 25 x 6 = 10 x 10 x H
⇒ 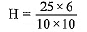
⇒ H = 1.5 cm
∴ Height of water in the cylindrical vessel = 1.5 cm
Q9: In a rain-water harvesting system, the rainwater from a roof of 22 m x 20 m drains into a cylindrical tank having a diameter of base 2 m and height of 3.5 m. If the tank is full, find the rainfall in cm. [AI 2017]
 View Answer
View AnswerAns: Length of roof (l) = 22 m
Breadth of roof (b) = 20 m
Let the height of water column collected on roof= hm
∴ Volume of standing water on rooftop = lbh
= (22 x 20 x h) m3
This water is taken into a cylindrical tank of diameter of base 2 m and height 3.5 m.
Tank gets completely filled with this amount of water.
⇒ Volume of water from roof-top = Volume of cylinder
Diameter of tank = 2 m
∴ Radius of tank = 2/2 = 1 m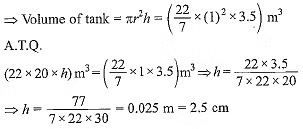
Hence rainfall is 2.5 cm.
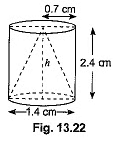
Q10: From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2. [CBSE (AI) 2017]
 View Answer
View AnswerAns: We have,
Radius of the cylinder = 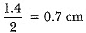 Height of the cylinder = 2.4 cm
Height of the cylinder = 2.4 cm
Also, radius of the cone = 0.7 cm and height of the cone = 2.4 cm
Now, slant height of the cone =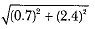
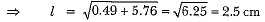
∴ Total surface area of the remaining solid
= curved surface area of cylinder + curved surface area of the cone + area of upper circular base of the cylinder.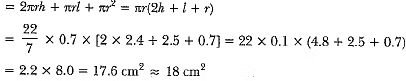
Previous Year Questions 2016
Q11: A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by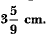 Find the diameter of the cylindrical vessel. [CBSE (AI) 2016]
Find the diameter of the cylindrical vessel. [CBSE (AI) 2016] View Answer
View AnswerAns: Volume of sphere = 4/3 π(6)3 cm3
Volume of water rise in cylinder = 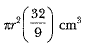
∴ 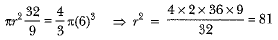
⇒ r = 9 cm
Previous Year Questions 2015
Q12: Two spheres of the same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere. [CBSE (F) 2015] View Answer
View AnswerAns: Volume of the smaller sphere 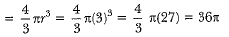
Volume of smaller sphere x density = mass
∴ 36π (density of metal) = 1
Density of metal = 1/36π
∴ Volume of bigger sphere x density = mass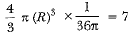
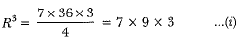
Volume of new sphere = volume of smaller sphere + volume of bigger sphere
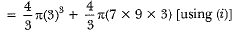
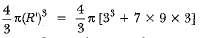
(R')3 = [33 + 7 x 33]
(R')3 = 33(l + 7)
(R')3 = 33 x 8
(R')3 = 33 x 23
R' =3 x 2
R' = 6 cm
∴ Diameter of new sphere =12 cm.
Q13: A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer. [CBSE (AI) 2015]
 View Answer
View AnswerAns: Radius of hemispherical bowl, R = 36/2 = 18 cm
Radius of cylindrical bottle, r = 6/2 = 3 cm
Let height of cylindrical bottle = h
Since 10% liquid is wasted, therefore only 90% liquid is filled into 72 cylindrical bottles.
∴ The volume of 72 cylindrical bottles = 90% of the volume in the bowl
⇒ 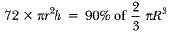
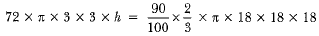
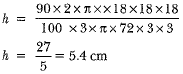
Q14: In Fig. a cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts. [CBSE (AI) 2015]
 View Answer
View AnswerAns: Let.BC = r cm, DE = 10 cm
Since B is the mid-point of AD and BC is parallel to DE, therefore C is the mid-point of AE.
∴ AC = CE
Also, ΔABC ~ ΔADE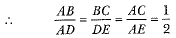
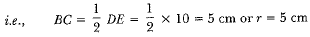
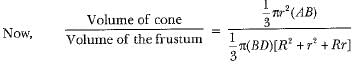
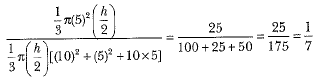
∴ The required ratio = 1 : 7.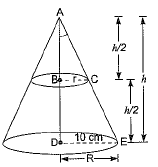
|
122 videos|116 docs|74 tests
|
FAQs on Class 10 Maths Chapter 12 Previous Year Questions - Surface Area and Volumes
| 1. How do you calculate the surface area of a cylinder? |  |
| 2. What is the difference between surface area and volume? |  |
| 3. How do you find the surface area of a cone? |  |
| 4. Is there a formula to calculate the volume of a sphere? |  |
| 5. How can surface area and volume calculations be applied in real-life situations? |  |





















