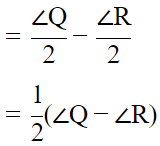NCERT Exemplar Solutions: Lines & Angles | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Exercise 6.1 |

|
| Exercise 6.2 |

|
| Exercise 6.3 |

|
| Exercise 6.4 |

|
Exercise 6.1
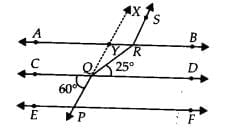
Q.1. In Fig. 6.1, if AB || CD || EF, PQ || RS, ∠RQD = 25° and ∠CQP = 60°, then ∠QRS is equal to
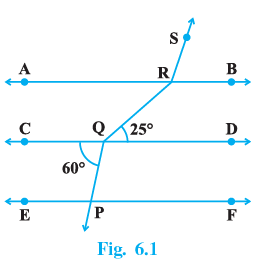
(a) 85°
(b) 135°
(c) 145°
(d) 110°
Correct Answer is Option (c)
Produced PQ to X which intersect AB at Y.
PQ || RS ⇒ PX || RS∵ AB || CD and PX is transversal
∠CQP + ∠AYX = 180° [Co-exterior angles]
⇒ 60° + ∠AYX = 180°
⇒ ∠AYX = 180° – 60°
⇒ ∠AYX = 120°
∵ PX || RS and AB is transversal
∠YRS = ∠AYX [Corresponding angles]
⇒ ∠YRS = 120° …(i)
and AB || CD and RQ is transversal
∠YRQ = ∠RQD [Alternate interior angles]
⇒ ∠YRQ = 25° …(ii)
Now, ∠SRQ = ∠SRY + ∠YRQ
⇒ ∠SRQ = 120° + 25° [From (i) and (ii)]
⇒ ∠SRQ = 145°
Q.2. If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
(a) an isosceles triangle
(b) an obtuse triangle
(c) an equilateral triangle
(d) a right triangle
Correct Answer is Option (d)
Let the angles of a triabgle be α,β,γ
Given α + β = γ
We now that in a sum of triangles sum of angles is 180°
So, α + β + γ = 180°
⇒ 2γ = 180°⇒ γ = 90 °
So, it is a right angled triangle.
Q.3. An exterior angle of a triangle is 105° and its two interior opposite angles are equal. Each of these equal angles is
(a) 37(1/2)°
(b) 52(1/2)°
(c) 72(1/2)°
(d) 75°
Correct Answer is Option (b)
Let one of the interior opposite angle of a triangle be x.
∵ Exterior angle
= sum of two opposite interior angles
∴ x + x = 105° [ ∵ Exterior angle = 105° and two interior opposite angles are equal]
⇒ 2x = 105° ⇒ x = 52(1/2)°.
Thus, each of the required angles of a triangle 52(1/2)°.
Q.4. The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is
(a) an acute angled triangle
(b) an obtuse angled triangle
(c) a right triangle
(d) an isosceles triangle
Correct Answer is Option (a)
We have given, the ratio of angles of a triangle is 5 : 3 : 7.
Let angles of a triangle be ∠A, ∠B and ∠C, where ∠A = 5x, ∠B = 3x and ∠C = 7x
Now in ∆ABC, ∠A + ∠B + ∠C = 180° [Angle sum property of a triangle]
∴ 5x + 3x + 7x = 180°
⇒ 15x = 180°
So, ∠A = 5 × 12° = 60°, ∠B = 3 × 12° = 36° and ∠C = 7 × 12° = 84°
∵ All angles are less than 90°, hence the triangle is an acute angled triangle.
Q.5. If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be
(a) 50°
(b) 65°
(c) 145°
(d) 155°
Correct Answer is Option (d)
Consider a △ABC,such that ∠BAC=130° and bisectors of ∠B and ∠C meet at O.
To find: ∠BOC
Now, in △ABC,
∠BAC + ∠ABC + ∠ACB = 180°
130° + ∠ABC+∠ACB = 180° (Angle sum property of a triangle)
∠ABC +∠ACB = 50°
(1/2)(∠ABC + ∠ACB) = 25°
∠OBC + ∠OCB = 25° (OB and OC bisect ∠ABC and ∠ACB respectively)
Now, in △OBC,
∠OBC + ∠OCB + ∠BOC = 180°
25° + ∠BOC = 180°
∠BOC = 155°.
Q.6. In Fig. 6.2, POQ is a line. The value of x is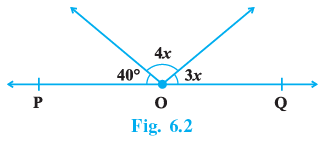
(a) 20°
(b) 25°
(c) 30°
(d) 35°
Correct Answer is Option (a)
Given POQ is a line, POQ = 180°
40° + 4x + 3x = 180°
⇒ 7x = 140°
⇒ x = 20°
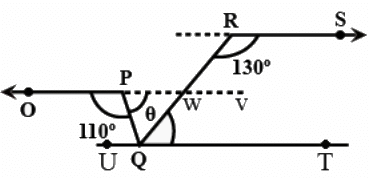
Q.7. In Fig. 6.3, if OP||RS, ∠OPQ = 110° and ∠QRS = 130°, then ∠ PQR is equal to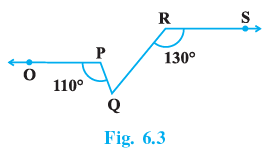
(a) 40°
(b) 50°
(c) 60°
(d) 70°
Correct Answer is Option (c)
Using the fact that OP || RS, we know that
∠RWV = 180° − 130°
1. ∠RWV = 50°
We know that,
∠PWQ = ∠RWV = 50° (Since, opposite angles of intersecting lines are equal)
Also, for line OP
∠OQP + θ = 180°
θ = 180° − ∠OPQ = 180° − 110°
2. θ = 70°
Now, we know that sum of angles of a triangle is 180°,
∠PQR + θ + ∠PWQ = 180°
∠PQR = 180° − θ − ∠PWQ = 180° − 70° − 50°
∠PQR = 180° − 120°
∠PQR = 60°
Q.8. Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is
(a) 60°
(b) 40°
(c) 80°
(d) 20°
Correct Answer is Option (b)
The angles of the triangle are in the ratio: 2 : 4 : 3
Let the angles be 2x, 4x, 3x
By Angle sum property,
2x + 4x + 3x = 180°
9x = 180°
x = 20°
Thus, angles are, 40°, 80° , 60°
Thus, the smallest angle = 40°
Exercise 6.2
Q.1. For what value of x + y in Fig. 6.4 will ABC be a line? Justify your answer.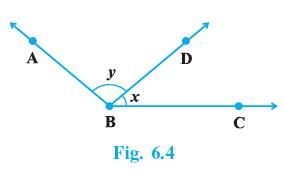
The value of x + y can't be find out with the given data.
No, ABC is not a line as it not straight, it is bent at point B.
Q.2. Can a triangle have all angles less than 60°? Give reason for your answer.
By angle sum property, we know, the sum of all angles of a triangle = 180°.
⇒ 60° + 60° + 60°
= 180°.
If all the these angles is less than 60°, then there sum together would not make 180°.
Say for example, 30°, 40° and 50° are 3 angles of the triangle.
∴ 30 + 40 + 50 = 120° < 180° .
Therefore, it is not possible.
Hence, the answer is No.
Q.3. Can a triangle have two obtuse angles? Give reason for your answer.
An angle whose measure is more than 90° but less than 180° is called an obtuse angle.
An triangle cannot have two obtuse angles because the sum of all the angles of it cannot be more than 180°. It is always equal to 180°.
Q.4. How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
The three angles given are 45°, 64°, 72°
Now, sum of angles = 45 + 64 +72
Sum of angles = 181°
Sum of angles of triangle cannot be more than 180°.
Hence, triangle is not possible.
Q.5. How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
The three angles given are 53°, 64°, 63°
Now, sum of angles = 53° + 64° + 63°
Sum of angles = 180°
Sum of angles of triangle is 180°.
Hence, infinitely many triangles can be formed with these three angles.
Q.6. In Fig. 6.5, find the value of x for which the lines l and m are parallel.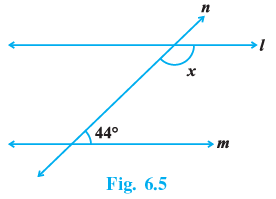
Given, l ∥ m
∠x and 44° are co interior angles. Sum of the co - interior angles is 180° .
Hence, ∠x + 44 = 180
∠x = 136°
Q.7. Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
No it is not necessary.
Two angles are said to be adjacent when they have common vertex, a common side but do not overlap. They can be of any measure. For example, 33° and 25° can be two adjacent angles.
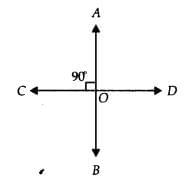
Q.8. If one of the angles formed by two intersecting lines is a right angle, what can you say about the other three angles? Give reason for your answer.
Let AB and CD be two lines intersecting at O, such that, ∠AOD = 90°
Now, ∠AOD = ∠COB = 90° (Vertically opposite angles)
⇒ ∠AOD + ∠DOB = 180° (Angles on a straight line)
⇒ 90 + ∠DOB = 180°
∠DOB = 90°
∠DOB = ∠AOC = 90° (Vertically opposite angles)
Thus, all angles are 90°.
Q.9. In Fig.6.6, which of the two lines are parallel and why?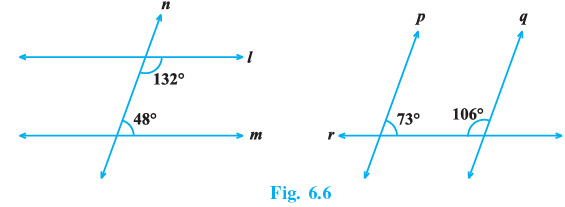
For fig(i) , a transversal intersects two lines such that the sum of interior angles on the same side on the same side of the transversal is 132° +48° = 180°.
Therefore , the line l and m are parallel.
For fig.(ii) , a transversal intersects two lines such that the sum of interior angles on the same side of the transversal is 73° +106° = 179°.
Therefore , the lines p and q are not parallel.
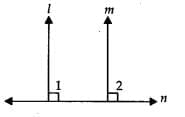
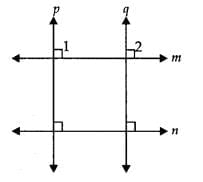
Q.10. Two lines l and m are perpendicular to the same line n. Are l and m perpendicular to each other? Give reason for your answer.
No
Given that the lines l and m are perpendicular to the line n.
∴ ∠1 = ∠2 = 90°
This shows that the corresponding angles are equal.
Thus, l || m.
Exercise 6.3
Q.1. In Fig. 6.9, OD is the bisector of ∠AOC, OE is the bisector of ∠BOC and OD ⊥ OE. Show that the points A, O and B are collinear.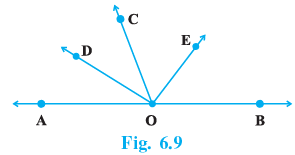
Since, OD and OE bisects ∠AOC and ∠BOC, respectively.
∴ ∠AOC = 2∠DOC …(i)
and ∠COB = 2 ∠COE …(ii)
On adding (i) and (ii), we get
∠AOC + ∠COB = 2 ∠DOC + 2 ∠COE
⇒ ∠AOC + ∠COB = 2 (∠DOC + ∠COE)
⇒ ∠AOC + ∠COB = 2 ∠DOE
⇒ ∠AOC + ∠COB = 2 × 90° [∵ OD ⊥ OE]
⇒ ∠AOC + ∠COB = 180°
As, adjacent angles ∠AOC and ∠COB form a linear pair.
∴ AOB is a straight line.
Thus, points A, O and B are collinear.
Q.2. In Fig. 6.10, ∠1 = 60° and ∠6 = 120°. Show that the lines m and n are parallel.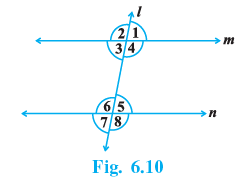
We have ∠1 = 60° and ∠6 = 120°
Now,
∠5 + ∠6 = 180° [linear pair Angles]
⇒ ∠5 + 120° = 180° ⇒ ∠5 = 180° −120° = 60°
Now, ∠1 = ∠5 [Each = 60°]
But, these are corresponding angles.
Therefore, the lines m and n are parallel.
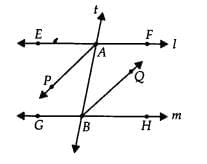
Q.3. AP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (Fig. 6.11). Show that AP || BQ.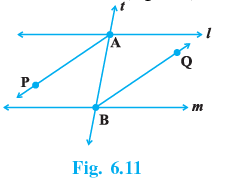
Since, l || m and t is a transversal line.
∴ ∠EAB = ∠ABH [Alternate interior angles]⇒ ∠PAB = ∠ABQ
[∵ AP and BQ are the bisectors of ∠EAB and ∠ABH] Since, ∠PAB and ∠ABQ are alternate interior angles formed by lines AP and BQ and transversal AB. Thus, AP || BQ.
Q.4. If in Fig. 6.11, bisectors AP and BQ of the alternate interior angles are parallel, then show that l || m.
Since, AP || BQ and t is a transversal, therefore, ∠PAB = ∠ABQ
[Alternate interior angles]
⇒ 2 ∠PAB = 2 ∠ABQ
[On multiplying both sides by 2]
⇒ ∠CAB = ∠ABF [ ∵ AP and BQ are the bisectors of ∠CAB and ∠ABF]
Since, ∠CAB and ∠ABF are alternate interior angles formed by lines l and m and transversal t. Thus, l || m.
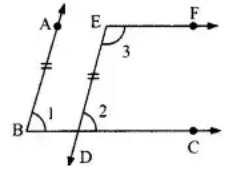
Q.5. In Fig. 6.12, BA || ED and BC || EF. Show that ∠ABC = ∠DEF [Hint: Produce DE to intersect BC at P (say)].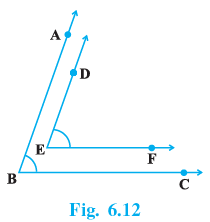
Since BA || ED ⇒ BA || DP
∴ ∠ABP = ∠EPC [Corresponding angles]
or ∠ABC = ∠EPC …(i)
Again, BC || EF or PC || EF
∴ ∠DEF = ∠EPC …(ii)
[Corresponding angles] From (i) and (ii), we get
∠ABC = ∠DEF
Q.6. In Fig. 6.13, BA || ED and BC || EF. Show that ∠ ABC + ∠ DEF = 180°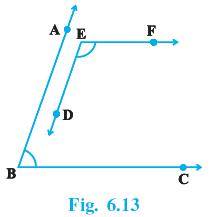
∵ BA ∣∣ ED
∠1=∠2.......(i)
(Corresponding angles)
Also BC || EF
⇒ ∠2 + ∠3 = 180°...(ii)
(Sum of the interior angles on the same side of a transversal is 180°)
From (i) and (ii), we get
∠1 + ∠3 = 180°
i.e. ∠ABC + ∠DEF = 180°
Q.7. In Fig. 6.14, DE || QR and AP and BP are bisectors of ∠ EAB and ∠ RBA, respectively. Find ∠APB.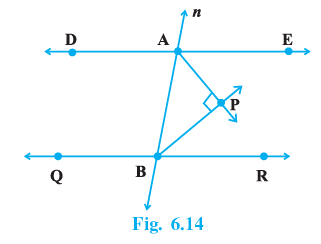
Given: DE∥QR, AP bisects ∠EAB, BP bisects ∠RBA
Since, DE∥QR
∠EAB+∠RBA = 180°
(1/2)(∠EAB+∠RBA) = 90°
∠PAB+∠PBA=90° (AP bisects ∠EAB, BP bisects ∠RBA)
Now, In △PAB
∠PAB + ∠PBA + ∠APB = 180° ( Angle sum property of triangle)
90° +∠APB = 180°
∠APB = 90°
Q.8. The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
Angle sum property of a triangle is 180°. It is given that the angles are in the ratio 2:3:4.
So let us consider the angles as 2x, 3x and 4x.
2x + 3x + 4x = 9x
Angle sum of triangle is 180°
so 9x = 180°
or x = 180/9 = 20°
∴ 2x = 2 × 20°= 40°
3x = 3 × 20° = 60°
and 4x = 4 × 20° = 80°
∴ the angles are 40°, 60°, 80°.
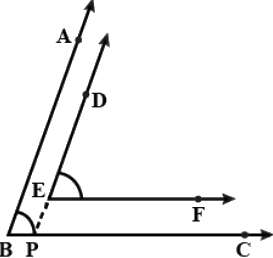
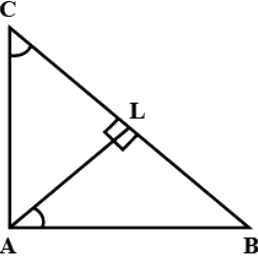
Q.9. A triangle ABC is right angled at A. L is a point on BC such that AL ⊥ BC. Prove that ∠ BAL = ∠ ACB.
Since Δ ABC is right-angled,
AB2 + AC2 = BC2
or, AB2 + AC2 = (BL+ CL)2
or, AB2 +AC2 = BL2 + CL2 + 2.BL.CL ...(1).
Again from Δ ALC and Δ ALB we have
AC2 = AL2 + CL2...(2)
AB2 = AL2 + BL2 ...(3).
Adding (2) and (3) we get,
AC2 + AB2 = 2. AL2 + CL2 + BL2
or, BL2 + CL2 + 2.BL.CL = 2.AL2 + BL2 + CL2or, AL2 = BL.CL ...(4).
Now tan ∠ACB = AL/CL ....(5) and tan ∠ABL = AL/BL
⇒ tan(90° − ∠BAL) = (AL/BL)
⇒ cot ∠BAL = (AL/BL) ...(6)
From (4) we have (AL/CL) = (BL/AL)
or, tan ∠ACB = tan ∠BAL [Using (5) and (6)]
or, ∠ACB = ∠BAL.
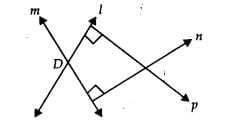
Q.10. Two lines are respectively perpendicular to two parallel lines. Show that they are parallel to each other.
According to the figure consider the two parallel lines m and n
we know that p ⊥ m and q ⊥ n
so we get
∠1 = ∠2 = 90°
We know that m ∥ n and p is a transversal
from the figure, we know that ∠1 and ∠3 are corresponding angles
so we get
∠1 = ∠3
We also know that
∠2 + ∠3 = 90°
We know that ∠2 and ∠3 are corresponding angles when the transversal n cuts p and q
so we get p ∥ q
therefore, it is shown that the two lines which are perpendicular to two parallel lines are parallel to each other.
Exercise 6.4
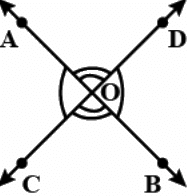
Q.1. If two lines intersect, prove that the vertically opposite angles are equal.
If two lines i.e. AB & CD intersect each other. They have two pair of opp. angles.
i.e.
∠AOC, ∠DOB, ∠AOB, ∠COB.
To prove :- ∠AOC = ∠DOB & ∠AOD = ∠COB
Proof :-
∠AOC + ∠AOD = 180° [linear pair] ___(1)
∠AOD+∠BOD=180° [linear pair] ___(2)
from eq. (1) & (2)
∠AOC + ∠AOD = ∠AOD + ∠BOD
i.e. [∠AOC = ∠BOD]
Similarly [∠AOD = ∠COB] Hence proved.
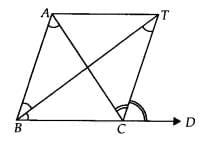
Q.2. Bisectors of interior ∠B and exterior ∠ACD of a ∆ ABC intersect at the point T. Prove that ∠BTC = (1/2)∠BAC.
According to the problem ∠TBC = (1/2)∠B ...(1) and
∠TCD = (1/2) ∠ACD ...(2).
Now from Δ ABC we have
∠A + ∠B = ∠ACD ...(3).
And from ΔTBC we have
∠T + ∠TBC = ∠TCD
or, ∠T + (1/2) ∠B = (1/2) ∠ACD[Using (1) and (2)]
or, ∠T = (1/2) (∠ACD − ∠B)
or, ∠T = (1/2)∠A. [ Using (3)]
or, ∠BTC = (1/2) ∠BAC.
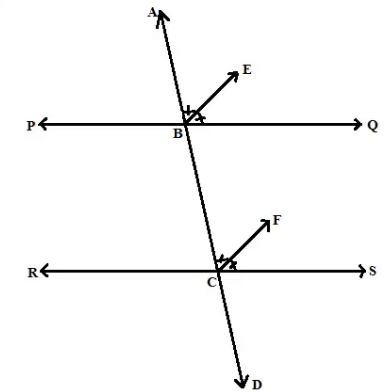
Q.3. A transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel.
The transversal AD intersects the two lines PQ and RS at points B and C respectively. BE is the bisector of ∠ABQ and CF is the bisector of ∠BCS.
As, BE is the bisector of ∠ABQ, then,
∠ABE = (1/2)∠ABQ
In the same way,
∠BCF = (1/2)∠BCS
Since BE and CF are parallel and AD is the transversal, therefore, by corresponding angle axiom,
∠ABE = ∠BCF
(1/2) ∠ABQ = (1/2)∠BCS
∠ABQ = ∠BCS
Therefore, by the converse of corresponding angle axiom, BE ∥ CF.
Q.4. Prove that through a given point, we can draw only one perpendicular to a given line. [Hint: Use proof by contradiction].
From the point P , a perpendicular PM is drawn to the given line AB.
∴ ∠PMB = 90°
Let if possible , we can draw another perpendicular PN to the line AB. Then ,
∠PMB = 90°
∴ ∠PMB = ∠PNB , which is possible only when PM and PN coincide with each other.
Hence , through a given point , we can draw only one perpendicular to a given line.
Q.5. Prove that two lines that are respectively perpendicular to two intersecting lines intersect each other. [Hint: Use proof by contradiction].
If n and p are any two intersecting lines.
Draw two lines such that l ⊥ n and m ⊥ p
To prove: Lines l andm will intersect.
Proof:
Let n and p be two intersecting lines.
Let us assume that l and m do not intersect each other.
Now l ⊥ n (Given)
Let us assume that l ⊥ m
Therefore, m ⊥ n ...(1)
But given that m ⊥ p ...(2)
From (1) and (2), we get n ∥ p
But given, lines n and p intersect each other.
Hence, our assumption is wrong.
Therefore l and m intersect each other.
Q.6. Prove that a triangle must have atleast two acute angles.
Consider a triangle ABC
We have to prove that a triangle must have atleast two acute angles.
By angle sum property,
∠A + ∠B + ∠C = 180°___(1)
Case (1): consider ∠B = 90° and ∠C = 90°
From (1),
∠A + 90° + 90° = 180°
∠A + 180° = 180°
∠A = 180° - 180°
∠A = 0°
Therefore, no triangle can be formed.
Case (2): when two angles are obtuse
Consider ∠B and ∠C are greater than 90°
Let ∠B = 100° and ∠C = 95°
From (1),
∠A + 100° + 95° = 180°
∠A + 195° = 180°
∠A = 180° - 195°
∠A = - 15°
Angle A is negative, which is not possible.
Therefore, no triangle can be formed.
Case (3) : when one angle is 90 and other angle is obtuse
Let ∠B = 90° and ∠C = 100°
From (1),
∠A + 90° + 100° = 180°
∠A + 190° = 180°
∠A = 180° - 190°
∠A = -10°
Angle A is negative, which is not possible.
Therefore, no triangle can be formed.
Case (4) : when two angles are acute
Consider ∠B and ∠C are less than 90
Let ∠B = 80° and ∠C = 60°
∠A + 80° + 60° = 180°
∠A + 140° = 180°
∠A = 180° - 140°
∠A = 40°
Verification:
∠A + ∠B + ∠C = 180°
LHS : 40° + 80° + 60°
= 100° + 80°
= 180°
= RHS
Therefore, triangles can be formed.
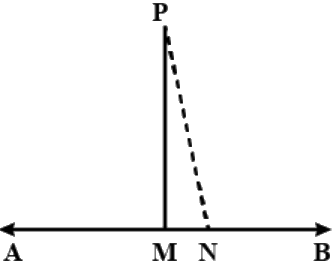
Q.7. In Fig. 6.17, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that∠APM = (1/2) (∠Q – ∠R).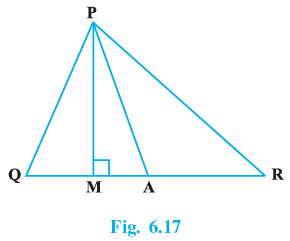
In △PAQ
Sum of two opposite interior angles = Exterior angle
α = θ + ∠θ −(i)
In △PAR
α + θ +∠R = 180°
α = 180° − θ − ∠R −(ii)
In △PMQ
∠MPQ = 180 − ∠Q − 90°
= 90 − ∠Q
∠APM = ∠APQ − ∠MPQ
= θ − (90 − ∠Q)
= θ + ∠Q − 90° −(iii)
∵ (i) = (ii)
⇒ θ + ∠Q = 180° − θ − ∠R
⇒ 2θ = 180° − ∠Q − ∠R
⇒ θ = 90°− (1/2) (∠Q + ∠R)
putting this value of θ in (iii)
∠APM = ∠Q + 90 − (1/2) (∠Q + ∠R) − 90°
∴ a = 2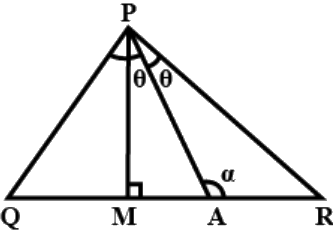
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Exemplar Solutions: Lines & Angles - Mathematics (Maths) Class 9
| 1. What is the angle bisector theorem? |  |
| 2. How do you prove that two angles are complementary? |  |
| 3. What are the properties of perpendicular lines? |  |
| 4. How can you identify if two angles are supplementary? |  |
| 5. What is the significance of collinear points in geometry? |  |