Class 9 Maths Chapter 8 HOTS Questions - Quadrilaterals
Q1: Find all the angles of a parallelogram if one angle is 80°.
Sol:
For a parallelogram ABCD, opposite angles are equal.So, the angles opposite to the given 80° angle will also be 80°.
We also know that the sum of angles of any quadrilateral = 360°.
So, if ∠A = ∠C = 80° then,
∠A + ∠B + ∠C + ∠D = 360°
Also, ∠B = ∠D
Thus,
80° + ∠B + 80° + ∠D = 360°
Or, ∠B +∠ D = 200°
Hence, ∠B = ∠D = 100°
Now, all angles of the quadrilateral are found which are:
∠A = 80°
∠B = 100°
∠C = 80°
∠D = 100°
Q2: In the adjoining figure, ABCD is a parallelogram. Find the angles A, B, C, and D.
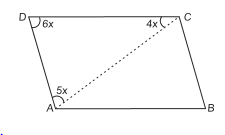
Sol:In ∆ACD, 4x + 5x + 6x = 180°
⇒ 15x = 180°
⇒ x = (180o/15) = 12°
∴ ∠D = 6 × 12° = 72°
⇒ B = 72° [∵ opposite angles of ||gm are equal]
∵ ∠ A + ∠ D = 180° [co-interior angles]
∴ ∠A = 180° – ∠D = 180° – 72° = 180°
⇒ Therefore, ∠ C = 108°
Q3: The sides AD and BC of a quadrilateral are produced as shown in the given figure. Prove that x = ((a+b)/2).
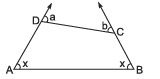
Sol:We have ∠a + ∠ADC = 180° [linear pair]
Similarly, ∠b + ∠BCD = 180°
Adding (a + b) + ∠ADC + ∠BCD = 360° ...(1)
But x + x + ∠ADC + ∠BCD = 360° ...(2)
From (1) and (2)
x + x + ∠ADC + ∠BCD = a + b + ∠ADC + ∠BCD
⇒ x + x = a + b
⇒ 2x = a + b
⇒ x = ((a+b)/2). Hence proved.
Q4: L, M, N, K are midpoints of sides BC, CD, DA and AB respectively of a square ABCD.
Prove that DL, DK, BM and BN enclose a rhombus.
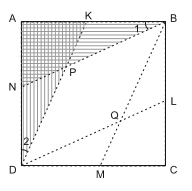
Sol:BK = DM [halves of equal sides]
∴ BM || DK. Similarly, BN || DL
Also, ∆ ABN ≌ ∆ ADK [SAS congruency]
⇒ ∠ 1 = ∠ 2
Also, ∆PND ≌ ∆PKB [ASA congruency]
⇒ PB = PD
⇒ Therefore, DQBP is a rhombus.
Q5: PQRS is a parallelogram. PS is produced to M so that SM = SR and MR produced meet PQ produced at N. Prove that QN = QR.
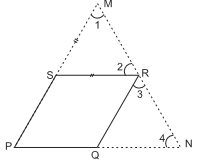
Sol:In ∆SMR, SM = SR
⇒ ∠ 1 = ∠ 2 [Angles opposite to equal sides are equal]
∠1 = ∠3
[∵QR || PM, corresponding angles are equal]
Similarly, ∠2 = ∠4 [corresponding angles]
⇒ ∠ 3 = ∠ 4
⇒ Hence in ∆ QRN, QN = QR
Q6: Calculate all the angles of a quadrilateral if they are in the ratio 2:5:4:1.
Sol:As the angles are in the ratio 2:5:4:1, they can be written as: 2x, 5x, 4x, and x.
Now, as the sum of the angles of a quadrilateral is 360°,
2x + 5x + 4x + x = 360°
Or, x = 30°
Now, all the angles will be,
2x =2 × 30° = 60°
5x = 5 × 30° = 150°
4x = 4 × 30° = 120°, and
x = 30°
Q7: Calculate all the angles of a parallelogram if one of its angles is twice its adjacent angle.
Sol:
Let the angle of the parallelogram given in the question statement be “x”.Now, its adjacent angle will be 2x.
It is known that the opposite angles of a parallelogram are equal.
So, all the angles of a parallelogram will be x, 2x, x, and 2x
As the sum of interior angles of a parallelogram = 360°,
x + 2x + x + 2x = 360°
Or, x = 60°
Thus, all the angles will be 60°, 120°, 60°, and 120°.
Q8: In a trapezium ABCD, AB∥CD. Calculate ∠C and ∠D if ∠A = 55° and ∠B = 70°.
Sol:
In a trapezium ABCD, ∠A + ∠D = 180° and ∠B + ∠C = 180°So, 55° + ∠D = 180°
Or, ∠D = 125°
Similarly,
70° + ∠C = 180°
Or, ∠C = 110°
Q9: In a rectangle, one diagonal is inclined to one of its sides at 25°. Measure the acute angle between the two diagonals.
Sol:
Let ABCD be a rectangle where AC and BD are the two diagonals which are intersecting at point O.Now, assume ∠BDC = 25° (given)
Now, ∠BDA = 90° – 25° = 65°
Also, ∠DAC = ∠BDA, (as diagonals of a rectangle divide the rectangle into two congruent right triangles)
So, ∠BOA = the acute angle between the two diagonals = 180° – 65° – 65° = 50°
Q10: If the bisectors of the angles of a quadrilateral enclose a rectangle, then show that it is a parallelogram.
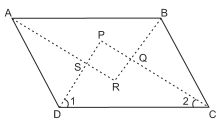
Sol:
Angle bisectors of the quadrilateral ABCD enclose a rectangle PQRS.
∴ ∠P = 90o
⇒ In Δ PCD, ∠1+∠2 = 90o
But, ∠1 and ∠2 are 1/2∠D and 1/2 ∠C respectively.
⇒ ∠D +∠C = 180o [∵ 2∠1 + 2∠2 = 180o]
⇒ ∠ D and ∠ C form a pair of co-interior supplementary angles AD || BC
Similarly, AB || DC ⇒ ABCD is a parallelogram.
|
40 videos|470 docs|56 tests
|
FAQs on Class 9 Maths Chapter 8 HOTS Questions - Quadrilaterals
| 1. What are the properties of a quadrilateral? |  |
| 2. How do you find the area of a quadrilateral? |  |
| 3. What is the difference between a square and a rectangle? |  |
| 4. How do you classify quadrilaterals? |  |
| 5. Can a quadrilateral have more than one type of symmetry? |  |

















