Chapter 20 - Mensuration - I (Part - 1), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 20.13:
Question 1:
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m²?
ANSWER:
Given:Base of a flooring tile that is in the shape of a parallelogram = b = 24 cm
Corresponding height = h = 10 cm
Now,in a parallelogram:Area(A) = Base (b) × Height (h)
∴ Area of a tile = 24 cm × 10 cm = 240 cm²
Now, observe that the area of the floor is 1080 m².1080 m²
= 1080 × 1m × 1m
= 1080 × 100 cm × 100 cm ( Because 1 m = 100 cm)
= 1080 × 100 × 100 × cm × cm
= 10800000 cm²
∴ Number of required tiles = 10800000/240 = 45000
Hence, we need 45000 tiles to cover the floor.
Question 2:
A plot is in the form of a rectangle ABCD having semi-circle on BC as shown in Fig. 20.23. If AB = 60 m and BC = 28 m, find the area of the plot.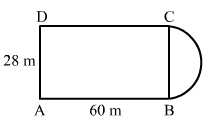
ANSWER:
The given figure has a rectangle with a semicircle on one of its sides. The given figure has a rectangle with a semicircle on one of its sides. 
Total area of the plot = Area of rectangle ABCD + Area of semicircle with radius (r = 28/2 = 14m)
∴ Area of the rectangular plot with sides 60m and 28m = 60 × 28 = 1680 m² ...(i)
And, area of the semicircle with radius 14m = 1/2π × (14)2 = 1/2 × 22/7 × 14 × 14 = 308m² ...(ii)
∴ Total area of the plot = 1680 + 308 = 1988m² ...(from (i) and (ii))
Question 3:
A playground has the shape of a rectangle, with two semi-circles on its smaller sides as diameters, added to its outside. If the sides of the rectangle are 36 m and 24.5 m, find the area of the playground. (Take π = 22/7).
ANSWER:
It is given that the playground is in the shape of a rectangle with two semicircles on its smaller sides. Length of the rectangular portion is 36 m and its width is 24.5 m as shown in the figure below.It is given that the playground is in the shape of a rectangle with two semicircles on its smaller sides. Length of the rectangular portion is 36 m and its width is 24.5 m as shown in the figure below.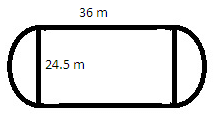
Thus, the area of the playground will be the sum of the area of a rectangle and the areas of the two semicircles with equal diameter 24.5 m.
Now, area of rectangle with length 36m and width 24.5m:
Area of rectangle = length × width = 36m × 24.5 m = 882 m²
Radius of the semicircle = r = 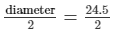 = 12.25m
= 12.25m
∴ Area of the semicircle = 1/2πr²
= 1/2 × 22/7 × (12.25)2 = 235.8 m²
∴ Area of the complete playground = area of the rectangular ground + 2 × area of a semicircle = 882 + 2 × 235.8 = 1353.6 m²
Question 4:
A rectangular piece is 20 m long and 15 m wide. From its four corners, quadrants of radii 3.5 m have been cut. Find the area of the remaining part.
ANSWER:
It is given that the length of the rectangular piece is 20 m and its width is 15 m.And, from each corner a quadrant each of radius 3.5 m has been cut out.A rough figure for this is given below:It is given that the length of the rectangular piece is 20 m and its width is 15 m.And, from each corner a quadrant each of radius 3.5 m has been cut out.A rough figure for this is given below: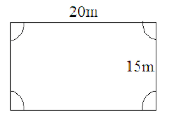
∴ Area of the remaining part = Area of the rectangular piece−(4 × Area of a quadrant of radius 3.5m)
Now, area of the rectangular piece = 20 × 15 = 300 m²
And, area of a quadrant with radius 3.5 m = 1/4πr² = 1/4 × 22/7 × (3.5)2
= 1/4 × 22/7 × 3.5 × 3.5 = 9.625 m²
∴ Area of the remaining part = 300−(4 × 9.625) = 261.5 m²
PAGE NO 20.14:
Question 5:
The inside perimeter of a running track (shown in Fig. 20.24) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If track is everywhere 14 m wide, find the area of the track. Also, find the length of the outer running track.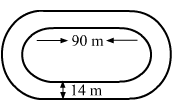
ANSWER:
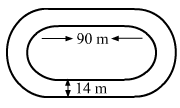
It is given that the inside perimeter of the running track is 400 m. It means the length of the inner track is 400 m.Let r be the radius of the inner semicircles.
Observe: Perimeter of the inner track = Length of two straight portions of 90 m + Length of two semicircles
∴ 400 = (2 × 90) + (2 × Perimiter of a semicircle)400 = 180 + (2 × 22/7 × r)
400−180 = (44/7 × r)
44/7 × r = 220
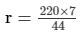 = 35 m
= 35 m
∴ Width of the inner track = 2r = 2 × 35 = 70 m
Since the track is 14 m wide at all places, so the width of the outer track: 70 + (2 × 14) = 98 m
∴ Radius of the outer track semicircles = 98/2 = 49 m
Area of the outer track = (Area of the rectangular portion with sides 90 m and 98 m) + (2 × Area of two semicircles with radius 49 m)
= (98 × 90) + (2 × 1/2 × 22/7 × 492)
= (8820) + (7546)
= 16366 m²
And, area of the inner track = (Area of the rectangular portion with sides 90 m and 70 m) + (2 × Area of the semicircle with radius 35 m)
= (70 × 90) + (2 × 1/2 × 22/7 × 352)
= (6300) + (3850)
= 10150 m²
∴ Area of the running track = Area of the outer track−Area of the inner track
= 16366−10150
= 6216 m²
And, length of the outer track = (2 × length of the straight portion) + (2 × perimeter of the semicircles with radius 49 m)
= (2 × 90) + (2 × 22/7 × 49)
= 180 + 308
= 488 m
Question 6:
Find the area of Fig. 20.25, in square cm, correct to one place of decimal. (Take π = 22/7)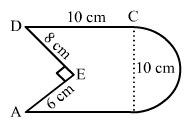
ANSWER:
The given figure is: The given figure is: 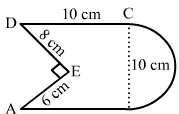
Construction : Connect A to D.Then, we have: Area of the given figure
= (Area of rectangle ABCD + Area of the semicircle) − (Area of Δ AED).
∴ Total area of the figure = (Area of rectangle with sides 10 cm and 10 cm) + (Area of semicircle with radius
= 10/2 = 5 cm)−(Area of triangle AED with base 6 cm and height 8 cm)
= (10 × 10) + (1/2 × 22/7 × 52)−(1/2 × 6 × 8)
= 100 + 39.3−24
= 115.3 cm²
Question 7:
The diameter of a wheel of a bus is 90 cm which makes 315 revolutions per minute. Determine its speed in kilometres per hour. [Use π = 22/7]
ANSWER:
It is given that the diameter of the wheel is 90 cm.
∴ Radius of the circular wheel, r = 90/2 = 45 cm.
∴ Perimeter of the wheel = 2 × π × r = 2 × 22/7 × 45 = 282.857 cm
It means the wheel travels 282.857 cm in a revolution.
Now, it makes 315 revolutions per minute.
∴ Distance travelled by the wheel in one minute = 315 × 282.857 = 89100 cm
∴ Speed = 89100 cm per minute = 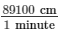
Now, we need to convert it into kilometers per hour.
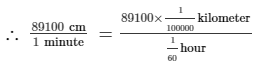
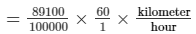
= 53.46 kilometers per hour
Question 8:
The area of a rhombus is 240 cm² and one of the diagonal is 16 cm. Find another diagonal.
ANSWER:
Given:Area of the rhombus = 240 cm Length of one of its diagonals = 16 cm
We know that if the diagonals of a rhombus are d1 and d2, then the area of the rhombus is given by:
Area = 1/2(d1 × d2)
Putting the given values:240 = 1/2(16 × d2)
240 × 2 = 16 × d2
This can be written as follows:16 × d2 = 480
d2 = 480/16
d2 = 30 cm
Thus, the length of the other diagonal of the rhombus is 30 cm.
Question 9:
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
ANSWER:
Given:Lengths of the diagonals of a rhombus are 7.5 cm and 12 cm.
Now, we know:
Area = 1/2(d1 × d2)
∴ Area of rhombus = 1/2(7.5 × 12) = 45 cm²
Question 10:
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
ANSWER:
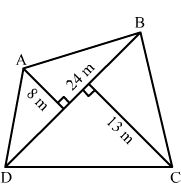
Given: Diagonal of a quadrilateral shaped field = 24 m
Perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m.
Now, we know:
Area = 1/2 × d × (h1 + h2)
∴ Area of the field = 1/2 × 24 × (8 + 13)
= 12 × 21 = 252 m²
Question 11:
Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
ANSWER:
Given: Side of the rhombus = 6 cm
Altitude = 4 cm
One of the diagonals = 8 cm
Area of the rhombus = Side × Altitude = 6 × 4 = 24 cm² ........(i)
We know: Area of rhombus = 1/2 × d1 × d2
Using (i):24 = 1/2 × d1 × d2
24 = 1/2 × 8 × d2
d2 = 6 cm
Question 12:
The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m² is Rs 4.
ANSWER:
Given:The floor consist of 3000 rhombus shaped tiles.The lengths of the diagonals of each tile are 45 cm and 30 cm.
∴ Area of a rhombus shaped tile = 1/2 × (45 × 30) = 675 cm²
∴ Area of the complete floor = 3000 × 675 = 2025000 cm²
Now, we need to convert this area into m² because the rate of polishing is given as per m².
∴ 2025000 cm² = 2025000 × cm × cm
= 2025000 × 1/100 m × 1/100 m
= 202.5 m²
Now, the cost of polishing 1 m² is Rs 4.
∴ Total cost of polishing the complete floor = 202.5 × 4 = 810
Thus, the total cost of polishing the floor is Rs 810.
Question 13:
A rectangular grassy plot is 112 m long and 78 m broad. It has a gravel path 2.5 m wide all around it on the side. Find the area of the path and the cost of constructing it at Rs 4.50 per square metre.
ANSWER:
Given:The length of a rectangular grassy plot is 112 m and its width is 78 m.
Also, it has a gravel path of width 2.5 m around it on the sides .Its rough diagram is given below: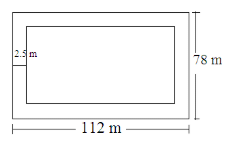
Length of the inner rectangular field = 112−(2 × 2.5) = 107 m
The width of the inner rectangular field = 78−(2 × 2.5) = 73 m
∴ Area of the path = (Area of the rectangle with sides 112 m and 78 m)−(Area of the rectangle with sides 107 m and 73 m)
= (112 × 78)−(107 × 73)
= 8736−7811
= 925 m²
Now, the cost of constructing the path is Rs 4.50 per square meter.
∴ Cost of constructing the complete path = 925 × 4.50 = Rs 4162.5
Thus, the total cost of constructing the path is Rs 4162.5
Question 14:
Find the area of a rhombus, each side of which measures 20 cm and one of whose diagonals is 24 cm.
ANSWER:
Given:Side of the rhombus = 20 cm Length of a diagonal = 24 cm
We know: If d1 and d2 are the lengths of the diagonals of the rhombus, then
side of the rhombus = 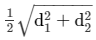
So, using the given data to find the length of the other diagonal of the rhombus:
20 = 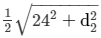
40 = 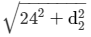
Squaring both sides to get rid of the square root sign:
402 = 242 + d22
d22 = 1600-576 = 1024
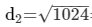 = 32 cm
= 32 cm
∴ Area of the rhombus = 1/2(24 × 32) = 384 cm²
Question 15:
The length of a side of a square field is 4 m. what will be the altitude of the rhombus, if the area of the rhombus is equal to the square field and one of its diagonal is 2 m?
ANSWER:
Given:Length of the square field = 4 m
∴ Area of the square field = 4 × 4 = 16 m²
Given: Area of the rhombus = Area of the square field
Length of one diagonal of the rhombus = 2 m
∴ Side of the rhombus =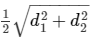
And, area of the rhombus = 1/2 × (d1 × d2)
∴ Area:16 = 1/2(2 × d2)
d2 = 16 m
Now, we need to find the length of the side of the rhombus.
∴ Side of the rhombus = 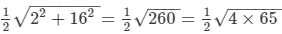
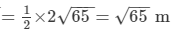
Also, we know: Area of the rhombus = Side × Altitude
∴ 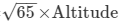
Altitude = 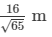
Question 16:
Find the area of the field in the form of a rhombus, if the length of each side be 14 cm and the altitude be 16 cm.
ANSWER:
Given:Length of each side of a field in the shape of a rhombus = 14 cm
Altitude = 16 cm
Now, we know: Area of the rhombus = Side × Altitude
∴ Area of the field = 14 × 16 = 224 cm²
Question 17:
The cost of fencing a square field at 60 paise per metre is Rs 1200. Find the cost of reaping the field at the rate of 50 paise per 100 sq. metres.
ANSWER:
Given:Cost of fencing 1 metre of a square field = 60 paise
And, the total cost of fencing the entire field = Rs 1200 = 1,20,000 paise
∴ Perimeter of the square field = 120000/60 = 2000 metres
Now, perimeter of a square = 4 × side
For the given square field:4 × Side = 2000 m
Side = 2000/4 = 500 metres
∴ Area of the square field = 500 × 500 = 250000 m²
Again, given: Cost of reaping per 100 m² = 50 paise
∴ Cost of reaping per 1 m² = 50/100paise
∴ Cost of reaping 250000 m² = 50/100 × 250000 = 125000 paise
Thus, the total cost of reaping the complete square field is 125000 paise,
i.e. Rs 1250.
Question 18:
In exchange of a square plot one of whose sides is 84 m, a man wants to buy a rectangular plot 144 m long and of the same area as of the square plot. Find the width of the rectangular plot.
ANSWER:
Given:Side of the square plot = 84 m
Now, the man wants to exchange it with a rectangular plot of the same area with length 144.
Area of the square plot = 84 × 84 = 7056 m²
∴ Area of the rectangular plot = Length × Width
7056 = 144 × Width
⇒Width = 7056/144 = 49 m
Hence, the width of the rectangular plot is 49 m.
Question 19:
The area of a rhombus is 84 m². If its perimeter is 40 m, then find its altitude.
ANSWER:
Given:Area of the rhombus = 84 m²
Perimeter = 40 m
Now, we know: Perimeter of the rhombus = 4 × Side
∴ 40 = 4 × Side
Side = 40/4 = 10 m
Again, we know:
Area of the rhombus = Side × Altitude
⇒ 84 = 10 × Altitude
Altitude = 84/10 = 8.4 m
Hence, the altitude of the rhombus is 8.4 m.
Question 20:
A garden is in the form of a rhombus whose side is 30 metres and the corresponding altitude is 16 m. Find the cost of levelling the garden at the rate of Rs 2 per m².
ANSWER:
Given:Side of the rhombus shaped garden = 30 m
Altitude = 16 m
Now, area of a rhombus = side × altitude
∴ Area of the given garden = 30 × 16 = 480 m²
Also, it is given that the rate of levelling the garden is Rs 2 per 1m².
∴ Total cost of levelling the complete garden of area 480 m² = 480 × 2 = Rs 960
Question 21:
A field in the form of a rhombus has each side of length 64 m and altitude 16 m. What is the side of a square field which has the same area as that of a rhombus?
ANSWER:
Given:Each side of a rhombus shaped field = 64 m
Altitude = 16 m
We know: Area of rhombus = Side × Altitude
∴ Area of the field = 64 × 16 = 1024 m²
Given: Area of the square field = Area of the rhombus
We know: Area of a square = (Side)2
∴ 1024 = (Side)2
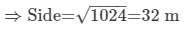
Thus, the side of the square field is 32 m.
PAGE NO 20.15:
Question 22:
The area of a rhombus is equal to the area of a triangle whose base and the corresponding altitude are 24.8 cm and 16.5 cm respectively. If one of the diagonals of the rhombus is 22 cm, find the length of the other diagonal.
ANSWER:
Given: Area of the rhombus = Area of the triangle with base 24.8 cm and altitude 16.5 cm
Area of the triangle = 1/2 × base × altitude
= 1/2 × 24.8 × 16.5
= 204.6 cm²
∴ Area of the rhombus = 204.6 cm²
Also, length of one of the diagonals of the rhombus = 22 cm
We know: Area of rhombus = 1/2(d1 × d2)
204.6 = 1/2(22 × d2)
22 × d2 = 409.2
d2 = 409.2/22 = 18.6 cm
Hence, the length of the other diagonal of the rhombus is 18.6 cm.
FAQs on Chapter 20 - Mensuration - I (Part - 1), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What are the different types of mensuration covered in Chapter 20 of RD Sharma Class 8 Maths? |  |
| 2. How can I find the area of a rectangle using the concepts discussed in Chapter 20 of RD Sharma Class 8 Maths? |  |
| 3. What is the formula to find the volume of a cube according to RD Sharma Class 8 Maths Chapter 20? |  |
| 4. Can RD Sharma Class 8 Maths Chapter 20 help in calculating the perimeter of a circle? |  |
| 5. How can I find the area of a triangle using the concepts explained in RD Sharma Class 8 Maths Chapter 20? |  |
















