NCERT Exemplar: Introduction to Three Dimensional Geometry | Mathematics (Maths) Class 11 - Commerce PDF Download
SHORT ANSWERS TYPE QUESTIONS
Q.1. Locate the following points:
(i) (1, – 1, 3)
(ii) (– 1, 2, 4)
(iii) (– 2, – 4, –7)
(iv) (– 4, 2, – 5)
Ans.
(i) Location of P(1, – 1, 3) = (x, – y, z) = IV octant
(ii) Location of Q(– 1, 2, 4) = (– x, y, z) = II octant
(iii) Location of R(– 2, – 4, – 7) = (– x, – y, – z) = VII octant
(iv) Location of S(– 4, 2, – 5) = (– x, y, – z) = VI octant
Q.2. Name the octant in which each of the following points lies.
(i) (1, 2, 3)
(ii) (4, – 2, 3)
(iii) (4, –2, –5)
(iv) (4, 2, –5)
(v) (– 4, 2, 5)
(vi) (–3, –1, 6)
(vii) (2, – 4, – 7)
(viii) (– 4, 2, – 5)
Ans.
(i) Point (1, 2, 3) lies in I octant
(ii) Point (4, – 2, 3) lies in IV octant
(iii) Point (4, – 2, – 5) lies in VIII octant
(iv) Point (4, 2, – 5) lies in V octant
(v) Point (– 4, 2, 5) lies in II octant
(vi) Point (– 3, – 1, 6) lies in III octant
(vii) Point (2, – 4, – 7) lies in VIII octant
(viii) Point (– 4, 2, – 5) lies in VI octant
Q.3. Let A, B, C be the feet of perpendiculars from a point P on the x, y, z-axis respectively. Find the coordinates of A, B and C in each of the following where the point P is :
(i) A = (3, 4, 2)
(ii) (–5, 3, 7)
(iii) (4, – 3, – 5)
Ans.
The coordinates of A, B and C are
(i) A(3, 0, 0), B(0, 4, 0) and C(0, 0, 2)
(ii) A(– 5, 0, 0), B(0, 3, 0) and C(0, 0, 7)
(iii) A(4, 0, 0), B(0, – 3, 0) and C(0, 0, – 5)
Q.4. Let A, B, C be the feet of perpendiculars from a point P on the xy, yz and zx planes respectively. Find the coordinates of A, B, C in each of the following where the point P is
(i) (3, 4, 5)
(ii) (–5, 3, 7)
(iii) (4, – 3, – 5).
Ans.
The coordinates of A, B and C are
(i) A(3, 4, 0), B(0, 4, 5) and C(3, 0, 5)
(ii) A(– 5, 3, 0), B(0, 3, 7) and C(– 5, 0, 7)
(iii) A(4, – 3, 0), B(0, – 3, – 5) and C(4, 0, – 5)
Q.5. How far apart are the points (2, 0, 0) and (–3, 0, 0)?
Ans. Given points are (2, 0, 0) and (– 3, 0, 0)
∴ Distance between the given points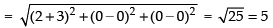
Hence, the required distance = 5.
Q.6. Find the distance from the origin to (6, 6, 7).
Ans. Coordinates of the origin are (0, 0, 0)
∴ Distance from (0, 0, 0) to (6, 6, 7)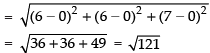
= 11 units.
Hence, the required distance = 11 units.
Q.7. Show that if x2 + y2 = 1, then the point (x, y,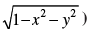 is at a distance 1 unit from the origin.
is at a distance 1 unit from the origin.
Ans. Given point is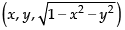
∴ Distance between the origin and the point is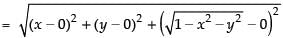
= √1 = 1 .
Hence, proved.
Q.8. Show that the point A (1, – 1, 3), B (2, – 4, 5) and (5, – 13, 11) are collinear.
Ans. Given points are A(1, – 1, 3), B(2, – 4, 5) and C(5, – 13, 11)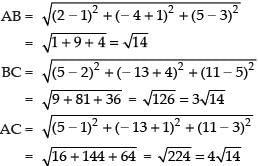
Here we observe that √14 + 3√14 = 4√14
So AB + BC = AC.
Hence, the given points are collinear.
Q.9. Three consecutive vertices of a parallelogram ABCD are A (6, – 2, 4), B (2, 4, – 8), C (–2, 2, 4). Find the coordinates of the fourth vertex.
[Hint: Diagonals of a parallelogram have the same mid-point.]
Ans. Let the coordinates of the fourth vertex be (a, b, c)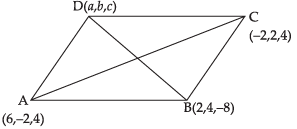
We know that the diagonals of a parallelogram bisect each other.
∴ Mid-point of diagonal AC =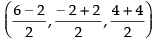
and the mid-point of diagonal BD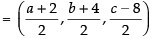
∴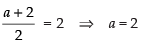
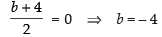
and 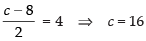
Hence, the required coordinates are (2, – 4, 16).
Q.10. Show that the triangle ABC with vertices A (0, 4, 1), B (2, 3, – 1) and C (4, 5, 0) is right angled.
Ans. Given vertices are A(0, 4, 1), B(2, 3, – 1) and C(4, 5, 0)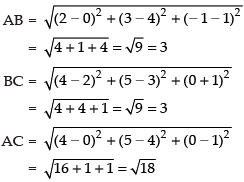
∵ (3)2 + (3)2 = (√18)2 .
So AB2 + BC2 = AC2
Hence, ΔABC is a right angled triangle.
Q.11. Find the third vertex of triangle whose centroid is origin and two vertices are (2, 4, 6) and (0, –2, –5).
Ans. Let the coordinates of the third vertex i.e. A be (a, b, c).
Since the centroid is at origin i.e. (0, 0, 0)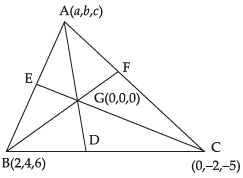
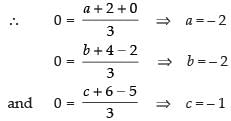
Hence, the required coordinates are (– 2, – 2, – 1).
Q.12. Find the centroid of a triangle, the mid-point of whose sides are D (1, 2, – 3), E (3, 0, 1) and F (– 1, 1, – 4).
Ans. Let the coordinates of the vertices of ΔABC be
A(x1, y1, z1), B(x2, y2, z2) and C(x3, y3, z3).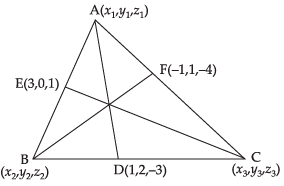
Mid-point of BC = (1, 2, – 3)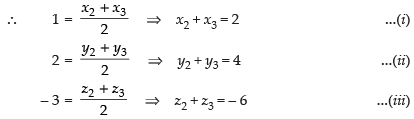
Mid-point of AB = (3, 0, 1)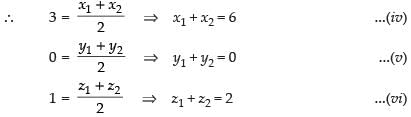
Similarly, mid-point of AC = (– 1, 1, – 4)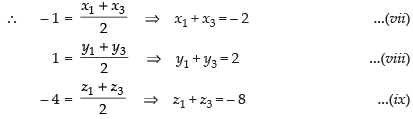
Adding eq. (i), (iv) and (vii) we get,
2x1 + 2x2 + 2x3 = 2 + 6 – 2 = 6
⇒ x1 + x2 + x3 = 3
⇒ 6 + x3 = 3 ⇒ x3 = – 3 [from eq. (iv)]
⇒ x1 + 2 = 3 ⇒ x1 = 1 [from eq. (i)]
⇒ x2 – 2 = 3 ⇒ x2 = 5 [from eq. (vii)]
So, x1 = 1, x2 = 5 and x3 = – 3.
Similarly, Adding (ii), (v) and (viii) we get
2(y1 + y2 + y3) = 4 + 0 + 2 = 6
∴ y1 + y2 + y3 = 3
y1 + 4 = 3 ⇒ y1 = – 1
0 + y3 = 3 ⇒ y3 = 3
y2 + 2 = 3 ⇒ y2 = 1
So, y1 = – 1, y2 = 1, y3 = 3
Adding (iii), (vi) and (ix) we have
2(z1 + z2 + z3) = – 6 + 2 – 8 = – 12
∴ z1 + z2 + z3 = – 6
z1 – 6 = – 6 ⇒ z1 = 0 [from eq. (iii)]
2 + z3 = – 6 ⇒ z3 = – 8 [from eq. (vi)]
and z2 – 8 = – 6 ⇒ z2 = 2
∴ z1 = 1, z2 = 1, z3 = - 8.
So, the points are A(1, – 1, 0), B(5, 1, 2) and C(– 3, 3, – 8).
∴ Centroid of the triangle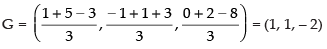
Hence, the required coordinates = (1, 1, – 2).
Q.13. The mid-points of the sides of a triangle are (5, 7, 11), (0, 8, 5) and (2, 3, – 1). Find its vertices.
Ans. Let the coordinates of the vertices be A
(x1, y1, z1), B(x2, y2, z2) and C(x3, y3, z3) respectively.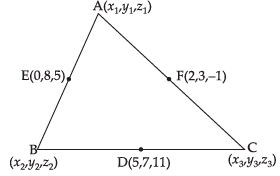
Since D(5, 7, 11) is the mid-point of BC
E(0, 8, 5) is the mid-point of AB
Similarly, F(2, 3, – 1) is the mid-point of AC
Adding eq. (i), (iv) and (vii) we get
2(x1 + x2 + x3) = 10 + 0 + 4
⇒ x1 + x2 + x3 = 7 ...(x)
Subtracting (i) from (x) we get,
x1 = 7 – 10 = – 3
Subtracting eq. (iv) from (x) we get
x3 = 7 – 0 = 7
Subtracting eq. (vii) from (x) we get
x2 = 7 – 4 = 3
Adding eq. (ii), (v) and (viii) we get
2(y1 + y2 + y3) = (14 + 16 + 6)
⇒ y1 + y2 + y3 = 18 ...(xi)
Subtracting eq. (ii) from (xi) we get
y1 = 18 – 14 = 4
Subtracting eq. (v) from (xi) we get
y3 = 18 – 16 = 2
Subtracting eq. (viii) from (xi) we get
y2 = 18 – 6 = 12
Now adding eq. (iii), (vi) and (ix) we get
2(z1 + z2 + z3) = 22 + 10 – 2
⇒ z1 + z2 + z3 = 15 ...(xii)
Subtracting eq. (iii) from (xii) we get
z1 = 15 – 22 = – 7
Subtracting eq. (vi) from (xii), we get
z3 = 15 – 10 = 5
Subtracting eq. (ix) from (xii) we get
z2 = 15 + 2 = 17
So, the required coordinates are
A(x1, y1, z1), B(x2, y2, z2) and C(x3, y3, z3).
i.e. A(– 3, 4, – 7), B(3, 12, 17) and C(7, 2, 5).
Q.14. Three vertices of a Parallelogram ABCD are A (1, 2, 3), B (– 1, – 2, – 1) and C (2, 3, 2). Find the fourth vertex D.
Ans. Let the coordinates of D be (a, b, c).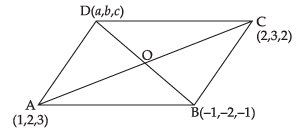
We know that the diagonals of a parallelogram bisect each other.
∴ Mid-point of AC i.e. O =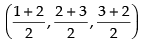
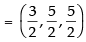
Mid-point of BD i.e.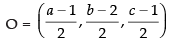
Equating the corresponding coordinate, we have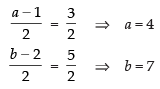
and 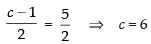
Hence, the coordinates of D = (4, 7, 6).
Q.15. Find the coordinate of the points which trisect the line segment joining the points A (2, 1, – 3) and B (5, – 8, 3).
Ans. Let C and D be the points which divide the given line AB into three equal parts.
Here AC : CB = 1 : 2
Let (x1, y1, z1) be the coordinates of C
∴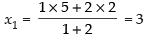
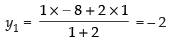
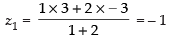
So C = (3, – 2, – 1).
Now D is the mid-point = CB
Let the coordinates of D be (x2, y2, z2)
∴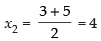
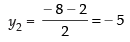
and 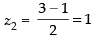
So, D = (4, – 5, 1).
Hence, the required coordinates are
C(3, – 2, – 1) and D(4, – 5, 1).
Q.16. If the origin is the centriod of a triangle ABC having vertices A (a, 1, 3), B (– 2, b, – 5) and C (4, 7, c), find the values of a, b, c.
Ans. Coordinates of the centroid G = (0, 0, 0)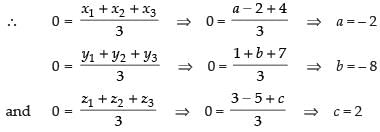
Hence, the required values are a = – 2, b = – 8 and c = 2.
Q.17. Let A (2, 2, – 3), B (5, 6, 9) and C (2, 7, 9) be the vertices of a triangle. The internal bisector of the angle A meets BC at the point D. Find the coordinates of D.
Ans. Given that AD is the internal bisector of ∠A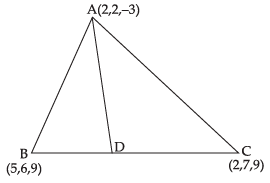
∴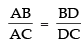
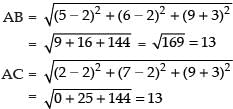
∴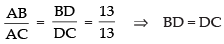
⇒ D is the mid-point of BC
∴ Coordinates of D =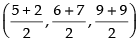
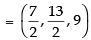
Hence, the required coordinates are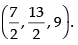
LONG ANSWERS TYPE QUESTIONS
Q.18. Show that the three points A (2, 3, 4), B (–1, 2, – 3) and C (– 4, 1, – 10) are collinear and find the ratio in which C divides AB.
Ans. Given points are A(2, 3, 4), B(– 1, 2, – 3) and C(– 4, 1, – 10)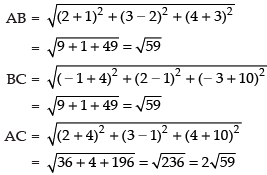
∴ AB + BC = AC
√59 + √59 = 2√59
Hence, A, B and C are collinear and AC : BC = 2√ 59 : √59 = 2 : 1
Hence, C divides AB is 2 : 1 externally.
Q.19. The mid-point of the sides of a triangle are (1, 5, – 1), (0, 4, – 2) and (2, 3, 4). Find its vertices. Also find the centriod of the triangle.
Ans. Let the vertices of the given triangle be
A(x1, y1, z1), B(x2, y2, z2) and C(x3, y3, z3).
D is the mid-point of BC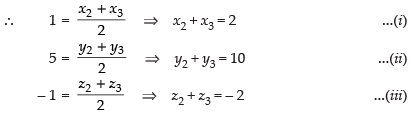
E is the mid-point of AB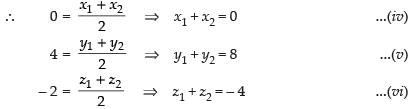
F is the mid-point of AC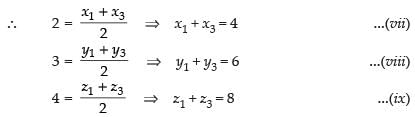
Adding eq. (i), (iv) and (vii) we get
2(x1 + x2 + x3) = 2 + 0 + 4
∴ x1 + x2 + x3 = 3 ...(x)
Adding (ii), (v) and (viii) we get
2(y1 + y2 + y3) = 10 + 8 + 6
⇒ y1 + y2 + y3 = 12 ...(xi)
Adding (iii), (vi) and (ix) we get
2(z1 + z2 + z3) = – 2 – 4 + 8
∴ z1 + z2 + z3 = 1 ...(xii)
Subtracting eq. (i) from (x) we get
x1 = 3 – 2 = 1 ⇒ x1 = 1
Subtracting eq. (ii) from (xi) we get
y1 = 12 – 10 = 2 ⇒ y1 = 2
Subtracting eq. (iii) from (xii) we get
z1 = 1 – (– 2) = 3 ⇒ z1 = 3
Hence, the coordinates of A = (1, 2, 3)
Subtracting eq. (iv) from (x) we get
x3 = 3 – 0 = 3 ⇒ x3 = 3
Subtracting eq. (v) from (xi) we get
y3 = 12 – 8 = 4 ⇒ y3 = 4
Subtracting eq. (vi) from (xii) we get
z3 = 1 – (– 4) = 5 ⇒ z3 = 5
Here the coordinates of C = (3, 4, 5)
Subtracting eq. (vii) from (x) we get
x2 = 3 – 4 = – 1 ⇒ x2 = – 1
Subtracting eq. (viii) from (xi) we get
y2 = 12 – 6 = 6 ⇒ y2 = 6
Subtracting eq. (ix) from (xii) we get
z2 = 1 – 8 = – 7 ⇒ z2 = – 7
Here, the coordinates of B(– 1, 6, – 7)
Hence, the required coordinates are
A(1, 2, 3), B(– 1, 6, – 7) and C(3, 4, 5)
and Centroid G =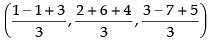
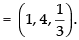
Q.20. Prove that the points (0, – 1, – 7), (2, 1, – 9) and (6, 5, – 13) are collinear. Find the ratio in which the first point divides the join of the other two.
Ans. Let the given points are A(0, – 1, – 7), B(2, 1, – 9) and C(6, 5, – 13)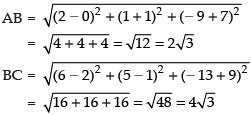
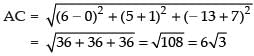
2 √3 + 4 √3 = 6 √3
i.e. AB + BC = AC
∴ AB : AC = 2 √3 : 6√ 3 = 1 : 3
Hence, point A divides B and C in 1 : 3 externally.
Q.21. What are the coordinates of the vertices of a cube whose edge is 2 units, one of whose vertices coincides with the origin and the three edges passing through the origin, coincides with the positive direction of the axes through the origin?
Ans. Given that each edge of the cuboid is 2 units.
∴ Coordinaates of the vertices are
A(2, 0, 0), B(2, 2, 0), C(0, 2, 0),
D(0, 2, 2), E(0, 0, 2), F(2, 0, 2),
G(2, 2, 2) and O(0, 0, 0).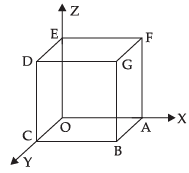
OBJECTIVE ANSWERS TYPE QUESTIONS
Q.22. The distance of point P(3, 4, 5) from the yz-plane is
(a) 3 units
(b) 4 units
(c) 5 units
(d) 550
Ans. (a)
Solution.
Given point is P(3, 4, 5)
∴ Distance of P from yz-plane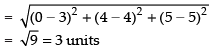
Hence, the correct option is (a).
Q.23. What is the length of foot of perpendicular drawn from the point P(3, 4, 5) on y-axis?
(a) √41
(b) √34
(c) 5
(d) None of these
Ans. (b)
Solution.
On y-axis, x = 0 and z = 0 and given point P(3, 4, 5)
∴ The point A is (0, 4, 0)
∴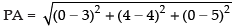
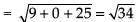
Hence, the correct option is (b).
Q.24. Distance of the point (3, 4, 5) from the origin (0, 0, 0) is
(a) √50
(b) 3
(c) 4
(d) 5
Ans. (a)
Solution.
Given points A(3, 4, 5) and the given O(0, 0, 0)
∴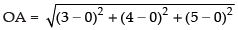
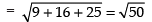
Hence, the correct option is (a).
Q.25. If the distance between the points (a, 0, 1) and (0, 1, 2) is √27, then the value of ‘a’ is
(a) 5
(b) ± 5
(c) – 5
(d) None of these
Ans. (b)
Solution.
Let the given points be A(a, 0, 1) and B(0, 1, 2)
∴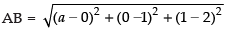
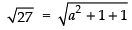
Squaring both sides, we get
27 = a2 + 2 ⇒ a2 = 25 ∴ a = ± 5
Hence, the correct option is (b).
Q.26. x-axis is the intersection of two planes.
(a) xy and xz
(b) yz and zx
(c) xy and yz
(d) None of these
Ans. (a)
Solution.
We know that on the xy and xz-planes, the line of intersection is x-axis.
Hence, the correct option is (a).
Q.27. Equation of y-axis is considered as
(a) x = 0, y = 0
(b) y = 0, z = 0
(c) z = 0, x = 0
(d) None of these
Ans. (c)
Solution.
On y-axis, x = 0 and z = 0
Hence, the correct option is (c).
Q.28. The point (– 2, – 3, – 4) lies in the
(a) first octant
(b) seventh octant
(c) second octant
(d) eighth octant
Ans. (b)
Solution.
The point (– 2, – 3, – 4) lies in seventh octant.
Hence, the correct option is (b).
Q.29. A plane is parallel to yz-plane, so it is perpendicular to
(a) x-axis
(b) y-axis
(c) z-axis
(d) None of these
Ans. (a)
Solution.
Any plane parallel to yz-plane is perpendicular to x-axis.
Hence, the correct option is (a).
Q.30. The locus of a point for which y = 0, z = 0 is
(a) equation of x-axis
(b) equation of y-axis
(c) equation of z-axis
(d) None of these
Ans. (a)
Solution.
We know that one equation of x-axis, y = 0, z = 0
Hence, the locus of the point is equation of x-axis.
So, the correct option is (a).
Q.31. The locus of a point for which x = 0 is
(a) xy-plane
(b) yz-plane
(c) zx-plane
(d) None of these
Ans. (b)
Solution.
On the yz-plane, x = 0
Hence, the locus of the point is yz-plane.
So, the correct option is (b).
Q.32. If a parallelopiped is formed by planes drawn through the points (5, 8, 10) and (3, 6, 8) parallel to the coordinate planes, then the length of diagonal of the parallelopiped is
(a) 2√3
(b) 3√2
(c) √2
(d) √3
Ans. (a)
Solution.
Given points are A(5, 8, 10) and B(3, 6, 8)
∴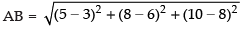
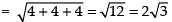
Hence, the correct option is (a).
Q.33. L is the foot of perpendicular drawn from a point P(3, 4, 5) on xy-plane. The coordinate of point L are
(a) (3, 0, 0)
(b) (0, 4, 5)
(c) (3, 0, 5)
(d) None of these
Ans. (d)
Solution.
We know that on xy-plane, z = 0.
So, the coordinate of the point L are (3, 4, 0).
Hence, the correct option is (d).
Q.34. L is the foot of the perpendicular drawn from point (3, 4, 5) on X-axis. The coordinates of L are
(a) (3, 0, 0)
(b) (0, 4, 0)
(c) (0, 0, 5)
(d) None of these
Ans. (a)
Solution.
We know that x-axis, y = 0 and z = 0.
So, the required coordinates are (3, 0, 0).
Hence, the correct option is (a).
FILL IN THE BLANKS
Q.35. The three axes OX, OY, OZ determine ________ .
Ans. The three axes OX, OY and OZ determine three coordinate planes.
Hence, the filler value is three coordinate planes.
Q.36. The three planes determine a rectangular parallelopiped which has ________ of rectangular faces.
Ans. Three pairs.
Hence, the value of the filler is three pairs.
Q.37. The coordinates of a point are the perpendicular distance from the ________ on the respectives axes.
Ans. Given points.
Hence, the value of the filler is given points.
Q.38. The three coordinate planes divide the space into ________ parts.
Ans. Eight.
Hence, the values of the filler is eight.
Q.39. If a point P lies in yz-plane, then the coordinates of a point on yz-plane is of the form ________.
Ans. We know that on yz-plane, x = 0
So, the coordinates of the required point is (0, y, z).
Hence, the value of the filler is (0, y, z).
Q.40. The equation of yz-plane is ________.
Ans. The equation of yz-plane is x = 0.
Hence, the value of the filler is x = 0.
Q.41. If the point P lies on z-axis, then coordinates of P are of the form ________.
Ans. On the z-axis, x = 0 and y = 0.
∴ The required coordinate is in the form of (0, 0, z).
Hence, the value of the filler is (0, 0, z).
Q.42. The equation of z-axis, are ________.
Ans. The equation of z-axis are, x = 0 and y = 0.
Hence, the value of the filler is x = 0 and y = 0.
Q.43. A line is parallel to xy-plane if all the points on the line have equal ________.
Ans. z-coordinates
Hence, the value of the filler is z-coordinates.
Q.44. A line is parallel to x-axis if all the points on the line have equal ________.
Ans. y and z coordinates.
Hence, the value of the filler is y and z coordinates.
Q.45. x = a represent a plane parallel to ________.
Ans. x = a represents a plane parallel to yz-plane.
Q.46. The plane parallel to yz - plane is perpendicular to ________.
Ans. The plane parallel to yz-plane is perpendicular to x-axis.
Hence, the value of the filler is x-axis.
Q.47. The length of the longest piece of a string that can be stretched straight in a rectangular room whose dimensions are 10, 13 and 8 units are ______.
Ans. The given dimensions are 10, 13 and 8
Let a = 10, b = 13 and c = 8
∴ Required length =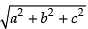
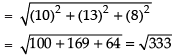
Hence, the value of the filler is √333 .
Q.48. If the distance between the points (a, 2, 1) and (1, –1, 1) is 5, then a _______.
Ans. Given points are (a, 2, 1) and (1, – 1, 1)
∴ Distance =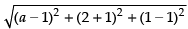
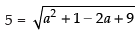
Squaring both sides, we have
25 = a2 – 2a + 10
⇒ a2 – 2a – 15 = 0
⇒ a2 - 5a + 3a - 15 = 0
⇒ a(a - 5) + 3(a - 5) = 0
⇒ (a + 3)(a - 5) = 0
∴ a = – 3 or 5
Hence, the value of the filler is 5 or – 3.
Q.49. If the mid-points of the sides of a triangle AB; BC; CA are D (1, 2, – 3), E (3, 0, 1) and F (–1, 1, – 4), then the centriod of the triangle ABC is ________.
Ans. Let the vertices of the ΔABC be
A(x1, y1, z1), B(x2, y2, z2) and C(x3, y3, z3).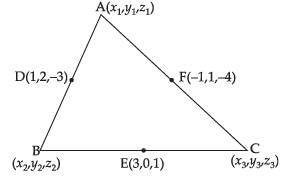
D is the mid-point of AB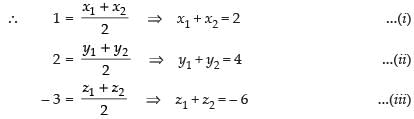
E is the mid-point of BC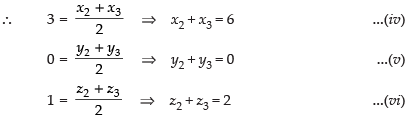
F is the mid-point of AC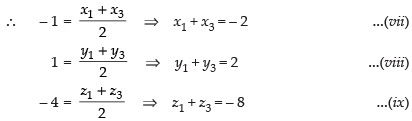
Adding eq. (i), (iv) and (vii) we get
2(x1 + x2 + x3) = 2 + 6 – 2
∴ x1 + x2 + x3 = 3 ...(x)
Adding (ii), (v) and (viii) we get
2(y1 + y2 + y3) = 4 + 0 + 2
⇒ y1 + y2 + y3 = 3 ...(xi)
Adding (iii), (vi) and (ix) we get
2(z1 + z2 + z3) = – 6 + 2 – 8
∴ z1 + z2 + z3 = – 6 ...(xii)
Subtracting (i) from eq. (x) we get
x3 = 3 – 2 = 1 ⇒ x3 = 1
Subtracting (iv) from eq. (x) we get
x1 = 3 – 6 = – 3 ⇒ x1 = – 3
Subtracting (vii) from eq. (x) we get
x2 = 3 – (– 2) = 5 ⇒ x2 = 5
Subtracting (ii) from eq. (xi) we get
y3 = 3 – 4 = – 1 ⇒ y3 = – 1
Subtracting (viii) from eq. (xi) we get
y2 = 3 – 2 = 1 ⇒ y2 = 1
Subtracting (v) from eq. (xi) we get
y1 = 3 – 0 = 3 ⇒ y1 = 3
Subtracting (iii) from eq. (xii) we get
z3 = – 6 – (– 6) = 0 ⇒ z3 = 0
Subtracting (vi) from eq. (xii) we get
z1 = – 6 – 2 = – 8 ⇒ z1 = – 8
Subtracting (ix) from eq. (xii) we get
z2 = – 6 – (– 8) = 2 ⇒ z2 = 2
So, the coordinates are A(– 3, 3, – 8), B(5, 1, 2) and C(1, – 1, 0)
∴ Centroid G =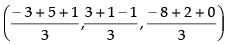
= (1, 1, – 2)
Hence, the value of the filler is (1, 1, – 2).
Q.50. Match each item given under the column C1 to its correct answer given under column C2.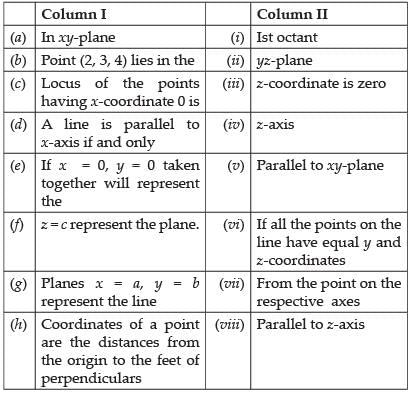
Ans.
(a) In xy-plane, z-coordinate is zero.
Hence, (a) ↔ (iii).
(b) The point (2, 3, 4) lies in first octant.
Hence, (b) ↔ (i).
(c) Locus of the points with x-coordinate is zero is yz-plane.
Hence, (c) ↔ (ii).
(d) A line is parallel to x-axis if and only if all the points on the line have equal y and z-coordinates.
Hence, (d) ↔ (vi).
(e) x = 0, y = 0 represent z-axis.
Hence, (e) ↔ (iv).
(f) z = c represent a plane parallel to xy-plane.
Hence, (f) ↔ (v).
(g) The planes x = a, y = b represent the line parallel to z-axis.
Hence, (g) ↔ (viii).
(h) Coordinates of a point are the distances from the origin to the feet of perpendicular from the point on the respective axes.
Hence, (h) ↔ (vii).
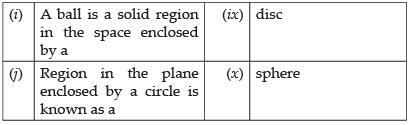
(i) A ball is solid region in the space enclosed by a sphere.
Hence, (i) ↔ (x).
(j) The region in the plane enclosed by a circle is known as a disc.
Hence, (j) ↔ (ix).
|
73 videos|264 docs|91 tests
|
















