EXERCISE 10.2
Question 1. Look at the given map of a city.
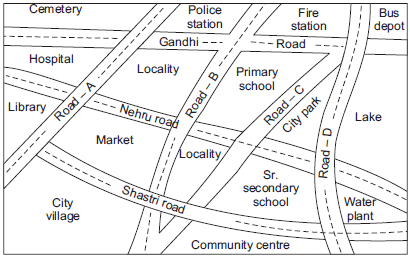
Answer the following.
(a) Colour the map as follows: Blue-water, red-fire station, orange-library, yellow-schools, Green-park, Pink-College, Purple-Hospital, Brown-Cemetery.
(b) Mark a green ‘X’ at the intersection of Road ‘C’ and Nehru Road, Green ‘Y’ at the intersection of Gandhi Road and Road A.
(c) In red, draw a short street route from library to the bus depot.
(d) Which is further east, the city park or the market?
(e) Which is further south, the primary school or the Sr. Secondary School?
Solution: The shaded (coloured) map according to the required directions is given in part (a). Here various colours are as under
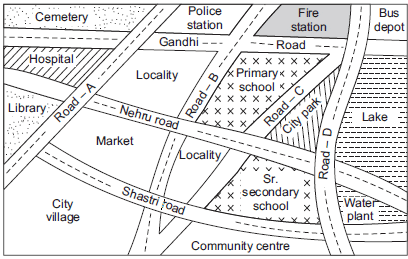
(b) Do as directed.
(c) Do as directed.
(d) City park
(e) Senior Secondary school
Question 2. Draw a map of your class using proper scale and symbols for different objects.
Solution: An activity, do it yourself.
Question 3. Draw a map of your school compound using proper scale and symbols for various features like play ground main building, garden, etc.
Solution: It is an activity. Please do it yourself.
Question 4. Draw a map giving instructions to your friend so that she reaches your house without any difficulty.
Solution:It is an activity. Please do it yourself.
FACES, EDGES AND VERTICES
Note: I. A polygon is a 2-D shape made of line segments only.
II. A polyhedron is a 3-D shape made of plane faces.
III. Plural of polyhedron is polyhedra.
IV. A cube, cuboid, pyramid, prism, etc., are polyhedra whereas spheres, cones and cylinders are not polyhydra.
A cuboid has 6 faces, 12 edges and 8 vertices.
Regular Polyhedron: A convex polyhedron is said to be regular if its faces are made up of regular polygons and the same number faces meet at each vertex.
Note: Regular polyhedra are also called platonic solids.
Prism: Prisms are polyhedra whose top and base are congruent polygons and the other faces are parallelograms.
Pyramids: Pyramids are polyhedra with a polygon at its base and all other faces as triangles meeting in a common vertex.
Note: The prisms and pyramids are named after their bases.
EULER’S FORMULA
It is a relation between the faces edges and vertices of a polyhedra. It is given by
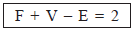
where
F → Number of faces
V → Number of vertices
E → Number of edges.
SOLUTION TO THINK, DISCUSS AND WRITE
Question: What happens to F, V and E if some parts are sliced off from a solid? (To start with, you may take a plasticine cube, cut a corner off and investigate).
Solution: Consider the following cuboid ABCDEFGH:
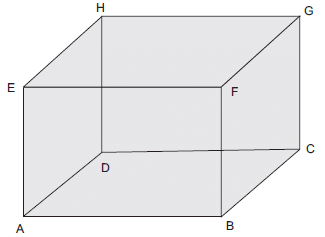
Case I: The given cuboid has:
(i) Number of faces (F) = 6
(ii) Number of vertices (V) = 8
(iii) Number of edges (E) = 12
We have, F + V = 6 + 8 = 14
F + V – E = 14 – 12 = 2
i.e. F + V – E = 2
or the Euler’s formula is verified.
Case II: [A part is sliced off]
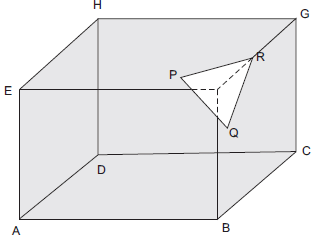
We have:
Number of faces (F) = 7
Number of vertices (V) = 10
Number of Edges (E) = 15
Also F + V = 7 + 10 = 17
and F + V – E = 17 – 15 = 2
Here also, Euler’s formula holds true.
EXERCISE 10.3
Question 1. Can a polyhedron have for its faces
(i) 3 triangles?
(ii) 4 triangles?
(iii) a square and four triangles?
Solution: A polyhedron is bounded by four or more than four polygonal faces.
∴ (i) No, it is not possible that a polyhedron has 3 triangles for its faces.
(ii) Yes, 4 triangles can be the faces of a polyhedron.
(iii) Yes, a square and 4 triangles can be the faces of a polyhedron.
Question 2. Is it possible to have a polyhedron with any given number of faces? Hint: Think of a pyramid.
Solution: Yes, it can be possible only if the number of faces is four or more than four.
Question 3. Which are prisms among the following?
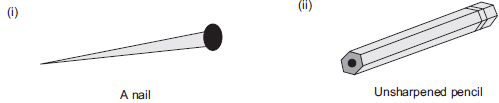
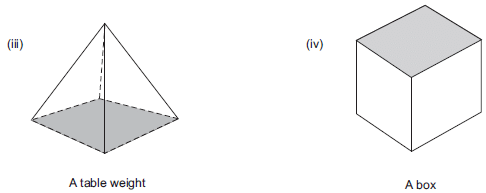
Solution: Since, a prism is a polyhedron having two of its faces congruent and parallel, where as other faces are parallelogram.
∴ (i) No, a nail is not a prism.
(ii) Yes, unsharpened pencil is a prism.
(iii) No, table weight is not a prism.
(iv) Yes, box is a prism.
Question 4. (i) How are prisms and cylinders alike?
(ii) How are pyramids and cones alike?
Solution: (i) Both of the prisms and cylinders have their base and top as congruent faces and parallel to each other. Also, a prism becomes a cylinder as the number of sides of its base becomes larger and larger.
(ii) The pyramid and cones are alike becomes their lateral faces meet at a vertex. Also a pyramid becomes a cone as the number of sides of its base becomes larger and larger.
Question 5. Is a square prism same as a cube? Explain.
Solution: No, not always, because it can be a cuboid also.
Question 6. Verify Euler’s formula for these solids.
: 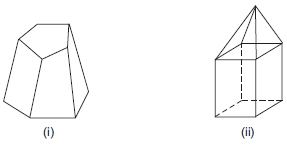
Solution: (i) In figure (i), we have
F = 7, V = 10 and E = 15
∴ F + V = 7 + 10 = 17
F + V – E = 17 – 15 = 2
i.e. F + V – E = 2
Thus, Euler’s formula is verified.
(ii) In figure (ii), we have
F = 9, V = 9 and E = 16
∴ F + V = 9 + 9 = 18
and F + V – E = 18 – 16 = 2
i.e. F + V – E = 2
Thus, Euler’s formula is verified.
Question 7. Using Euler’s formula find the unknown.

Solution: (i) Here, V = 6 and E = 12
Since F + V – E = 2
∴ F + 6 – 12 = 2
or F – 6 = 2
or F = 2 + 6 = 8
(ii) Here, F = 5 and E = 9
Since F + V – E = 2
or 5 + V – 9 = 2
or V – 4 = 2
or v = 2 + 4 = 6
(iii) Here F = 20 V = 12
Since, F + V – E = 2
∴ 20 + 12 – E = 2
or 20 + 12 – E = 2
32 – E = 2
or E = 32 – 2 = 30
Question 8. Can polyhedron have 10 faces, 20 edges and 15 vertices?
Solution: Here, F = 10, E = 20 and V = 15
We have:
F + V – E = 2
∴ 10 + 15 – 20 = 2
or 25 – 20 = 2
or 5 = 2 which is not true
i.e. F + V – E ≠ 2
Thus, such a polyhedron is not possible.





















