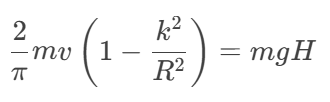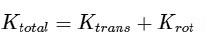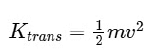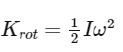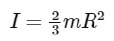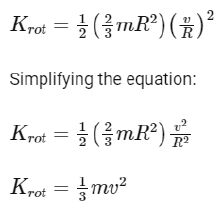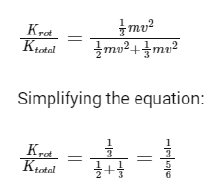Rolling Motion | Physics for JEE Main & Advanced PDF Download
| Table of contents |

|
| Introduction |

|
| What is Rolling Motion? |

|
| Concept of Rolling Motion |

|
| Kinetic Energy of Rolling Motion |

|
| Solved Examples |

|
| Difference Between Translational and Rotational Motion |

|
Introduction
Rolling motion is a fascinating phenomenon that combines both translational and rotational motion in a single movement. This type of motion is what we observe when an object, like a wheel or ball, moves along a surface while rotating around its own axis. Whether it's a car wheel gliding down the road or a ball rolling on the ground, rolling motion is all around us in everyday life.
What is Rolling Motion?
It is defined as the combined translational and rotational motion of an object. In rolling motion, an object moves along a surface while also rotating about its own axis. This type of motion is commonly observed in objects such as wheels, cylinders, or balls rolling on a surface.
 Motion of a Wheel
Motion of a Wheel
Concept of Rolling Motion
- Imagine a car driving on a straight road. If we observe one of its wheels while standing still, it appears to both spin and move forward.
- Now, think about the car having a special frame attached to it, moving at the same speed. In this frame, the wheel seems to only spin, and the car appears to just glide forward without any spinning.
- Consider a fan inside the car. When the car is parked, the fan only spins. However, when the car is in motion, the fan's movement is a combination of spinning and moving along with the car.
- If we are sitting inside the moving car, we see the fan spinning by itself, even though we understand that the car is also moving.
- This concept of separating movement into spinning and straight-line motion is very helpful for understanding how objects move.
- Looking at the motion of objects as a mix of rotational and translational motion is essentially studying rolling motion.
- When we analyze rolling motion, we assume that the center of mass moves in a straight line while the rest of the object rotates around this center of mass.
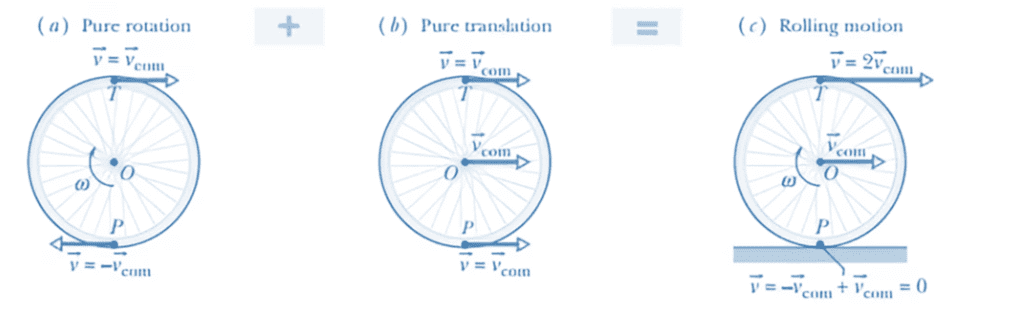 Rolling Motion
Rolling Motion
1. In the image (a), pure rotation is shown. Every point on the wheel rotates about the centre of mass with angular speed ω. And every point on the outside edge of the edge of the wheel has linear speed VCOM = ωR, where R is the radius of the wheel.
2. In the image (b), pure translation is shown. Every point on the outside edge of the wheel moves to the right with linear speed VCOM.
3. In the image (c), actual rolling motion is depicted.
Kinetic Energy of Rolling Motion
When a disc of radius R rolls over a smooth horizontal surface without slipping, it exhibits two types of motion:
- Linear motion: The centre of mass (COM) of the disc moves with a velocity (VCM) along the horizontal direction.
- Rotational motion: The disc rotates about a horizontal axis through its centre with an angular speed ω.
M → Mass of wheel
VCM → Velocity of the centre of mass
Linear kinetic energy of the centre of mass, KT= 1/2 MV2CM
"I" → Moment of inertia
"ω" Angular velocity
Rotational kinetic energy, KR= ½ Iω2
When a system of particles exhibits simultaneous translational and rotational motion the kinetic energy of a system of particles, KE, can be written as the sum of the kinetic energy due to translation, and kinetic energy due to rotation:
KE = KT + KR = ½ MV2CM + ½ Iω2
VCM=Rω so ω=VCM/R and I= Mk2, where k is the radius of gyration of the body
Putting the value of ω and I in the formula of kinetic energy we get,
KE= ½ MV2CM + ½ Mk2(VCM/R)2
KE= ½ MV2CM [1+(k2/R2)]
So, if we know the moment of inertia or radius of gyration of a body, then we can calculate the kinetic energy of that object.
Special Cases:
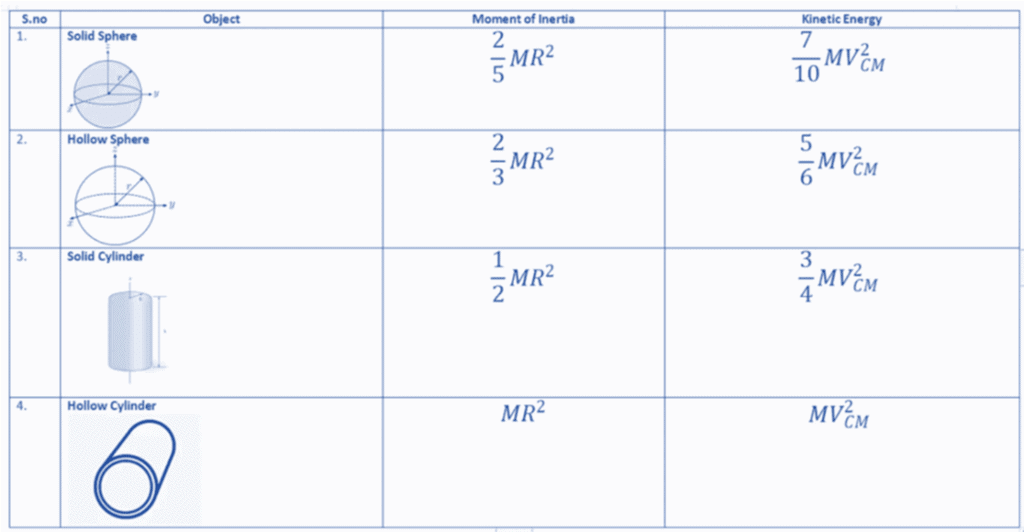
Solved Examples
Q1: A thin spherical shell of mass m and radius R rolls down a parabolic path PQR from a height H without slipping. Part PQ is suffciently rough while part QR is smooth. If the height reached by the shell on the part QR be h, then h/H is given by (assume R≪H)
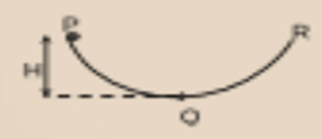
Ans: 3/5 H
Explanation: For pure rolling on part PQ, mechanical energy is conserved. Hence
For part QR, the translational Kinetic Energy = 1/2 mv2will be converted into potential energy. Hence 1/2 mv2=mgh. Hence h = 3/5 H
Q2: For a rolling spherical shell, the ratio of rotational kinetic energy and total kinetic energy is x/5. The value of X is ___________.
Ans: 2
Explanation: For a rolling spherical shell, we must consider the fact that it has both translational and rotational kinetic energy. The total kinetic energy (Ktotal) can be expressed as the sum of the translational kinetic energy ( Ktrans) and the rotational kinetic energy (Krot).
The translational kinetic energy of an object with mass (m) and linear velocity (v) is given by:
The rotational kinetic energy of a rolling spherical shell with moment of inertia (I) and angular velocity (ω) is given by:
For a rolling object without slipping, the relationship between linear velocity (v) and angular velocity (ω) is:
v = RωWhere R is the radius of the spherical shell.
The moment of inertia for a spherical shell is given by:
Now, we can substitute the moment of inertia and the relationship between linear and angular velocity into the equation for rotational kinetic energy:
Now, we can find the ratio of rotational kinetic energy to total kinetic energy:
Multiplying both the numerator and the denominator by 6:
Comparing this to the given ratio of x/5, we can determine that the value of x is 2.
Difference Between Translational and Rotational Motion
The table provides a comparative analysis of translational and rotational motion, which helps in understanding the fundamental aspects of both types of motion, which are essential concepts in physics.
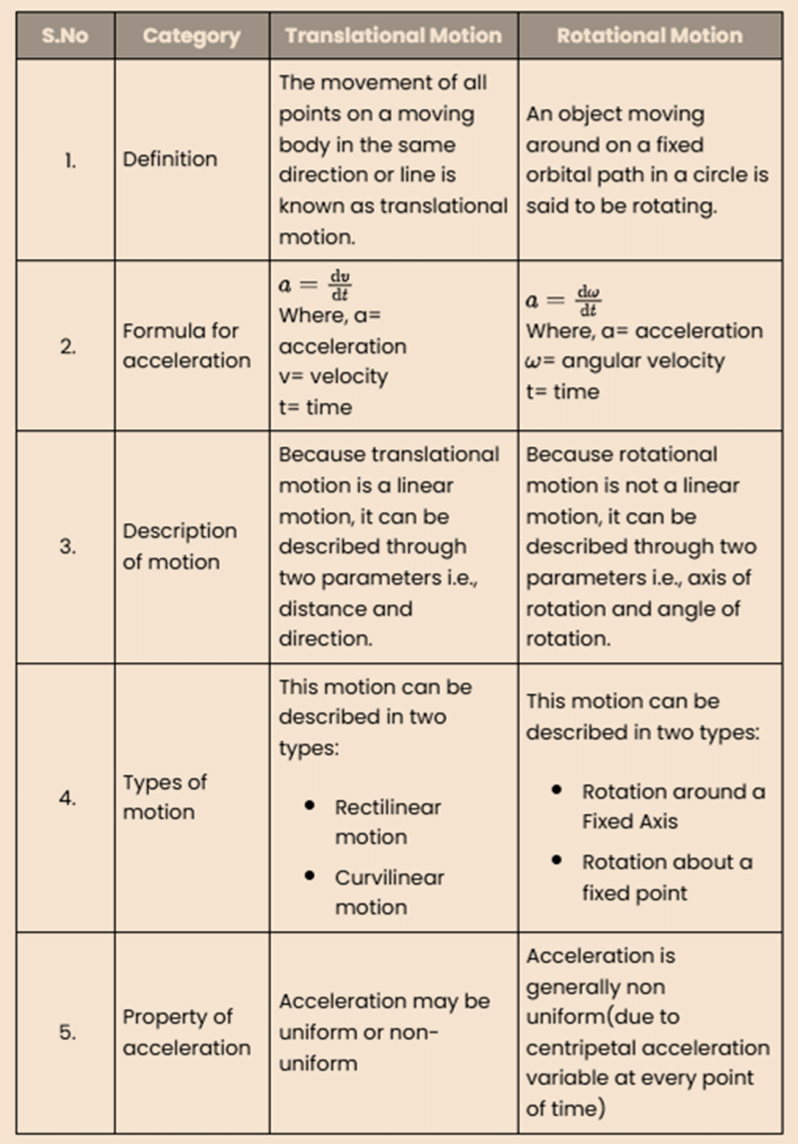
|
297 videos|948 docs|172 tests
|
FAQs on Rolling Motion - Physics for JEE Main & Advanced
| 1. What is rolling motion and how does it differ from sliding motion? |  |
| 2. How is the kinetic energy of an object in rolling motion calculated? |  |
| 3. What is the moment of inertia, and why is it important in rolling motion? |  |
| 4. Can rolling motion occur without slipping? If so, how? |  |
| 5. What are some real-life examples of rolling motion? |  |