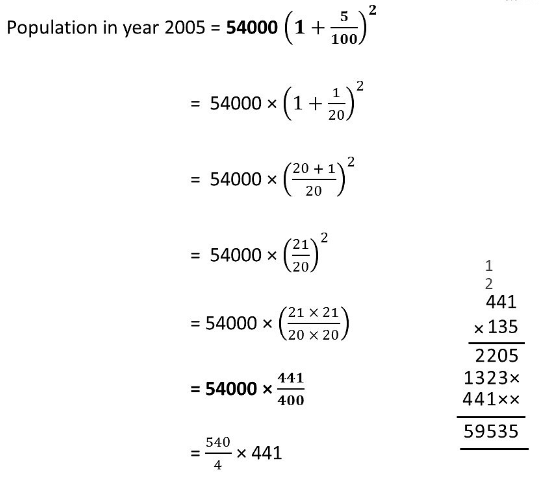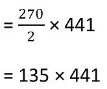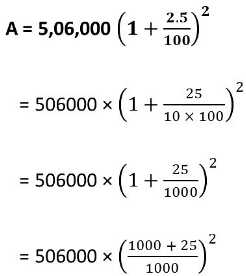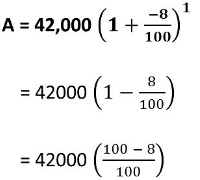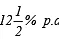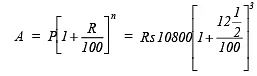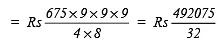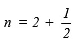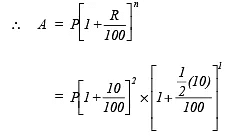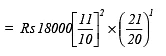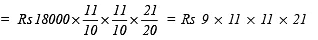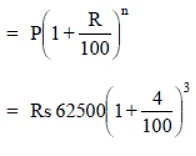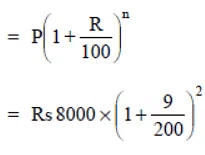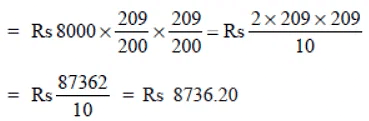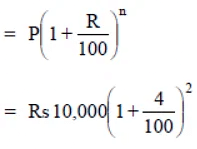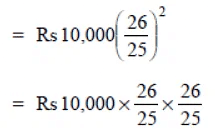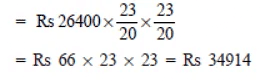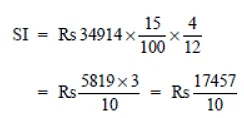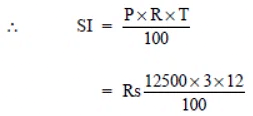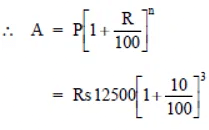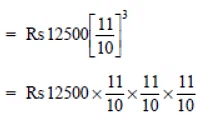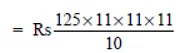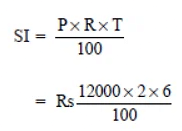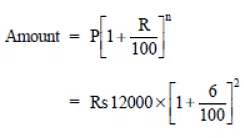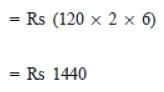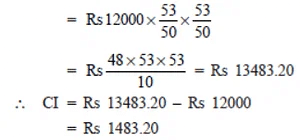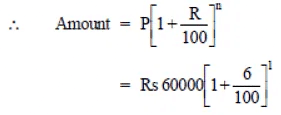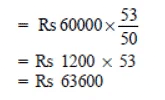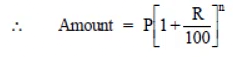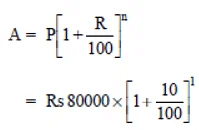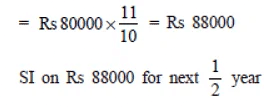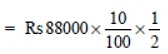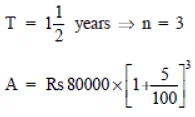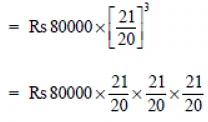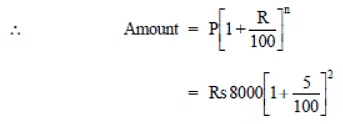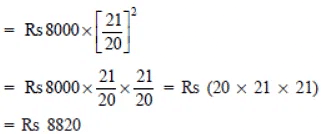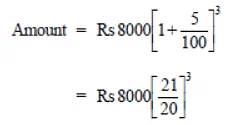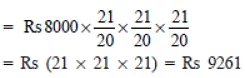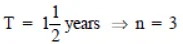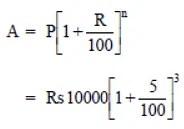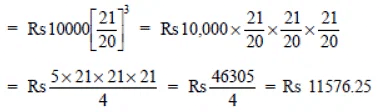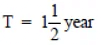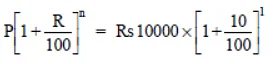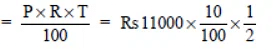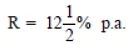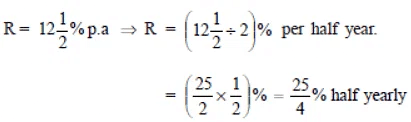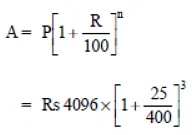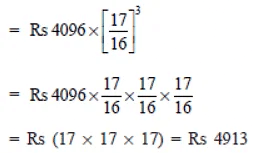NCERT Solutions for Class 8 Maths - Comparing Quantities - 3 (Exercise: 7.3)
Exercise: 7.3
Q1: The population of a place increased to 54,000 in 2003 at a rate of 5% per annum.
(i) Find the population in 2001.
(ii) What would be its population is 2005?
Sol: Population in 2003 is P = 54000
(i) Let the population in 2001 (i.e. 2 years ago) = P
Since rate of increment in population = 5% p.a.
∴ Present populationThus, the population in 2001 was about 48980.
(ii) Initial population (in 2003), i.e. P = 54000
Rate of increment in population = 5% p.a.
Time = 2 years ⇒n = 2
= 59535
Thus, the population in 2005 = 59,535.
Q2: In a laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000.
Sol: Initial count of bacteria (P) = 5,06,000
Increasing rate (R) = 2.5% per hour
Time (T) = 2 hour. ⇒ n = 2= 531616.25 or 531616 (approx.)
Thus, the count of bacteria after 2 hours will be 531616 (approx.).
Q3: A scooter was bought at ₹ 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.
Sol: Initial cost (value) of the scooter (P) = Rs 42000
Depreciation rate = 8% p.a.
Time = 1 year ⇒ n = 1
= ₹ 420 × 92 = ₹ 38,640
Thus, the value of the scooter after 1 year will be ₹ 38,640.
Try These
Q1: Machinery worth Rs 10,500 depreciated by 5%. Find its value after one year.
Ans: Here, P = Rs 10,500, R = –5% p.a., T = 1 year, n = 1
∵[∵ Depreciation is there, ∴ r = –5%]
∴
= Rs10500 * 19/20 = Rs 525 * 19 = Rs 9975
Thus, machinery value after 1 year = Rs 9975
Q2: Find the population of a city after 2 years, which is at present 12 lakh, if the rate of increase is 4%
Ans: Present population, P = 12 lakh
Rate of increase, R = 4% p.a.
Time, T = 2 years
∴ Population after 2 years =
Thus, the population of the town will be 12,97,920 after 2 years.
Note: For depreciation, we use the formula as
Old NCERT Questions
Try These
Q1: Find CI on a sum of Rs 8000 for 2 years at 5% per annum compounded annually. Solution: We have P = Rs 8000, R = 5% p.a., T = 2 years
Sol:
∵
∴
= Rs (20 * 21 * 21) = Rs 8820
Now, compound interest = A – P
= Rs 8820 – Rs 8000
= Rs 820
Remember
- The time period after which the interest is added each time to form a new principal is called the conversion period.
- If the interest is compounded half yearly, the time period becomes twice and rate becomes half of the annual rate.
- If the interest compounded quarterly, the time period becomes 4 times and rate become one-fourth of the annual rate.
- If the conversion period is not specified, then it is taken as one year and the interest is compounded annually.
Q2: Find the time period and rate for each.
- A sum taken for
years at 8% per annum is compounded half yearly.
- A sum taken for 2 years at 4% per annum compounded half yearly.
Sol:
1. We have an interest rate 8% per annum for
year.
∴ Time period
half years
Rate (R) = 1/2 (8%) = 4% per half year.
2. We have interest rate 4% per annum for 2 years.
∴ Time period (n) = 2(2) = 4 half years
Rate (R) = 1/2 (4%)= 2% per half year.
Q3: Find the amount to be paid
- At the end of 2 years on Rs 2,400 at 5% per annum compounded annually.
- At the end of 1 year on Rs 1,800 at 8% per annum compounded quarterly.
Sol:
1. We have: P = Rs 2400, R = 5% p.a., T = 2 years
∵ Interest is compounded annually i.e. n = 2
∴
2. Here, interest compounded quarterly.
∴ R = 8% p.a. = 8/4% i.e. 2% per quarter
T = 1 year = 4 * 1, i.e. 4 quarters or n = 4
Now
Q4: Calculate the amount and compound interest on
(a) Rs 10,800 for 3 years at 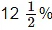 per annum compounded annually.
per annum compounded annually.
(b) Rs 18,000 for 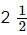 years at 10% per annum compounded annually.
years at 10% per annum compounded annually.
(c) Rs 62,500 for 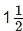 years at 8% per annum compounded half yearly.
years at 8% per annum compounded half yearly.
(d) Rs 8,000 for 1 year at 9% per annum compounded half yearly.
(You could use the year by year calculation using SI formula to verify.)
(e) Rs 10,000 for 1 year at 8% per annum compounded half yearly.
Sol: (a ) Here P = Rs 10800, T = 3 years, R =
We have:
[∵ Interest compounded annually,∴ n = 3]
∴ Amount = Rs 15377.34Rs 15377.34
Now, compound interest = Rs 15377.34 – Rs 10800
= Rs 4577.34
(b) Here P = Rs 18000, T =
years, R = 10% p.a.
∵ Interest is compounded annually,
= Rs 22869
∴ Amount = Rs 22869
CI = Rs 22869 – Rs 18000 = Rs 4869
(c) Here P = Rs 62500, T =
r = 8% p.a.
Compounding half yearly,
R = 8% p.a. = 4% per half year
T =
year → n = 3 half years.
∴ Amount
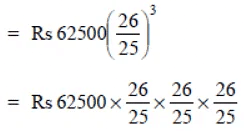
= Rs 4 * 26 * 26 * 26 = Rs 70304
Amount = RS 70304
CI = Rs 70304 – Rs 62500 = Rs 7804
(d) Here P = Rs 8000, T = 1 year, R = 9% p.a.
Interest is compounded half yearly,
∴ T = 1 year = 2 half years
R = 9% p.a = 9/2% half yearly
∴ Amount =
CI = Rs 8736.20 – Rs 8000
= Rs 736.20
(e) Here P = Rs 10000, T = 1 year
R = 8% p.a. compounded half yearly.
∴ R = 8% p.a. = 4% per half yearly
T = 1 year → n = 2 * 1 = 2
Now, amount
= Rs 16 * 26 * 26 = Rs 10816
CI = Rs 10816 – Rs 10000 = Rs 816
Q5: Kamala borrowed RS 26,400 from a Bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?
(Hint: Find A for 2 years with interest is compounded yearly and then find SI an the 2nd year for 4/12 years.)
Sol:
Note: Here, we shall calculate the amount for 2 years using the CI formula. Then this amount will become the principal for next 4 months, i.e. 4/12 years.
Here, P = Rs 26400, T = 2 years, R = 15% p.a
Again, P = 34914, T = 4 months = 4/12 years, R = 15% p.a.
∴ Using
we have
= Rs 1745.70
Amount = S.I. + P
= Rs (1745.70 + 34914) = Rs 36659.70
Thus, the required amount to be paid to the bank after 2 years 4 month = Rs 36659.70
Q6: Fabina borrows Rs 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much?
Sol:
For Fabina
P = Rs 12500
T = 3 years
R = 12% p.a.
= Rs 125 X 3 X 12
For Radha
P = Rs 12500
T = 3 years
R = 10% p.a. (Compounded annually)
= Rs 16637.5
∴ CI = 16637.5 – RS 12500 = 4137.50
Difference = Rs 4500 – Rs 4137.50 = Rs 362.50
Thus, Fabina pays Rs 362.50 more.
Q7: I borrowed Rs 12,000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?
Sol:
For SI
Principal = Rs 12000
Time = 2 years
Rate = 6% p.a.
For CI
Principal = Rs 12000
Time = 2 years
Rate = 6% p.a.
Thus, excess amount = Rs 1483.20 – Rs 1440
= Rs 43.20.
Q8: Vasudevan invested Rs 60,000 at an interest rate of 12% per annum compounded half yearly. What amount would he get
(i) after 6 months? (ii) after 1 year?
Sol:
(i) Amount after 6 months
P = Rs 60000
T = 1/2 year , n = 1 [∵ Interest is compounded half yearly.]
R = 12% p.a. = 6% per half year
(ii) Amount after 1 year
P = Rs 60000
T = 1 year; n = 2
R = 12% p.a. = 6% per half year
Thus, amount after 6 months = Rs 63600
and amount after 1 year = Rs 67416
Q9: Arif took a loan of Rs 80,000 from a bank. If the rate of interest is 10% per annum,find the difference in amounts he would be paying after 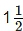 years if the interest is (i) Compounded annually. (ii) Compounded half yearly.
years if the interest is (i) Compounded annually. (ii) Compounded half yearly.
Sol:
(i) Compounded annually
P = Rs 80000
R = 10% p.a.
Amount for 1st year.
= Rs 440 *10 = Rs 4400
∴ Amount = Rs 88000 + Rs 44000
= Rs 92400
(ii) Compounded half yearly
P = Rs 80000
R = 10% p.a. = 5% per half year
= Rs 10 * 21 * 21 * 21
= Rs 92610
Thus, the difference between the two amounts = Rs 92610 – Rs 92400
= Rs 210
Q10: Maria invested Rs 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find:
(i) The amount credited against her name at the end of the second year.
(ii) The interest for the 3rd year.
Sol: Principal = Rs 8000
Rate = 5% p.a. compounded annually
(i) Time = 2 years ⇒ n = 2
∴ Amount credited against her name at the end of two years = Rs 8820
(ii) Time = 3 years ⇒ n = 3
∴
= Rs (21 * 21 * 21) = Rs 9261
∵ Interest paid during 3rd year
= [Amount at the end of 3rd year] – [Amount at the end of 2nd year]
= Rs 9261 – Rs 8820 = Rs 441
Q11: Find the amount and the compound interest on Rs 10,000 for 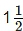 years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually?
years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually?
Sol:
Principal = Rs 10,000
Time =
%
Rate = 10% p.a.
Case I. Interest on compounded half yearly
We have r = 10 p.a. = 5% per half yearly
∴
∴ Amount = Rs 11576.25
Now CI = Amount – Principal
= Rs 11576.25 – Rs 10,000 = Rs 1576.25
Case II. Interest on compounded annually
We have R = 10% p.a.
Amount for 1 year =
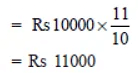
∴ Interest for 1st year = Rs 11000 – Rs 10,000 = Rs 1000
Interest for next 1/2 year on Rs 11000
= Rs 55 * 10 = Rs 550
∴ Total interest = Rs 1000 + Rs 550
= Rs 1550
Since Rs 1576.25 > Rs 1550
∴ Interest would be more in case of it is compounded half yearly.
Q12: Find the amount which Ram will get on Rs 4096, if he gave it for 18 months at 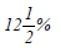 per annum, interest being compounded half yearly.
per annum, interest being compounded half yearly.
Sol:
We have P = Rs 4096
T = 18 months
∵ Interest is compounded half yearly.
T = 18 months ⇒ n = 18/6 = 3 six months
Now,
Thus, the required amount = Rs 4913
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 8 Maths - Comparing Quantities - 3 (Exercise: 7.3)
| 1. What are the key concepts covered in Exercise 7.3 of Comparing Quantities in Old NCERT? |  |
| 2. How can I solve problems related to percentage increase and decrease in Exercise 7.3? |  |
| 3. Are there any specific formulas to remember for solving questions in Comparing Quantities? |  |
| 4. How can I practice effectively for the Comparing Quantities chapter? |  |
| 5. What are the common mistakes to avoid while solving Exercise 7.3 questions? |  |