Chapter 17 - Understanding Shapes-III (Part - 1), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 17.9:
Question 1:
Given below is a parallelogram ABCD. Complete each statement along with the definition or property used.
(i) AD =
(ii) ∠DCB =
(iii) OC =
(iv) ∠DAB + ∠CDA =
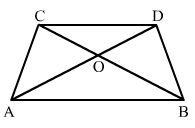
ANSWER:
The correct figure is
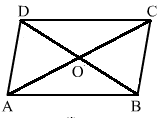
(i) AD = BC (opposite sides of a parallelogram are equal)
(ii) ∠DCB = ∠BAD (opposite angles are equal)
(iii) OC = OA (diagonals of a prallelogram bisect each other)
(iv) ∠DAB + ∠CDA = 180° (the sum of two adjacent angles of a parallelogram is 180°)
Question 2:
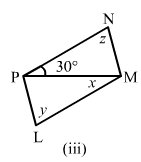
The following figures are parallelograms. Find the degree values of the unknowns x, y, z.
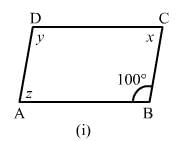
ANSWER:
(i) Opposite angles of a parallelogram are same.∴ x = z and y = 100°
Also, y + z = 180° (sum of adjacent angles of a quadrilateral is 180°)
z + 100° = 180°x
= 180°−100°x = 80°
∴ x = 80°, y = 100° and z = 80°
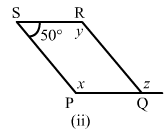
(ii) Opposite angles of a parallelogram are same.
∴ x = y and ∠RQP = 100°∠PSR + ∠SRQ
= 180°y + 50°
= 180°x = 180°−50°x
= 130°
∴ x = 130°, y = 130°
Since y and z are alternate angles, z = 130°
(iii) Sum of all angles in a triangle is 180∘.
∴30° + 90° + z = 180°
z = 60°
Opposite angles are equal in parallelogram.
∴ y = z = 60°and x = 30° (alternate angles)
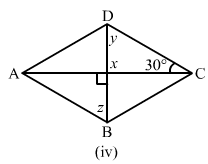
(iv) x = 90° (vertically opposite angle)
Sum of all angles in a triangle is 180∘.
∴ y + 90° + 30° = 180°
y = 180°−(90° + 30°) = 60°
y = z = 60° (alternate angles)
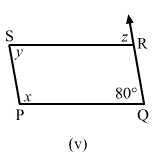
(v) Opposite angles are equal in a parallelogram.
∴ y = 80°y + x = 180°
x = 180°−100° = 80°
z = y = 80° (alternate angles)
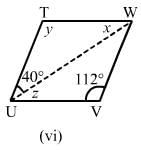
(vi) y = 112° (opposite angles are equal in a parallelogram)
InΔ UTW :x + y + 40° = 180° (angle sum property of a triangle)
x = 180°−(112°−40°) = 28°
Bottom left vertex = 180°−112° = 68°
∴ z = x = 28° (alternate angles)
PAGE NO 17.10:
Question 3:
Can the following figures be parallelograms. Justify your answer.
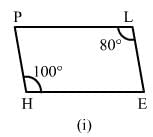
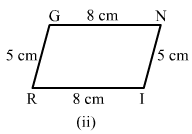
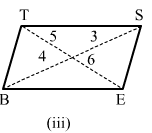
ANSWER:
(i) No. This is because the opposite angles are not equal.
(ii) Yes. This is because the opposite sides are equal.
(ii) No, This is because the diagonals do not bisect each other.
Question 4:
In the adjacent figure HOPE is a parallelogram. Find the angle measures x,y and z. State the geometrical truths you use to find them.
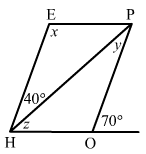
ANSWER:
∠HOP + 70° = 180° (linear pair)
∠HOP = 180°−70° = 110°
x = ∠HOP = 110° (opposite angles of a parallelogram are equal)
∠EHP + ∠HEP = 180° (sum of adjacent angles of a parallelogram is 180°)
110° + 40° + z = 180°
z = 180°−150° = 30°
y = 40° (alternate angles )
Question 5:
In the following figures GUNS and RUNS are parallelograms. Find x and y.
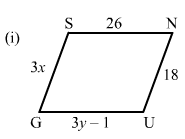
ANSWER:
(i) Opposite sides are equal in a parallelogram.
∴ 3y−1 = 26
3y = 27
y = 9
Similarly, 3x = 18x = 6
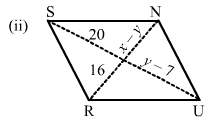
(ii) Diagonals bisect each other in a parallelogram.
∴ y−7 = 20
y = 27
x−y = 16
x−27 = 16
x = 43
Question 6:
In the following figure RISK and CLUE are parallelograms. Find the measure of x.
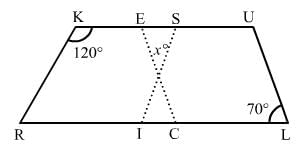
ANSWER:
In the parallelogram RISK:
∠ISK + ∠RKS = 180° (sum of adjacent angles of a parallelogram is 180°)
∠ISK = 180°−120° = 60°
Similarly, in parallelogram CLUE:
∠CEU = ∠CLU = 70° (opposite angles of a parallelogram are equal)
In the triangle:
x + ∠ISK + ∠CEU = 180°
x = 180°−(70° + 60°)
x = 180°−(70° + 60°)
= 50°
Question 7:
Two opposite angles of a parallelogram are (3x − 2)° and (50 − x)°. Find the measure of each angle of the parallelogram.
ANSWER:
Opposite angles of a parallelogram are congruent.
∴ (3x−2)° = (50−x)°
3x°−2° = 50°−x°
3x° + x° = 50° + 2°
4x° = 52°
x° = 13°
Putting the value of x in one angle: 3x°−2° = 39°−2° = 37°
Opposite angles are congruent:
∴ 50−x° = 37°
Let the remaining two angles be y and z.
Angles y and z are congruent because they are also opposite angles.
∴ y = z
The sum of adjacent angles of a parallelogram is equal to 180°.
∴37° + y = 180°
y = 180°−37°
y = 143°
So, the angles measure are:37°, 37°, 143° and 143°
Question 8:
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram.
ANSWER:
Two adjacent angles of a parallelogram add up to 180°.
Let x be the angle.
∴ x + 2x/3 = 180°
5x/3 = = 180°
x = 72°
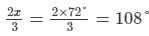
Thus, two of the angles in the parallelogram are 108° and the other two are 72°.
Question 9:
The measure of one angle of a parallelogram is 70°. What are the measures of the remaining angles?
ANSWER:
Given that one angle of the parallelogram is 70°.
Since opposite angles have same value, if one is 70°,
then the one directly opposite will also be 70°.
So, let one angle be x°.x° + 70° = 180° (the sum of adjacent angles of a parallelogram is 180° )
x° = 180°−70°
x° = 110°
Thus, the remaining angles are 110°, 110° and 70°.
Question 10:
Two adjacent angles of a parallelogram are as 1 : 2. Find the measures of all the angles of the parallelogram.
ANSWER:
Let the angle be A and B.The angles are in the ratio of 1:2.
Measures of ∠A and ∠B are x° and 2x°.
Then, ∠C = ∠A
and ∠D = ∠B (opposite angles of a parallelogram are congruent) As we know that the sum of adjacent angles of a parallelogram is 180°.
∴ ∠A + ∠B = 180°
⇒ x° + 2x° = 180°
⇒ 3x° = 180°
⇒ x° = 180°/3 = 60°
Thus, measure of ∠A = 60°, ∠B = 120°, ∠C = 60°
and ∠D = 120°.
Question 11:
In a parallelogram ABCD, ∠D = 135°, determine the measure of ∠A and ∠B.
ANSWER:
In a parallelogram, opposite angles have the same value.
∴ ∠D = ∠B = 135°
Also, ∠A + ∠B + ∠C + ∠D = 360°
∠A + ∠D = 180° (opposite angles have the same value)
∠A = 180°−135° = 45°
∠A = 45°
PAGE NO 17.11:
Question 12:
ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D.
ANSWER:
Opposite angles of a parallelogram are equal.
∴ ∠C = 70° = ∠A.
∠B = ∠D
Also, the sum of the adjacent angles of a parallelogram is 180°.
∴ ∠A + ∠B = 180°
70° + ∠B = 180°
∠B = 110°
∴ ∠B = 110°, ∠C = 70° and ∠D = 110°
Question 13:
The sum of two opposite angles of a parallelogram is 130°. Find all the angles of the parallelogram.
ANSWER:
Let the angles be A, B, C and D.It is given that the sum of two opposite angles is 130°.
∴ ∠A + ∠C = 130°
∠A + ∠A = 130° (opposite angles of a parallelogram are same)
∠A = 65°and ∠C = 65°
The sum of adjacent angles of a parallelogram is 180°.
∠A + ∠B = 180°
65° + ∠B = 180°
∠B = 180°−65°
∠B = 115°
∠D = 115°
∴ ∠A = 65°, v∠B = 115°, ∠C = 65° and ∠D = 115°.
Question 14:
All the angles of a quadrilateral are equal to each other. Find the measure of each. Is the quadrilateral a parallelogram? What special type of parallelogram is it?
ANSWER:
Let the angle be x.
All the angles are equal.
∴ x + x + x + x = 360°
4x = 360°
x = 90°
So, each angle is 90° and quadrilateral is a parallelogram. It is a rectangle.
Question 15:
Two adjacent sides of a parallelogram are 4 cm and 3 cm respectively. Find its perimeter.
ANSWER:
We know that the opposite sides of a parallelogram are equal.
Two sides are given, i.e. 4 cm and 3 cm.
Therefore, the rest of the sies will also be 4 cm and 3 cm.
∴ Perimeter = Sum of all the sides of a parallelogram = 4 + 3 + 4 + 3 = 14 cm
Question 16:
The perimeter of a parallelogram is 150 cm. One of its sides is greater than the other by 25 cm. Find the length of the sides of the parallelogram.
ANSWER:
Opposite sides of a parallelogram are same.
Let two sides of the parallelogram be x and y.
Given: x = y + 25
Also, x + y + x + y = 150 (Perimeter = Sum of all the sides of a parallelogram)
y + 25 + y + y + 25 + y = 150
4y = 150−50
4y = 100
y = 100/4 = 25
∴ x = y + 25 = 25 + 25 = 50
Thus, the lengths of the sides of the parallelogram are 50 cm and 25 cm.
Question 17:
The shorter side of a parallelogram is 4.8 cm and the longer side is half as much again as the shorter side. Find the perimeter of the parallelogram.
ANSWER:
Given:Shorter side = 4.8 cm
Longer side = 4.8/22 + 4.8 = 7.2 cm
Perimeter = Sum of all the sides = 4.8 + 4.8 + 7.2 + 7.2
= 24 cm
Question 18:
Two adjacent angles of a parallelogram are (3x − 4)° and (3x + 10)°. Find the angles of the parallelogram.
ANSWER:
We know that the adjacent angles of a parallelogram are supplementry.
Hence, (3x + 10)° and (3x−4)° are supplementry.(3x + 10)° + (3x−4)° = 180°
6x° + 6° = 180°
6x° = 174°
x = 29°
First angle = (3x + 10)° = (3×29° + 10°) = 97°
Second angle = (3x−4)° = 83°
Thus, the angles of the parallelogram are 97°, 83°, 97° and 83°.
Question 19:
In a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC = 30°, ∠BDC = 10° and ∠CAB = 70°. Find:
∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB, ∠ACB, ∠DBC and ∠DBA.
ANSWER:
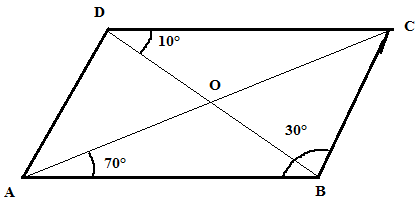
∠ABC = 30°
∴ ∠ADC = 30° (opposite angle of the parallelogram)
and ∠BDA = ∠ADC−∠BDC = 30°−10° = 20°
∠BAC = ∠ACD = 70° (alternate angle)
In △ ABC:∠CAB + ∠ABC + ∠BCA
= 180°70° + 30° + ∠BCA = 180°
∴ ∠BCA = 80°
∠DAB = ∠DAC + ∠CAB
= 70° + 80° = 150°
∠BCD = 150° (opposite angle of the parallelogram)
∠DCA = ∠CAB = 70°
In △DOC:∠ODC + ∠DOC + ∠OCD = 180
10° + 70° + ∠DOC = 180°
∴∠DOC = 100°
∠DOC + ∠BOC = 180°
∠BOC = 180°−100°
∠BOC = 80°
∠AOD = ∠BOC = 80° (vertically opposite angles)
∠AOB = ∠DOC = 100° (vertically opposite angles)
∠CAB = 70° (given)
∠ADB = 20°
∠DBA = ∠BDC = 10° (alternate angle)
∠ADB = ∠DBC = 20° (alternate angle)
Question 20:
Find the angles marked with a question mark shown in Fig. 17.27
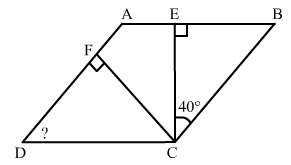
ANSWER:
In △CEB:∠ECB + ∠CBE + ∠BEC = 180° (angle sum property of a triangle)
40° + 90° + ∠EBC = 180°
∴ ∠EBC = 50°
Also, ∠EBC = ∠ADC = 50° (opposite angle of a parallelogram)
In △FDC:∠FDC + ∠DCF + ∠CFD
= 180°50° + 90° + ∠DCF = 180°
∴ ∠DCF = 40°
Now, ∠BCE + ∠ECF + ∠FCD + ∠FDC = 180° (in a parallelogram, the sum of alternate angles is 180° )
50° + 40° + ∠ECF + 40° = 180°
∠ECF = 180°−50° + 40°−40° = 50°
Question 21:
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60°. Find the angles of the parallelogram.
ANSWER:
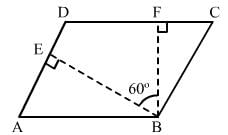
Draw a parallelogram ABCD.
Drop a perpendicular from B to the side AD, at the point E.
Drop perpendicular from B to the side CD, at the point F.
In the quadrilateral BEDF:
∠EBF = 60°,
∠BED = 90°
∠BFD = 90°
∠EDF = 360°−(60° + 90° + 90°) = 120°
In a parallelogram, opposite angles are congruent and adjacent angles are supplementary.
In the parallelogram ABCD: ∠B = ∠D = 120°
∠A = ∠C = 180°−120° = 60°
Question 22:
In Fig. 17.28, ABCD and AEFG are parallelograms. If ∠C = 55°, what is the measure of ∠F?
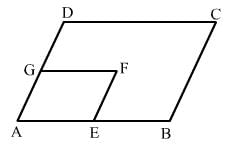
ANSWER:
Both the parallelograms ABCD and AEFG are similar.
∴ ∠C = ∠A = 55° (opposite angles of a parallelogram are equal)
∴ ∠A = ∠F = 55° (opposite angles of a parallelogram are equal)
Question 23:
In Fig. 17.29, BDEF and DCEF are each a parallelogram. Is it true that BD = DC? Why or why not?
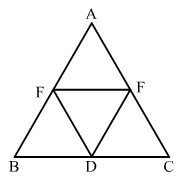
ANSWER:
In parallelogram BDEF
∴ BD = EF ...(i) (opposite sides of a parallelogram are equal)
In parallelogram DCEF CD = EF ...(ii) (opposite sides of a parallelogram are equal)
From equations (i) and (ii) BD = CD
PAGE NO 17.12:
Question 24:
In Fig. 17.29, suppose it is known that DE = DF. Then, is ΔABC isosceles? Why or why not?
Fig. 17.29
ANSWER:
In ΔFDE:DE = DF ∴ ∠FED = ∠DFE.............(i) (angles opposite to equal sides)
In the IIgm BDEF: ∠FBD = ∠FED.......(ii) (opposite angles of a parallelogram are equal)
In the IIgm DCEF:∠DCE = ∠DFE......(iii) (opposite angles of a parallelogram are equal)
From equations (i) , (ii) and (iii) :
∠FBD = ∠DCEIn
△ABC:If ∠FBD = ∠DCE, then AB = AC (sides opposite to equal angles) .
Hence, △ABC is isosceles.
Question 25:
Diagonals of parallelogram ABCD intersect at O as shown in Fig. 17.30. XY contains O, and X, Y are points on opposite sides of the parallelogram. Give reasons for each of the following:
(i) OB = OD
(ii) ∠OBY = ∠ODX
(iii) ∠BOY = ∠DOX
(iv) ∆BOY ≅ ∆DOX
Now, state if XY is bisected at O.
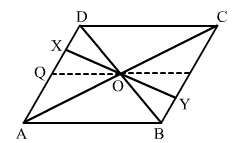
ANSWER:
(i) Diagonals of a parallelogram bisect each other.
(ii) Alternate angles
(iii) Vertically opposite angles
(iv)
In ΔBOY and ΔDOX:OB = OD (diagonals of a parallelogram bisect each other)
∠OBY = ∠ODX (alternate angles)
∠BOY = ∠DOX (vertically opposite angles)
In ∆BOY and ∆DOX:OB = OD (diagonals of a parallelogram bisect each other)
∠OBY = ∠ODX (alternate angles)
∠BOY = ∠DOX (vertically opposite angles)
ASA congruence:
XO = YO (c.p.c.t)
So, XY is bisected at O.
Question 26:
In Fig. 17.31, ABCD is a parallelogram, CE bisects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same:
(i) ∠A = ∠C
(ii) ∠FAB = 1/2∠A
(iii) ∠DCE = 1/2∠C
(iv) ∠CEB = ∠FAB
(v) CE || AF
ANSWER:
(i) True, since opposite angles of a parallelogram are equal.
(ii) True, as AF is the bisector of ∠A.
(iii) True, as CE is the bisector of ∠C.
(iv) True
∠CEB = ∠DCE........(i) (alternate angles)
∠DCE = ∠ FAB.........(ii) (opposite angles of a parallelogram are equal)
From equations (i) and (ii) :
∠CEB = ∠FAB
(v) True, as corresponding angles are equal (∠CEB = ∠FAB) .
Question 27:
Diagonals of a parallelogram ABCD intersect at O. AL and CM are drawn perpendiculars to BD such that L and M lie on BD. Is AL = CM? Why or why not?
ANSWER:
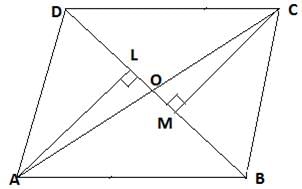
In ΔAOL and ΔCMO:∠AOL = ∠COM( vertically opposite angle) ....(i)
∠ALO = ∠CMO = 90° (each right angle) .....(ii)
Using angle sum property: ∠AOL + ∠ALO + ∠LAO = 180°..........(iii)
∠COM + ∠CMO + ∠OCM = 180°......(iv)
From equations (iii) and (iv) :∠AOL + ∠ALO + ∠LAO
= ∠COM + ∠CMO + ∠OCM
∠LAO = ∠OCM (from equations (i) and (ii))
In ΔAOL and ΔCMO:∠ALO = ∠CMO (each right angle)
AO = OC (diagonals of a parallelogram bisect each other)
∠LAO = ∠OCM (proved above)
So, ΔAOL is congruent to ΔCMO (SAS)
.⇒ AL = CM [cpct]
Question 28:
Points E and F lie on diagonal AC of a parallelogram ABCD such that AE = CF. What type of quadrilateral is BFDE?
ANSWER:
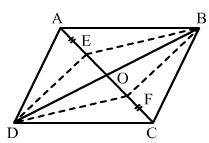
In the IIgm ABCD:
AO = OC......(i) (diagonals of a parallelogram bisect each other) AE = CF.......(ii) (given)
Subtracting (ii) from (i) :AO−AE = OC−CF
EO = OF......... (iii)
In ΔDOE and ΔBOF:
EO = OF (proved above)
DO = OB (diagonals of a parallelogram bisect each other) ∠DOE = ∠BOF (vertically opposite angles)
By SAS congruence: ΔDOE≅ ΔBOF
∴ DE = BF (c.p.c.t)
In ΔBOE and ΔDOF:
EO = OF (proved above)
DO = OB (diagonals of a parallelogram bisect each other)
∠DOF = ∠BOE (vertically opposite angles)
By SAS congruence: ΔDOE≅ ΔBOF
∴ DF = BE (c.p.c.t)
Hence, the pair of opposite sides are equal.
Thus, DEBF is a parallelogram.
Question 29:
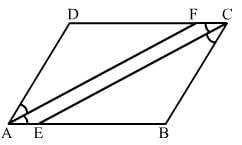
In a parallelogram ABCD, AB = 10 cm, AD = 6 cm. The bisector of ∠A meets DC in E, AE and BC produced meet at F. Find te length CF.
ANSWER:
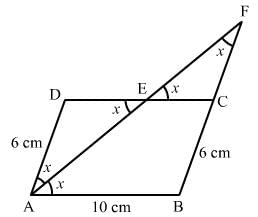
AE is the bisector of ∠A.
∴ ∠DAE = ∠BAE = x
∠BAE = ∠AED = x (alternate angles) Since opposite angles in ΔADE are equal, ΔADE is an isosceles triangle.
∴ AD = DE = 6 cm (sides opposite to equal angles)
AB = CD = 10 cm
CD = DE + EC
⇒ EC = CD−DE
⇒ EC = 10−6 = 4 cm
∠DEA = ∠CEF = x (vertically opposite angle)
∠EAD = ∠EFC = x (alternate angles)
Since opposite angles in ΔEFC are equal, ΔEFC is an isosceles triangle.
∴ CF = CE = 4 cm (sides opposite to equal angles)
∴ CF = 4cm
FAQs on Chapter 17 - Understanding Shapes-III (Part - 1), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What are the properties of a parallelogram? |  |
| 2. How do you find the area of a triangle? |  |
| 3. What is the difference between a rectangle and a square? |  |
| 4. What is the formula to calculate the perimeter of a polygon? |  |
| 5. How can you determine if a quadrilateral is a trapezium? |  |
















