Class 8 Maths Chapter 6 Question Answers - Cubes and Cube Roots
| Table of contents |

|
| Try These Questions (Page No. 73) |

|
| Think, Discuss and Write Questions(Page No. 74) |

|
| Think, Discuss and Write Questions (Page No. 75) |

|
| Think, Discuss and Write Questions (Page No. 77) |

|
Try These Questions (Page No. 73)
Q.1. Find the one’s digit of the cube of each of the following numbers.
(i) 3331
(ii) 8888
(iii) 149
(iv) 1005
(v) 1024
(vi) 77
(vii) 5022
(viii) 53
Solution.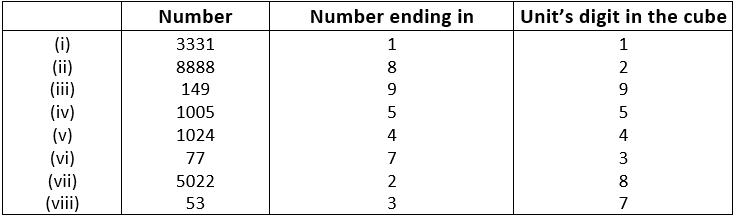
Note:
- There areonly 4 numbers, less than 100 which are perfect cubes.
They are: 1, 8, 27 and 64.- There areonly 5 numbers between 100 and 1000 which are perfect cubes.
These are: 125, 216, 343, 512 and 729.- The least 4 digit perfect cube is 1000.
Try These Questions (Page No. 73)
Q.1.Express the following numbers as the sum of odd numbers using the above pattern?
(a) 63
(b) 83
(c) 73
Solution.
(a)n = 6 and (n – 1) = 5
∴ We start with (6 * 5) + 1 = 31
We have:
63 = 31 + 33 + 35 + 37 + 39 + 41 = 216
(b)n = 8 and (n – 1) = 7
∴ We start with (8 * 7) + 1 = 57
We have:
83 = 57 + 59 + 61 + 63 + 65 + 67 + 69 + 71 = 512
(c)n = 7 and (n – 1) = 6
∴ We start with (7 * 6) + 1 = 43
we have:
73 = 43 + 45 + 47 + 49 + 51 + 53 + 55 = 343
Try These Questions (Page No. 73)
Q.1.Consider the following pattern:
23 – 13 = 1 + 2 * 1 * 3
33 – 23 = 1 + 3 * 2 * 3
43 – 33 = 1 + 4 * 3 * 3
Using the above pattern, find the value of the following.
(i) 73 – 63
(ii) 123 – 113
(iii) 203 – 193
(iv) 513 – 503
Solution.
(i) 73 – 63 = 1 + 7 * 6 * 3
= 1 + 126 = 127
(ii)123 – 113 = 1 + 12 * 11 * 3
= 1 + 396 = 397
(iii) 203 – 193 = 1 + 20 * 11 * 3
= 1 + 1140 = 1141
(iv) 513 – 503 = 1 + 51 * 50 * 3
= 1 + 7650 = 7651
Note:In the prime factorisation of any number, if each factor appears three times, then the number is a perfect cube.
Think, Discuss and Write Questions(Page No. 74)
Q.1. Which of the following are perfect cubes?
(i) 400
(ii) 3375
(iii) 8000
(iv) 15625
(v) 9000
(vi) 6859
(vii) 2025
(viii) 10648
Solution.
(i)
We have 400 = 2 * 2 * 2 * 2 * 5 * 5
∵ 2 * 5 * 5 remain after grouping in triples.
∴ 400 is not a perfect cube.
(ii)
We have 3375 = 3 * 3 * 3 * 5 * 5 * 5
∵ The prime factors appear in triples.
∴ 3375 is a perfect cube.
(iii)
We have 8000 = 2 * 2 * 2 * 2 * 2 * 2 * 5 * 5 * 5
∵ The prime factors of 8000 can be grouped into triples and no factor is left over.
∴ 8000 is a perfect cube.
(iv)
We have 15625 = 5 * 5 * 5 * 5 * 5 * 5
∵ The prime factors of 15625 can be grouped into triples and no factor is left over.
∴ 15625 is a perfect cube.
(v)
We have 9000 = 2 * 2 * 2 * 3 * 3 * 5 * 5 * 5
∵ The prime factors of 9000 cannot be grouped into triples (because 3 * 3 are left over).
∴ 9000 is not a perfect cube.
(vi)
We have 6859 = 19 * 19 * 19
∵ The prime factors of 6859 can be grouped into triples and no factor is left over.
∴ 6859 is a perfect cube.
(vii)
We have 2025 = 3 * 3 * 3 * 3 * 5 * 5
∵ We do not get triples of prime factors of 2025 and 3 * 5 * 5 are left over.
∴ 2025 is not a perfect cube.
(viii)
We have 10648 = 2 * 2 * 2 * 11 * 11 * 11
∵ The prime factors of 10648 can be grouped into triples and no factor is left over.
∴ 10648 is a perfect cube.
Think, Discuss and Write Questions (Page No. 75)
Q.1. Check which of the following are perfect cubes.(i) 2700
(ii) 16000
(iii) 64000
(iv) 900
(v) 125000
(vi) 36000
(vii) 21600
(viii) 10000
(ix) 27000000
(x) 1000
What pattern do you observe in these perfect cubes?
Solution.
(i)
We have 2700 = 2 * 2 * 3 * 3 * 3 * 5 * 5
We do not get complete triples of prime factors, i.e. 2 * 2 and 5 * 5 are left over.
∴ 2700 is not a perfect cube.
(ii)
We have 1600 = 2 * 2 * 2 * 2 * 2 * 2 * 5 * 5
After grouping is 3’s we get 5 * 5 which is ungrouped in triples.
∴ 1600 is not a perfect cube.
(iii)
We have 64000 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 5 * 5 * 5
Since we get groups of triples.
∴ 64000 is a perfect cube.
(iv)
We have 900 = 2 * 2 * 3 * 3 * 5 * 5
which are ungrouped in triples.
∴ 900 is not a perfect cube.
(v)
We have 125000 = 2 * 2 * 2 * 5 * 5 * 5 * 5 * 5 * 5
As we get all the prime factors in the group of triples.
∴ 125000 is a perfect cube.
(vi)
We have 36000 = 2 * 2 * 2 * 2 * 2 * 3 * 3 * 5 * 5 * 5
While grouping the prime factors of 36000 in triples, we are left over with 2 * 2 and 3 * 3.
∴ 36000 is not a perfect cube.
(vii)
We have 21600 = 2 * 2 * 2 * 2 * 2 * 3 * 3 * 3 * 5 * 5
While grouping the prime factors of 21600 in triples, we are left with 2 * 2 and 5 * 5.
∴ 21600 is not a perfect cube.
(viii)
We have 10000 = 2 * 2 * 2 * 2 * 5 * 5 * 5 * 5
While grouping the prime factors into triples, we are left over with 2 and 5.
∴ 10000 is not a perfect cube.
(ix)
We have 27000000 = 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 3 * 5 * 5 * 5 * 5 * 5 * 5
Since all the prime factors of 27000000 appear in groups of triples.
∴ 27000000 is a perfect cube.
(x)
We have 1000 = 2 * 2 * 2 * 5 * 5 * 5
Since all the prime factors of 1000 appear in groups of triples.
∴ 1000 is a perfect cube.
Now, in these perfect cubes, we can say that “the number of zeros at the end of a perfect cube must be 3 or a multiple of 3, failing which the number cannot be a perfect cube.”
Think, Discuss and Write Questions (Page No. 77)
Think, Discuss and Write Questions (Page No. 77)
Q.5.Statetrue or false: for any integer m, m2 < m3. Why?
Solution.
This inequality m2 < m3 is not true for all integers m.
Let's analyze different cases:
For m = 0:
m2 = 02 = 0,
m3 = 03 = 0
⟹m2 ≮ m3Hence, the inequality does not hold.
For m = 1:
m2 = 12 = 1
m3 = 13 = 1
⟹m2 ≮ m3Again, the inequality fails.
For m = −1:
m2 = (−1)2 = 1
m3=(−1)3=−1
⟹m2 > m3Thus, the inequality is false in this case as well.
For m > 1:
m2 < m3The inequality holds for m > 1, since m3 = m2
m > m2 when m > 1.For m < −1:
m2 > m3For negative integers less than −1, m2 is positive (since squaring makes the result positive), and m3 is negative (since the cube of a negative number remains negative). Hence, m2>m3.
Therefore, The inequality m2 < m3 is not true for all integers m, so the statement is false. It only holds for integers m > 1.
|
81 videos|452 docs|31 tests
|
FAQs on Class 8 Maths Chapter 6 Question Answers - Cubes and Cube Roots
| 1. What is a cube and how is it different from a square? |  |
| 2. How do you find the cube of a number? |  |
| 3. What is a cube root and how is it calculated? |  |
| 4. What is the relationship between cubes and cube roots? |  |
| 5. How can cubes and cube roots be applied in real-life situations? |  |





















