Bank Exams Exam > Bank Exams Notes > NCERT Mathematics for Competitive Exams > Exercise 4.4 NCERT Solutions - Linear Equations in Two Variables
NCERT Solutions for Class 9 Maths Chapter 4 - Exercise 4.4 Linear Equations in Two Variables
Page: 77
Q.1. Give the geometric representations of y = 3 as an equation
(i) in one variable
(ii) in two variables
Solution:
- In one variable, y = 3
 (ii) In two variable, 0x + y = 3
(ii) In two variable, 0x + y = 3
When x = 0, y = 3
When x = 1, y = 3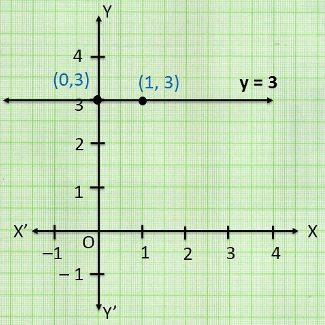
Q.2. Give the geometric representations of 2x + 9 = 0 as an equation
(i) in one variable
(ii) in two variables
Solution:
(i) In one variable,
2x + 9 = 0
2x = -9
x = -9/2
x = -4.5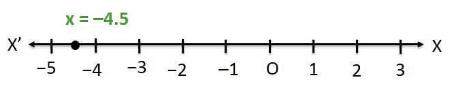 (ii) In two variables,
(ii) In two variables,
2x + 9 = 0
2x + 0y + 9 = 0
When y = 0, x = -4.5
When y = 1, x = -4.5
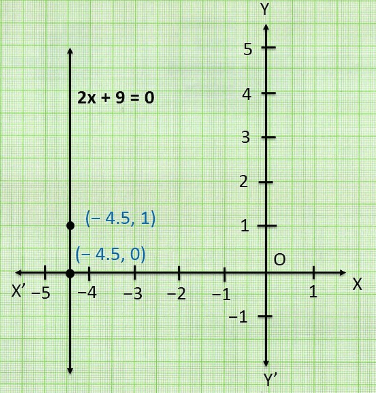
The document NCERT Solutions for Class 9 Maths Chapter 4 - Exercise 4.4 Linear Equations in Two Variables is a part of the Bank Exams Course NCERT Mathematics for Competitive Exams.
All you need of Bank Exams at this link: Bank Exams
|
276 docs|155 tests
|
FAQs on NCERT Solutions for Class 9 Maths Chapter 4 - Exercise 4.4 Linear Equations in Two Variables
| 1. What is a linear equation in two variables? |  |
Ans. A linear equation in two variables is an equation that can be expressed in the form ax + by = c, where a, b, and c are constants, and x and y are variables. It represents a straight line on a coordinate plane.
| 2. How can we solve a linear equation in two variables graphically? |  |
Ans. To solve a linear equation in two variables graphically, we plot the given equation on a coordinate plane and find the point of intersection between the line and the x-axis or y-axis. The coordinates of the intersection point represent the solution to the equation.
| 3. What is the method of substitution to solve a linear equation in two variables? |  |
Ans. The method of substitution is a technique used to solve a linear equation in two variables. In this method, we solve one equation for one variable and substitute this value into the other equation. By substituting the value and solving the resulting equation, we can find the values of both variables.
| 4. How can we solve a system of linear equations in two variables algebraically? |  |
Ans. To solve a system of linear equations in two variables algebraically, we can use the method of elimination or the method of substitution. In the method of elimination, we eliminate one variable by adding or subtracting the equations, while in the method of substitution, we substitute the value of one variable into the other equation.
| 5. What is the significance of solving linear equations in two variables? |  |
Ans. Solving linear equations in two variables is significant in many real-life applications, such as finding the point of intersection between two lines, determining the solution to a system of equations, and analyzing the relationship between two variables. It helps in solving problems related to economics, physics, engineering, and other fields.
Related Searches





















