Open App

Class 8 Exam > Class 8 Notes > RD Sharma Solutions for Class 8 Mathematics > RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math

Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download

QUESTION 7: BY WHAT NUMBER SHOULD EACH OF THE FOLLOWING NUMBERS BE MULTIPLIED TO GET A PERFECT SQUARE IN EACH CASE? ALSO, FIND THE NUMBER WHOSE SQUARE IS THE NEW NUMBER.
(I) 8820
(II) 3675
(III) 605
(IV) 2880
(V) 4056
(VI) 3468
(VII) 7776
ANSWER 7: Factorising each number.
(i) 8820 = 2 x 2 x 3 x 3 x 5 x 7 x 7

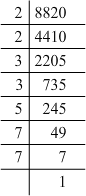
Grouping them into pairs of equal factors:
8820 = (2 x 2) x (3 x 3) x (7 x 7) x 5
The factor, 5 is not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 8820 must be multiplied by 5 for it to be a perfect square.
The new number would be (2 x 2) x (3 x 3) x (7 x 7) x (5 x 5).
Furthermore, we have:
(2 x 2) x (3 x 3) x (7 x 7) x (5 x 5) = (2 x 3 x 5 x 7) x (2 x 3 x 5 x 7)
Hence, the number whose square is the new number is:
2 x 3 x 5 x 7 = 210
(ii) 3675 = 3 x 5 x 5 x 7 x 7

Grouping them into pairs of equal factors:
3675 = (5 x 5) x (7 x 7) x 3
The factor, 3 is not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 3675 must be multiplied by 3 for it to be a perfect square.
The new number would be (5 x 5) x (7 x 7) x (3 x 3).
Furthermore, we have:
(5 x 5) x (7 x 7) x (3 x 3) = (3 x 5 x 7) x (3 x 5 x 7)
Hence, the number whose square is the new number is:
3 x 5 x 7 = 105
(iii) 605 = 5 x 11 x 11

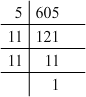
Grouping them into pairs of equal factors:
605 = 5 x (11 x 11)
The factor, 5 is not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 605 must be multiplied by 5 for it to be a perfect square.
The new number would be (5 x 5) x (11 x 11).
Furthermore, we have:
(5 x 5) x (11 x 11) = (5 x 11) x (5 x 11)
Hence, the number whose square is the new number is:
5 x 11 = 55
(iv) 2880 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 5

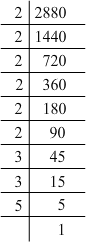
Grouping them into pairs of equal factors:
2880 = (2 x 2) x (2 x 2) x (2 x 2) x (3 x 3) x 5
There is a 5 as the leftover. For a number to be a perfect square, each prime factor has to be paired. Hence, 2880 must be multiplied by 5 to be a perfect square.
The new number would be (2 x 2) x (2 x 2) x (2 x 2) x (3 x 3) x (5 x 5).
Furthermore, we have:
(2 x 2) x (2 x 2) x (2 x 2) x (3 x 3) x (5 x 5) = (2 x 2 x 2 x 3 x 5) x (2 x 2 x 2 x 3 x 5)
Hence, the number whose square is the new number is:
2 x 2 x 2 x 3 x 5 = 120
(v) 4056 = 2 x 2 x 2 x 3 x 13 x 13

Grouping them into pairs of equal factors:
4056 = (2 x 2) x (13 x 13) x 2 x 3
The factors at the end, 2 and 3 are not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 4056 must be multiplied by 6 (2 x 3) for it to be a perfect square.
The new number would be (2 x 2) x (2 x 2) x (3 x 3) x (13 x 13).
Furthermore, we have:
(2 x 2) x (2 x 2) x (3 x 3) x (13 x 13) = (2 x 2 x 3 x 13) x (2 x 2 x 3 x 13)
Hence, the number whose square is the new number is:
2 x 2 x 3 x 13 = 156
(vi) 3468 = 2 x 2 x 3 x 17 x 17

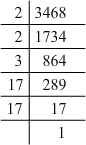
Grouping them into pairs of equal factors:
3468 = (2 x 2) x (17 x 17) x 3
The factor 3 is not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 3468 must be multiplied by 3 for it to be a perfect square.
The new number would be (2 x 2) x (17 x 17) x (3 x 3).
Furthermore, we have:
(2 x 2) x (17 x 17) x (3 x 3) = (2 x 3 x 17) x (2 x 3 x 17)
Hence, the number whose square is the new number is:
2 x 3 x 17 = 102
(vii) 7776 = 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 x 3 x 3

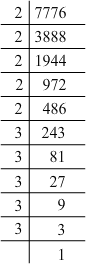
Grouping them into pairs of equal factors:
7776 = (2 x 2) x (2 x 2) x (3 x 3) x (3 x 3) x 2 x 3
The factors, 2 and 3 at the end are not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 7776 must be multiplied by 6 (2 x 3) for it to be a perfect square.
The new number would be (2 x 2) x (2 x 2) x (2 x 2) x (3 x 3) x (3 x 3) x (3 x 3).
Furthermore, we have:
(2 x 2) x (2 x 2) x (2 x 2) x (3 x 3) x (3 x 3) x (3 x 3) = (2 x 2 x 2 x 3 x 3 x 3) x (2 x 2 x 2 x 3 x 3 x 3)
Hence, the number whose square is the new number is:
2 x 2 x 2 x 3 x 3 x 3 = 216
Question 8: By what numbers should each of the following be divided to get a perfect square in each case? Also, find the number whose square is the new number.
(i) 16562
(ii) 3698
(iii) 5103
(iv) 3174
(v) 1575
Answer 8: Factorising each number.
(i) 16562 = 2 x 7 x 7 x 13 x 13

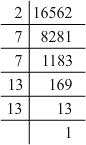
Grouping them into pairs of equal factors:
16562 = 2 x (7 x 7) x (13 x 13)
The factor, 2 is not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 16562 must be divided by 2 for it to be a perfect square.
The new number would be (7 x 7) x (13 x 13).
Furthermore, we have:
(7 x 7) x (13 x 13) = (7 x 13) x (7 x 13)
Hence, the number whose square is the new number is:
7 x 13 = 91
(ii) 3698 = 2 x 43 x 43

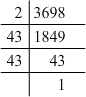
Grouping them into pairs of equal factors:
3698 = 2 x (43 x 43)
The factor, 2 is not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 3698 must be divided by 2 for it to be a perfect square.
The new number would be (43 x 43).
Hence, the number whose square is the new number is 43.
(iii) 5103 = 3 x 3 x 3 x 3 x 3 x 3 x 7

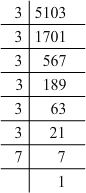
Grouping them into pairs of equal factors:
5103 = (3 x 3) x (3 x 3) x (3 x 3) x 7
The factor, 7 is not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 5103 must be divided by 7 for it to be a perfect square.
The new number would be (3 x 3) x (3 x 3) x (3 x 3).
Furthermore, we have:
(3 x 3) x (3 x 3) x (3 x 3) = (3 x 3 x 3) x (3 x 3 x 3)
Hence, the number whose square is the new number is:
3 x 3 x 3 = 27
(iv) 3174 = 2 x 3 x 23 x 23

Grouping them into pairs of equal factors:
3174 = 2 x 3 x (23 x 23)
The factors, 2 and 3 are not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 3174 must be divided by 6 (2 x 3) for it to be a perfect square.
The new number would be (23 x 23).
Hence, the number whose square is the new number is 23.
(v) 1575 = 3 x 3 x 5 x 5 x 7

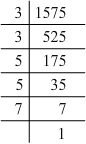
Grouping them into pairs of equal factors:
1575 = (3 x 3) x (5 x 5) x 7
The factor, 7 is not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 1575 must be divided by 7 for it to be a perfect square.
The new number would be (3 x 3) x (5 x 5).
Furthermore, we have:
(3 x 3) x (5 x 5) = (3 x 5) x (3 x 5)
Hence, the number whose square is the new number is:
3 x 5 = 15
QUESTION 9: FIND THE GREATEST NUMBER OF TWO DIGITS WHICH IS A PERFECT SQUARE.
ANSWER 9: WE KNOW THAT 102 IS EQUAL TO 100 AND 92 IS EQUAL TO 81.
SINCE 10 AND 9 ARE CONSECUTIVE NUMBERS, THERE IS NO PERFECT SQUARE BETWEEN 100 AND 81. SINCE 100 IS THE FIRST PERFECT SQUARE THAT HAS MORE THAN TWO DIGITS, 81 IS THE GREATEST TWO-DIGIT PERFECT SQUARE.

Question 10: Find the least number of three digits which is perfect square.
Answer 10: Let us make a list of the squares starting from 1.
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100
The square of 10 has three digits. Hence, the least three-digit perfect square is 100.
QUESTION 11: FIND THE SMALLEST NUMBER BY WHICH 4851 MUST BE MULTIPLIED SO THAT THE PRODUCT BECOMES A PERFECT SUQARE.
ANSWER 11: Prime factorisation of 4851:
4851 = 3 x 3 x 7 x 7 x 11
Grouping them into pairs of equal factors:
4851 = (3 x 3) x (7 x 7) x 11
The factor, 11 is not paired. The smallest number by which 4851 must be multiplied such that the resulting number is a perfect square is 11.
QUESTION 12: FIND THE SMALLEST NUMBER BY WHICH 28812 MUST BE DIVIDED SO THAT THE QUOTIENT BECOMES A PERFECT SQUARE.
ANSWER 12: Prime factorisation of 28812:
28812 = 2 x 2 x 3 x 7 x 7 x 7 x 7
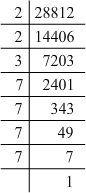Grouping them into pairs of equal factors:
28812 = (2 x 2) x (7 x 7) x (7 x 7) x 3
The factor, 3 is not paired. Hence, the smallest number by which 28812 must be divided such that the resulting number is a perfect square is 3.
QUESTION 13: FIND THE SMALLEST NUMBER BY WHICH 1152 MUST BE DIVIDED SO THAT IT BECOMES A PERFECT SQUARE. ALSO, FIND THE NUMBER WHOSE SQUARE IS THE RESULTING NUMBER.
ANSWER 13:
Prime factorisation of 1152:
1152 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3

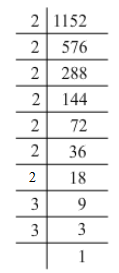
Grouping them into pairs of equal factors:
1152 = (2 x 2) x (2 x 2) x (2 x 2) x (3 x 3) x 2
The factor, 2 at the end is not paired. For a number to be a perfect square, each prime factor has to be paired. Hence, 1152 must be divided by 2 for it to be a perfect square.
The resulting number would be (2 x 2) x (2 x 2) x (2 x 2) x (3 x 3).
Furthermore, we have:
(2 x 2) x (2 x 2) x (2 x 2) x (2 x 2) x (3 x 3) = (2 x 2 x 2 x 3) x (2 x 2 x 2 x 3)
Hence, the number whose square is the resulting number is:
2 x 2 x 2 x 3 = 24.

The document Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics is a part of the Class 8 Course RD Sharma Solutions for Class 8 Mathematics.

All you need of Class 8 at this link: Class 8

	RD Sharma Solutions for Class 8 Mathematics 88 docs

RD Sharma Solutions for Class 8 Mathematics

88 docs

Join Course for Free

Top Courses for Class 8

View all

FAQs on Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics

1. What are squares and square roots?

Ans. Squares are the result of multiplying a number by itself. For example, the square of 3 is 3 multiplied by 3, which equals 9. Square roots, on the other hand, are the numbers that, when multiplied by themselves, give the original number. So, the square root of 9 is 3, because 3 multiplied by 3 equals 9.

2. How do I find the square root of a number?

Ans. To find the square root of a number, you can use the long division method or the prime factorization method. In the long division method, you divide the number into groups of two digits from right to left, starting with the largest perfect square less than or equal to the leftmost group. Then, you find the square root of the leftmost group and subtract the square of that number from the leftmost group. This process is repeated until all groups are covered. The number you get after subtracting the squares is the remainder. To find the square root, you bring down the next group of digits and repeat the process. In the prime factorization method, you express the number as a product of its prime factors, and then take the square root of each factor.

3. What is the value of the square root of 0?

Ans. The square root of 0 is 0. This is because 0 multiplied by 0 equals 0. In general, the square root of any number multiplied by itself will give the original number. Since 0 multiplied by 0 is 0, the square root of 0 is 0.

4. Can the square root of a negative number be determined?

Ans. No, the square root of a negative number cannot be determined using real numbers. This is because when we multiply a number by itself, the result is always positive or zero. For example, the square of 3 is 9, and the square of -3 is also 9. However, we can use complex numbers to determine the square root of a negative number. Complex numbers involve the use of imaginary numbers, where the square root of -1 is denoted as "i". So, the square root of -9 can be represented as 3i or -3i.

5. What are some real-life applications of squares and square roots?

Ans. Squares and square roots have various applications in real-life situations. Some examples include: 1. Architecture: Square roots are used in construction and architecture to determine the measurements of structures, ensuring proper dimensions and stability. 2. Electrical Engineering: Square roots are used in electrical engineering to calculate voltage, current, and resistance in circuits. 3. Finance and Investment: Square roots are used in financial calculations, such as calculating compound interest, risk analysis, and stock market forecasting. 4. Physics: Square roots are used in physics to calculate distances, velocities, and accelerations, as well as in formulas related to force, energy, and power. 5. Medical Imaging: Square roots are used in medical imaging techniques, such as MRI and CT scans, to reconstruct images from the data collected by the machines.

Related Exams

Class 8

About this Document

	4.61/5 Rating
	Nov 30, 2024 Last updated

Document Description: RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math for Class 8 2024 is part of RD Sharma Solutions for Class 8 Mathematics preparation. The notes and questions for RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math have been prepared according to the Class 8 exam syllabus. Information about RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math covers topics like and RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math Example, for Class 8 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math.

Introduction of RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math in English is available as part of our RD Sharma Solutions for Class 8 Mathematics for Class 8 & RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math in Hindi for RD Sharma Solutions for Class 8 Mathematics course. Download more important topics related with notes, lectures and mock test series for Class 8 Exam by signing up for free. Class 8: Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics

Description

Full syllabus notes, lecture & questions for Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics - Class 8 | Plus excerises question with solution to help you revise complete syllabus for RD Sharma Solutions for Class 8 Mathematics | Best notes, free PDF download

Information about RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math

In this doc you can find the meaning of RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math defined & explained in the simplest way possible. Besides explaining types of RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math theory, EduRev gives you an ample number of questions to practice RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math tests, examples and also practice Class 8 tests

	RD Sharma Solutions for Class 8 Mathematics 88 docs

RD Sharma Solutions for Class 8 Mathematics

88 docs

Join Course for Free

Download as PDF

Explore Courses for Class 8 exam

Top Courses for Class 8

Explore Courses

Signup for Free!

Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.

Start learning for Free

10M+ students study on EduRev

practice quizzes

Sample Paper

Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics

Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2

pdf

Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics

Objective type Questions

Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2

Free

Extra Questions

Important questions

Semester Notes

mock tests for examination

shortcuts and tricks

ppt

video lectures

Class 8 Math RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics

Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2

study material

Previous Year Questions with Solutions

Summary

MCQs

Viva Questions

Exam

past year papers

;

Additional Information about RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math for Class 8 Preparation

RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math Free PDF Download

The RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math is an invaluable resource that delves deep into the core of the Class 8 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math now and kickstart your journey towards success in the Class 8 exam.

Importance of RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math

The importance of RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math cannot be overstated, especially for Class 8 aspirants. This document holds the key to success in the Class 8 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math Notes

RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math Notes on EduRev are your ultimate resource for success.

RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math Class 8 Questions

The "RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math on the App

Students of Class 8 can study RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of RD Sharma Solutions - Chapter 3 - Squares and Square Roots (Ex-3.1) Part - 2, Class 8 Math is prepared as per the latest Class 8 syllabus.

Education Revolution

Signup to see your scores go up within 7 days!

Access 1000+ FREE Docs, Videos and Tests

Continue with Google

Takes less than 10 seconds to signup