Class 9 Math: Sample Question Paper- 8 (With Solutions) PDF Download
SECTION - A
Questions 1 to 20 carry 1 mark each.
Q.1. The total number of terms in the expansion of (x + a)501 + (x - a)501 is :
(a) 502
(b) 1004
(c) 251
(d) None of these
Ans: Choice (c) is correct.
We know that the total number of terms in the expansion of (x + a)n is (n + 1).
∴ Total number of terms in the expansion of (x + a)501 is (501 + 1) = 502.
Total number of terms in the expansion of (x + a)501 + (x - a)501 is 251 as 251 terms get cancelled.
Q.2. The value of the polynomial 5x - 4x2+ 3, when x = -1 is
(a) -6
(b) 6
(c) 2
(d) -2
OR
When p(x) = x4 - 3x2 + 2x + 1, is divided by (x-1), then the remainder obtained is :
(a) 1
(b) 2
(c) 0
(d) None of these
Ans: Correct option : (a)
Explanation:
When x = -1, the given polynomial
5x-42 +3 is
= 5(-l) - 4(-1)2 + 3
= - 5 + 4 + 3
= - 9 + 3 = -6
OR
Correct option : (a)
Explanation: By Remainder Theorem, the remainder
P(1)=(1)4-3(1)2+2(1)+1
= 1 -3 + 2 + 1 = 1
Q.3. If distance of a point P lie on the y-axis below x-axis is 5 unit the coordinates of P are :
(a) (0,5)
(b) (0,-5)
(c) (5,0)
(d) (-5,0)
Ans: (b) (0, -5)
Q.4. In a ΔABC, if 2∠A -3∠B = 6∠C, then the values of ∠A, ∠B and ∠C, is
(a) 90°, 60°, 30°
(b) 80°, 70°, 30°
(c) 70°, 40°, 70°
(d) None of these
Ans: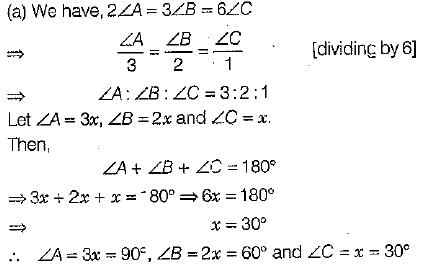
Q.5. Equation of y-axis is considered as
(a) x = 0, y = 0
(b) y = 0, z = 0
(c) z = 0, x = 0
(d) None of these
Ans: Choice (c) is correct.
On y-axis, x = 0, z = 0
Q.6. Which of the following is not true for a parallelogram?
(a) opposite sides are equal
(b) opposite angles are equal
(c) opposite angles are bisected by the diagonals
(d) diagonals bisect each other.
Ans: Correct option: (c)
Explanation: Opposite angles are bisected by the diagonals. This is not true for a parallelogram.
Q.7. In the given figure, ABCD is a parallelogram and L is the mid-point of DC. ifar(║gm ABCD) = 84 cm2, then ar(ΔACL) is :
(a) 21 cm2
(b) 42 cm2
(c) 36 cm2
(d) 24 cm2
Ans: (a) 21 cm2
[ ∵ AC is the diagonal of parallelogram ABCD
∴ 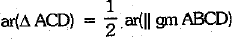 ...(i)
...(i)
Now, L is the mid-point of DC
∴ 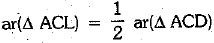 ...(ii)
...(ii)
From (i) and (ii), we have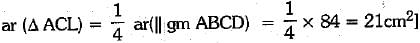
Q.8. If two complementary angles are such that one angle is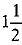 times the other, then the smaller angle among them is
times the other, then the smaller angle among them is
(a) 36°
(b) 42°
(c) 28°
(d) 34°
Ans: (a) Let one angle be x.
∴ Other angle =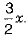
According to the question,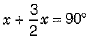
⇒ 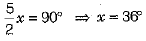
So the smaller angle is 36°.
Q.9. If a, b, c are in A.P., then
(a) b + c,b - c, be are also in A.P.
(b) ab,a + b,a - b, are also in A.P.
(c) b + c, c + a, a + b are also in A.P
(d) a + b, b - a, ab + ba are also in A.P
Ans: Choice (c) is correct.
b + c, c + a, a + b are in A.P
If b + c - (a + b + c)f c + a - (a - b + c), a + b - (a + b + c) are in A.P. [Subtracting (a + b + c)]
If - a, - b, - c are in A.P.
If a, b, c are in A.P., which is given to be true.
Q.10. A cone is 8.4 cm high and the radius of its base is 2.1 cm. It is melted and recast into a sphere. The radius of the sphere is
(a) 4.2 cm
(b) 2.1 cm
(c) 2.4 cm
(d) 1.6 cm
Ans: Correct option : (b)
Explanation.
Volume of sphere = Volume of cone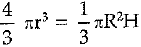
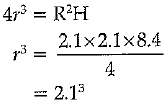
⇒ r = 2.1 cm.
(Q.11-15) Fill in the blanks :
Q.11. If p(x) = x3 - 3x2a + 2a2x + b is divisible by (x - a), then the value of b is________.
Or
If (x + 1) is a factor of a(x) = x98 4- 2x37 + d. then the value of p is_________.
Ans: zero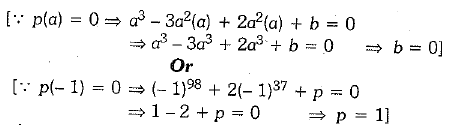
Q.12. Equal chords of congruent circles subtend equal angles at the_______.
Ans: Equal chords of congruent circles subtend equal angles at the centre.
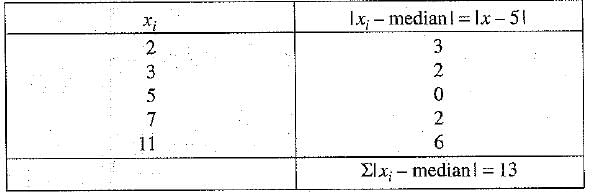
Q.13. The mean deviation from median of first five prime numbers is _______.
Ans: 2.6
The first five prime numbers are 2, 3, 5, 7, 11.
Numbers are in ascending order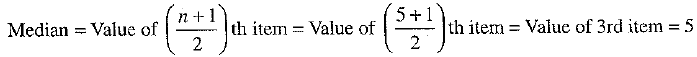
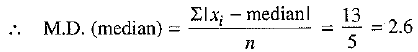
Q.14. PQRS and EFRS are two parallelograms, then ar (MFR)= ar
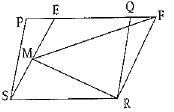
Ans: True
Explanation : v Area of two parallelograms between two parallel line and on same base and equal
∴ ar(parallelogram PQRS) = ar(parallelogram EFRS)
∵ Area of triangle is equal to half of parallelogram form on same base and lies between same two parallel lines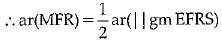
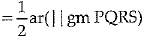
Q.15. If sum of 10.15.12.13,15.18.19.20 is 122, then mean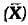 is________.
is________.
Ans: 15.25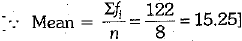
Directions (Q. Nos. 16-20) Answer the following questions.
Q.16. The cost of a note book is twice the cost of a pen. Write a linear equation in two variables to represent this statement.
Or
If (4, 19) is a solution of the equation y = ax + 3, then find the value of a.
Ans: Let the cost of a note book be Rs x and that of a pen to be Rs y. Then, according to the given statement we have
x =2y or 1.x - 2y + 0 = 0
Or
∵ (4,19) is a solution of y = ax + 3 ... (i)
On putting x = 4 and y = 19 in Eq. (i), we get
19 = a(4) + 3
⇒ 4a = 19-3 = 16
∴ a = 4
Q.17. If a parabola y2 = 4ax passes through point (3, 2), find the length of its latus rectum.
Ans: We know that the length of the latus rectum of parabola y2 = 4ax is 4a.
Parabola y2 = 4ax passes through the point (3, 2), the coordinates of the point satisfies the equation.
∴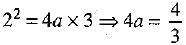
Hence, the length of latus rectum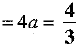
Q.18. Diagonals AC and BD of a parallelogram ABCD intersect each other at O. If OA = 3 cm and OD = 2 cm, determine the lengths of AC and BD.
Ans: AC = 6 cm , BD = 4 cm
Detailed Answer
We know that the diagonals of a parallelogram bisect each other.
Therefore,
AC = 2 x OA = 2 x 3 cm = 6 cm
BD = 2 x OD = 2 x 2 cm = 4 cm
Therefore, AC = 6 cm and BD = 4 cm.
Q.19. How many square metres of canvas is required for a conical tent whose height is 3.5 m and the radius of the base is 12 m ?
Ans: Here, radius of the base = 12 m
Height of the tent = 3.5 m
∴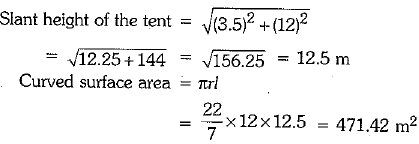
Hence, 471.42 sq. m of canvas is required to obtain the required conical tent.
Q.20. Find the total surface area of a cone whose radius is r/2 and slant height is 2l.
Ans: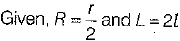
Total surface area of a cone = π(L + R)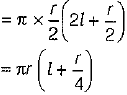
SECTION - B
Question numbers 21 to 26 carry 2 marks each.
21. Find n[(A ∪ B ∪ C)'] , if n(U) = 6500, n(A) = 4000, n(B) = 2000, n(C) = 1000 and n( A ∩ B) = n(B ∩ C = n(A ∩ C) = 400; n( A∩ B ∩ C) = 200.
OR
Let A = {1, 2,3}, B = {3,4} and C = {4,5,6}. Find
(i) A x (B ∩ C)
(ii) ( A x B ) ∩ ( A x C)
Ans: Given:
Given, n(U) = 6500, n(A) = 4000, n(B) = 2000, n(C) =1000, n(A ∩ B) = n(B ∩ C) = n(A ∩ C) = 400 and n(A ∩ B ∩ C) = 200
We know that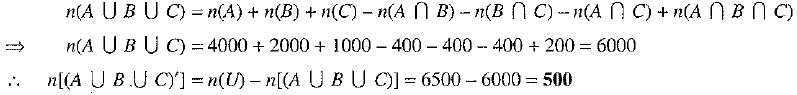
OR
We have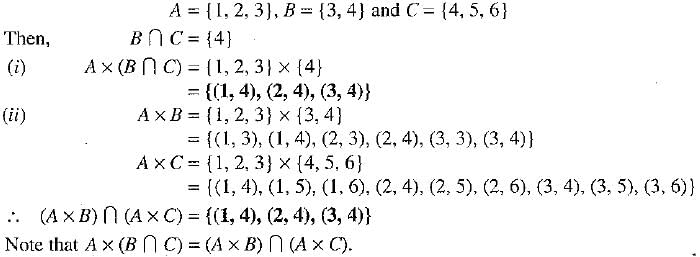
Q.22. Ram and Ravi have the same weight. If they each gain weight by 2kg, how will their new weights be compared?
Ans: Let x kg be the weight each of Ram and Ravi, On gaining 2 kg weight of Ram and Ravi's will be (x + 2) each. According to Euclid's second axiom, when equals are added to equals, the wholes are equal. So, weight of Ram and Ravi are again equal.
Q.23. Ram and Ravi have the same weight. If they each gain weight by 2 kg, how will their new weights be compared ?
Ans: Let x kg be the weight each of Ram and Ravi.
On adding 2 kg,
Weight of Ram and Ravi will be (x + 2) kg each.
According to Euclid's second axiom, when equals are added to equals, the wholes are equal.
So, weight of Ram and Ravi are again equal.
Q.24. ABC is an equilateral triangle and L, M and N are the mid-points of the sides AB, BC and CA, respectively. Prove that ΔLMN is an equilateral triangle.
Ans: Given ΔABC is an equilateral triangle and L, M and N are the mid-points of the sides AB,BC and CA, respectively.
To prove ΔLMN is an equilateral triangle.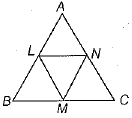

Q.25. From a class of 25 students, 10 are to be choosen for an excursion party. There are three students who decide that either all of them will join or none of them will join the party. Find in how many ways 10 students can be chosen ?
Ans: There are two possibilities namely :
(i) the particular 3 students join excursion party.
(ii) the particular 3 students do not join excursion party.
In the first case, we have to choose 7 students out of the remaining 22 students and this can be done in 22C7 ways.
In the second case, we have to choose 10 students out of the remaining 22 students and this can be done in 22C10 ways.
∴ The required number of ways = 22C7 + 22C10
Q.26. Find the mean of the data : 2, 8, 6, 5, 4, 5, 3, 6, 4, 9, 1, 5, 6, 5, 6.
Ans: 
SECTION - C
Question 27 to 34 carry 3 marks each.
Q.27. Find the domain and range of the real function f(x) =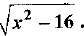
Ans: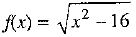
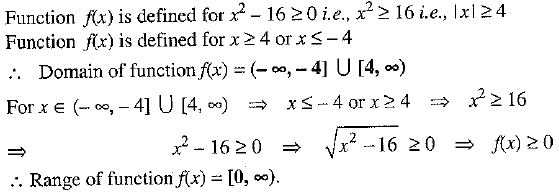
Q.28.Find the points on the line 2x + 3y = 12, where it cut the X and Y axes.
Ans: When x = 0 , y = 4 and when y = 0 , x = 6
The line meets the X axis at (6,0)
The line meets the Y axis at (0,4)
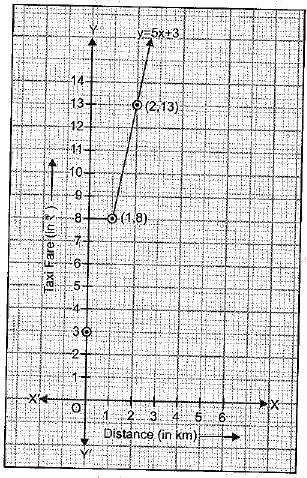
Q.29. The taxi fare in a city is as follows: For the first kilometre, the fare is Rs 8 and for the subsequent distance it is Rs 5 per km. Taking the distance covered as x km and total fare as Rs y, write a linear equation for this information, and draw its graph.
Ans: Given that,
Total distance covered= x km and total fare = Rs y, Since the fare for first kilometre is Rs 8 and fare for the remaining distance (x -1) km is Rs 5 per kilometre.
It can be written in the form of a linear equation in two variables as, 8 + 5(x- 1) = y.
Now, the equation becomes
y = 8 + 5x - 5
or y = 3 + 5x ...(i)
When x = 1
From equation (i) , we have
y = 3 + 5(1) =3 + 5 = 8
When x = 2
From equation (i), we have
y = 3 + 5(2) = 3 + 10 = 13
To draw the graph, we use the following table: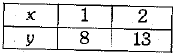
Q.30. If two isosceles triangles have a common base, then prove that the line segment joining their vertices bisects the common base at right angles.
Ans: Let ΔABC and ΔDBC are the given triangles with same base BC, in which AB = AC and DB = DC.
Also, let AD meets BC at E.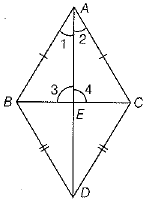

Q.31. The mean and standard deviation of 20 observations are found to be 10 and 2 respectively. On rechecking, it was found that an observation 8 was incorrect. Calculate the correct mean and standard deviation if the wrong item is replaced by 12.
OR
Two cards are drawn at random from a pack of 52 cards. Find the probability that the cards are either both red or both aces.
Ans: We have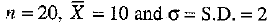
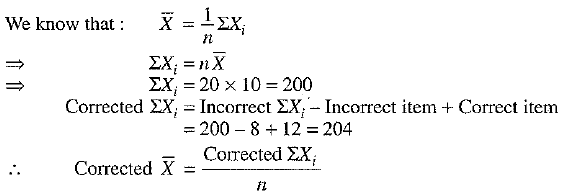 ...(1)
...(1)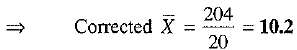 ...(2)
...(2)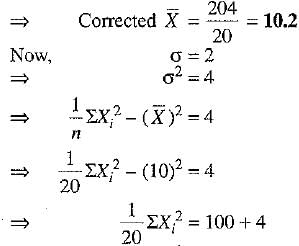
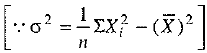
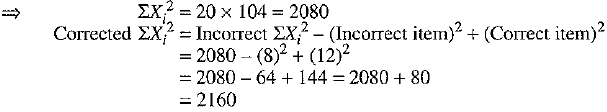 ...(3)
...(3) [using (2) and (4)]
[using (2) and (4)]
OR
Out of 52 cards, two cards can be drawn in 52C2 ways.
∴ Total number of elementary events =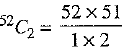
Let A = event that both cards drawn are red
and B = event that both cards drawn are aces
There are 26 red cards, out of which 2 red cards can be drawn in 26C2 =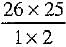
∴ 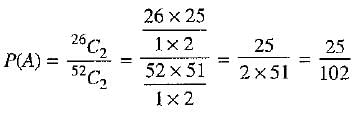
There are 4 aces, out of which 2 aces can be drawn in 4C2 =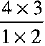
∴ 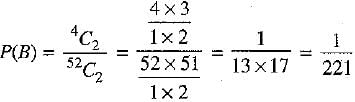
There are 2 cards which are both aces and red, out of which 2 cards can be drawn in 2C2 = 1
∴ 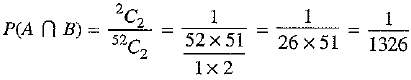
Required probability = Probability (both cards are red or both are aces) = P(A ∪ B)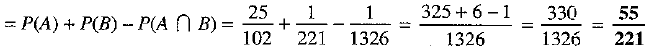
Q.32. In ΔABE, AE = BE. Circle through A and B intersects AE and BE at D and C. Prove that DC║AB
OR
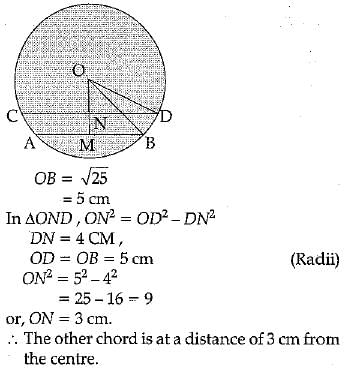
AB and CD are two parallel chords on the same side of the circle such that AB = 6 cm, CD = 8 cm. The small chord is at a distance of 4 cm from the centre. At what distance from the centre is the other chord ?
Ans:
Given
Q.33. Construct ΔXYZ in which ∠Y = 90% ∠Z — 30° and perimeter is 13 cm.
Ans: Given : In ΔXYZ, ZY = 90°, ∠Z = 30° and perimeter XY + YZ + ZX = 13 cm
Required: To construct ΔXYZ.
Steps of construction:
1. Draw any line seomentAB = 13 cm.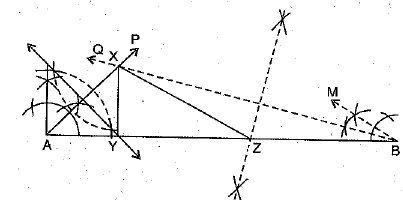
2. Construct ∠PAB == 45° and ∠QBA - 15° and say AP and BQ meet at X.
3. Draw the perpendicular bisector of AX and let it intersect AB at Y
4. Draw the perpendicular bisector of BX and let it intersect AB at Z.
5. Join XY and XZ.
Thus, ΔXYZ is the required triangle.
Q.34. A cylindrical road roller made of iron is 1 m wide. Its inner diameter is 54 cm and thickness of the iron sheet rolled into the road roller is 9 cm. Find the weight of the roller if 1 cm3 of iron weighs 8 gm.
Ans: The width of the road roller is 1 m i.e. 100 cm.
So, height (length) cf the cylinder = 100 cm
Inner radius of the cylinder = r = 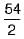 cm = 27 cm.
cm = 27 cm.
Thickness of the iron sheet = 9 cm.
Outer radius of the cylinder= R = (27 + 9)cm=36cm
Thus, volume of the iron sheet used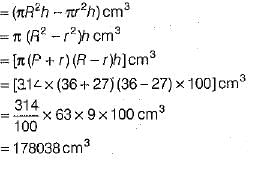
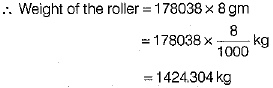
SECTION - D
Questions 35 to 40 carry 4 marks each
Q.35. Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science, 4 in English and Science, 4 in all the three. Find how many passed:
(i) in English and Mathematics but not in Science ?
(ii) in more than one subject only ?
Ans: Let E, M and S be the sets of students who passed English, Mathematics and Science respectively and U be set of all students.
According to given, we have
n(E) = 15, n(M) = 12, n(S) - 8, n(E ∩ M) = 6, n(M ∩ S) = 1, n(E ∩ S) = 4, n(E ∩ M ∩ S) = 4 and n(U) = 100.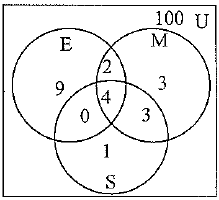
∴ Number of students who passed in English and Mathematics but not in Science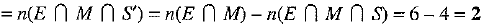
∴ Number of students who passed in two subjects only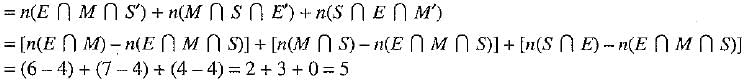
and the number of students who passed in all the three subjects = n(E ∩ M ∩ S) = 4
∴ Number of students who passed in more than two subjects
= Number of students who passed in two subjects only + Number of students who passed in all the three subjects
= 5 + 4 = 9
Q.36. If a + b + c = 6 and ab + be + ca = 11, find the value of a3 + b3 + c3 - 3abc.
OR
If x3 + mx2 - x + 6 has (x - 2) as a factor, and leaves a remainder V when divided by (x - 3), find the values of m and n.
Ans: 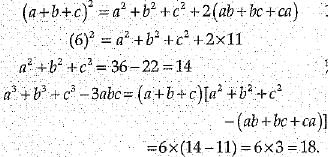
Or
Q.37. AB is a line segment and P is its mid-point, D and E are points on the same side of AB suck that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see fig). Show that:
(i) ΔDAP ≌ ΔEBP
(ii) AD = BE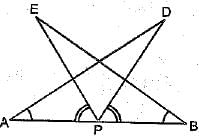
OR
AB and CD are respectively the smallest and longest sides of c quadrilateral ABCD (see fig.). Show that
∠A > ∠C and ∠B > ∠D.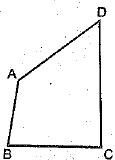
Ans: 'P' is the mid-point of AB
OR
Given: ABCD is a quadrilateral. AB is the shortest side and CD is the longest side
To Prove: ∠A > ∠C and ∠B > ∠D.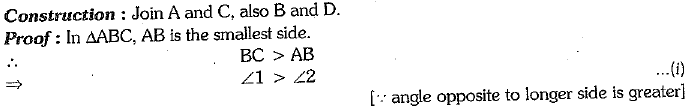

Q.38. If x1,x2,...., xn are n values of a variable x, such that 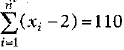 and
and
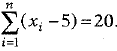 Find the value of n and the mean.
Find the value of n and the mean.
Or
Find the missing frequencies in the following frequency distribution, if it is known that the mean of the distribution is 1.46.
Ans:
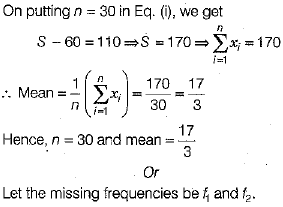

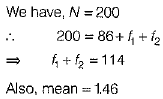 ...(i)
...(i)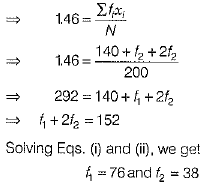 ...(ii)
...(ii)
Q.39. The sum of first three terms of a G.P. is 39/10 and their product is 1. Find the common ratio and the terms.
Or
Find the sum to n terms of the series 1 + 3 + 7 + 15 +...
Ans: Let the first three terms of a G.P.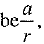 a and ar, respectively.
a and ar, respectively.
According to the given condition: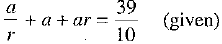 ...(i)
...(i)
and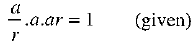 ...(ii)
...(ii)
From (2), we get
a3 = 1
⇒ a = 1 (consider only real roots)
Substituting a = 1 in (1), we have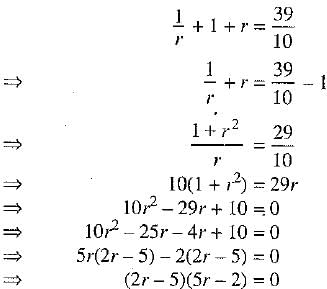 [∵ 10 x 10= 100 = 4 x 25]
[∵ 10 x 10= 100 = 4 x 25]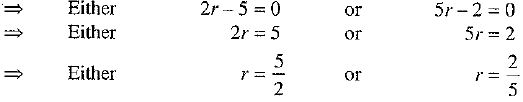
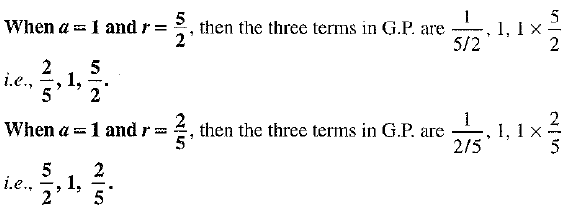
Or
The given series is
1 + 3 + 7 + 15 + ...
The sequence o f differences between successive terms is 2, 4, 8 ,...
Clearly, it is an G.P.
Let Tn denote nth term and Sn denote the sum of n terms of given series.
Sn = 1 + 3 + 7 + 15 + ... 4- Tn-1 + Tn ...(1)
Sn = 1 + 3 + 7 + 15 + ... +Tn-1 + Tn ...(2)
Subtracting (2) from (1), we get
0 = 1 + {2 + 4 + 8 + ... + (Tn - Tn-1)} - Tn
⇒ Tn = 1 + 2 + 4 + 8 + ... to n terms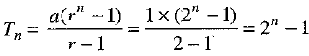
⇒ Tn = 2n - 1 ...(3)
Putting n = 1,2, 3,..., n, we get
T1 = 21 - 1 ...(4)
T2 = 22 - 1 ...(5)
T3 = 23 - l ...(6)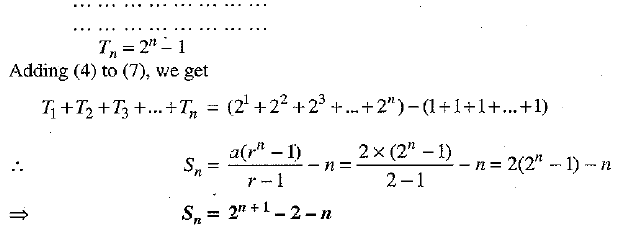 ...(7)
...(7)
Q.40. Construct a grouped frequency distribution table with class intervals 0 -5, 5 - 10 and so on for the following marks obtained in Biology (out of 50) by a group of 35 students in an examination:
0, 5, 6, 7, 10, 12, 14, 15, 20, 22, 25, 26, 27, 8, 11, 17, 3, 6, 9, 17, 19, 21, 22, 29, 31, 35, 37, 40, 42, 45, 49, 4, 50, 16.20 Also, draw a histogram to represent the above data.
Ans: A grouped frequency distribution table is a follows
The histogram for given data is shown below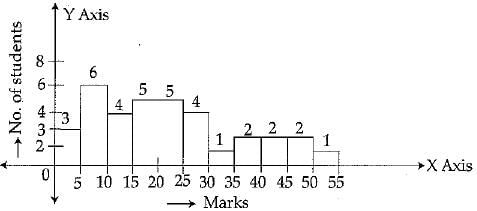
FAQs on Class 9 Math: Sample Question Paper- 8 (With Solutions)
| 1. What is the format of the Class 9 Math Sample Question Paper- 8? |  |
| 2. How many questions are included in the Class 9 Math Sample Question Paper- 8? |  |
| 3. Are the solutions provided for all the questions in the Class 9 Math Sample Question Paper- 8? |  |
| 4. How can the Class 9 Math Sample Question Paper- 8 be beneficial for exam preparation? |  |
| 5. Can the Class 9 Math Sample Question Paper- 8 be used as a study material? |  |














