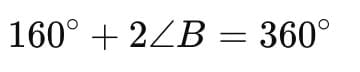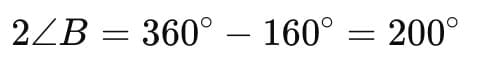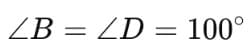Quadrilaterals Class 9 Worksheet Maths Chapter 8
Multiple Choice Questions
Q1: ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD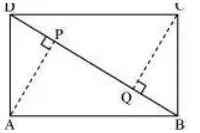 Which of the following is true based on given information
Which of the following is true based on given information
(a) AP = CQ
(b) QD = PB
(c) DP = QB
(d) ΔPAD ≅ ΔQCB
Ans: (a, b, c, d)
Sol: All are correct In Triangle ΔPAD and ΔQCB
AD = CB
∠P = ∠Q = 90º
∠CBQ = ∠ADP (Alternate interior angles of AB||CD)
So AAS congruence
Also as they are congruent, we get AP = CQ and DP = QB
Now Let's see the triangles ΔAPB and ΔCQD
AB = CD
∠P = ∠Q = 90º (Alternate interior angles of AB||CD)
So QD = PB
Q2: The angles of the quadrilateral are in the ratio 2 : 5 : 4 : 1? Which of the following is true?
(a) Largest angle in the quadrilateral is 150º
(b) Smallest angle is 30º
(c) The second largest angle in the quadrilateral is 80º
(d) None of these
Ans: (a, b)
Sol: Angles are 2 x , 5 x , 4 x , x
Now
2x + 5x + 4x + x = 360
Or x = 30
Angles are 30º, 60º, 120º, 150º
Q3: Two adjacent angles in a parallelogram are in the ratio 2 : 4. Find the values?
(a) 80, 100
(b) 40, 140
(c) 60, 120
(d) None of the above
Ans: (c)
Sol: Adjacent angles 2x + 4x = 180
x = 30
60, 120 are adjacent angles
Q4: ABCD is a trapezium with AB = 10cm, AD = 5 cm, BC = 4 cm and DC = 7 cm?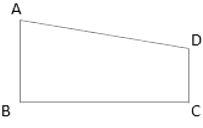 Find the area of the ABCD
Find the area of the ABCD
(a) 34 cm2
(b) 28cm2
(c) 20 cm2
(d) None of these
Ans: (a)
Sol: BC is the altitude between the two parallel sides AB and DC
So Area of trapezium will be given by
A = 1/2 BC (AB + DC) = 34cm2
Q5: ABCD is a trapezium where AB||DC. BD is the diagonal and E is the mid point of AD. A line is draw from point E parallel to AB intersecting BC at F. Which of these is true?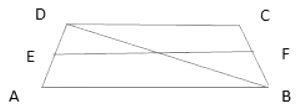 (a) BF = FC
(a) BF = FC
(b) EA = FB
(c) CF = DE
(d) None of these
Ans: (a)
Sol: Let’s call the point of intersection at diagonal as G
Then in triangle DAB
EG||AB and E is the mid point of DA, So by converse of Midpoint Theorem,
G is the mid point of BD
Now in triangle DBC
GF||CD
G is the mid point of DB
So by converse of mid point theorem
F is the mid point of BC
True or False
Q1: The diagonals of a parallelogram bisect each other.
Ans: True. It is by definition
Q2: In a parallelogram, opposite sides and angle are equal.
Ans: True. It is by definition
Q3: A diagonal of a parallelogram divides it into two congruent triangles.
Ans: True. This can be proved easily using SSS congruence
Q4: The bisectors of the angles of parallelogram create a rectangle.
Ans: True
Q5: Sum of all the internal angles is 360∘.
Ans: True. This can easily proved by drawing one diagonal and summing all the angles based on triangle angle sum.
Q6: Sum of all the exterior angles is 180∘.
Ans: False
Q7: Square, rectangle and rhombus are all parallelogram.
Ans: True
Q8: Consecutive angles are supplementary.
Ans: True
Answer the following Questions
Q1: Show that the quadrilateral formed by joining the mid- points of adjacent sides of rectangle is a rhombus.
Ans: The figure is shown as below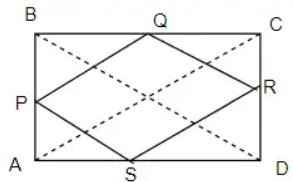
To Prove: quadrilateral PQRS is a rhombus
Proof:
In Δ ABC
P and Q are mid points of sides AB and BC
By Mid point theorem
PQ = 1/2 AC and PQ || AC -(X)
In Δ ACD
S and R are mid points of sides AD and DC
By Mid point theorem
SR = 1/2 AC and SR || AC --(Y)
From (X) and (Y), we have
PQ = SR
PQ ||SR
Hence PQRS is a parallelogram
Now in Δ BCD
Q and R are mid points of sides BC and DC
By Mid point theorem
QR = 1/2 BD
Nowe AC = BC
Hence
PQ = SR = QR
Now a parallelogram whose adjacent sides are equal is a rhombus.
Hence proved
Q2: P, Q, R and S are respectively the mid-point of sides AB, BC, CD and DA of a quadrilateral ABCD such that AC = BD. Prove that PQRS is a rhombus.
Ans:
Given AC = BD
Proof:
In Δ ABC
P and Q are mid points of sides AB and BC
By Mid point theorem
PQ = 1/2 AC and PQ || AC -(X)
In Δ ACD
S and R are mid points of sides AD and DC
By Mid point theorem
SR = 1/2 AC and SR || AC --(Y)
From (X) and (Y), we have
PQ = SR = 1/2 AC ----(1)
Similarly in Δ BCD
Q and R are mid point of BC and CD
By Mid point theorem
QR = 1/2 BD
Similarly in Δ ADB
S and P are mid point of AD and AB
By Mid point theorem
SP = 1/2 BD
Therefore
SP = QR = 1/2 BD ---(2)
AC = BD
So from (1) and (2)
PQ = SR = SP = QR
Hence PQRS is a rhombus
Q3: l, m and n are three parallel lines intersected by transversal's p and q such that l, m and n cut off equal intercepts AB and BC on p. Show that l, m and n cut off equal intercepts DE and EF on q also.
Ans:
Given:
AB = BC
To Prove:
DE = EF
Proof:
Let us join A to F intersecting m at G
The trapezium ACFD is divided into two triangles namely Δ ACF and & Δ AFD
In Δ ACF, it is given that B is the mid-point of AC (AB = BC) and BG || CF (since m || n).
So, G is the mid-point of AF (by Mid Point Theorem)
Now, in Δ AFD, we can apply the same argument as G is the mid-point of AF,
GE || AD and so by by Mid Point Theorem, E is the mid-point of DF,
i.e., DE = EF.
In other words, l, m and n cut off equal intercepts on q also.
Q4. Find all the angles of a parallelogram if one angle is 80°.
Ans: For a parallelogram ABCD, opposite angles are equal.
So, the angles opposite to the given 80° angle will also be 80°.
It is also known that the sum of angles of any quadrilateral = 360°.
So, if ∠A = ∠C = 80° then,
∠A + ∠B + ∠C + ∠D = 360°
Also, ∠B = ∠D
Thus,
80° + ∠B + 80° + ∠D = 360°
Hence, 2∠B = ∠D = 200°/2
Now, all angles of the quadrilateral are found which are:
∠A = 80°
∠B = 100°
∠C = 80°
∠D = 100°
Q5: In a trapezium ABCD, AB//CD. Calculate ∠C and ∠D if ∠A = 55° and ∠B = 70°
Ans: In a trapezium ABCD, ∠A + ∠D = 180° and ∠B + ∠C = 180°
So, 55° + ∠D = 180°
Or, ∠D = 125°
Similarly,
70° + ∠C = 180°
Or, ∠C = 110°
|
40 videos|471 docs|57 tests
|
FAQs on Quadrilaterals Class 9 Worksheet Maths Chapter 8
| 1. What are the different types of quadrilaterals? |  |
| 2. How do you calculate the area of a quadrilateral? |  |
| 3. What is the sum of the interior angles of a quadrilateral? |  |
| 4. What properties differentiate a parallelogram from a rectangle? |  |
| 5. How can you determine if a quadrilateral is a square? |  |