Class 9 Maths Number System CBSE Worksheets- 2
Q.1. What is the value of (23)2?
Solution:
(23)2 = 23x2 [∵ (xm)n = xm.n]
= 26 =2 x 2 x 2 x 2 x 2 x 2 = 64
Q.2. What is the value of (625) 1/4 ?
Solution:
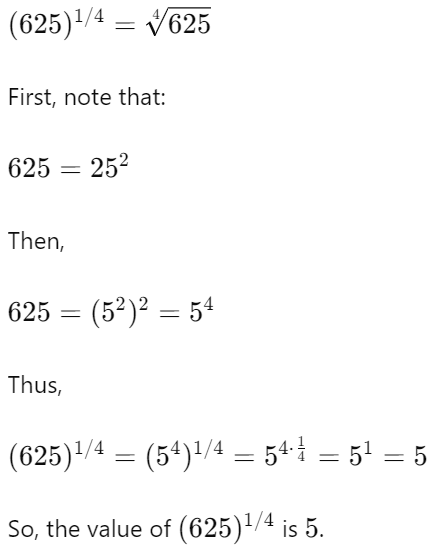
Q.3. Which of the following are irrational numbers?
√3, √4, √5, 22/7, π, 0
Solution: √3, √5 and π are irrational numbers.
√3: Irrational (cannot be expressed as a fraction of two integers)
√4: Rational (equals 2, which is an integer)
√5: Irrational (cannot be expressed as a fraction of two integers)
22/7: Rational (a fraction of two integers)
π: Irrational (cannot be expressed as a fraction of two integers)
0: Rational (can be expressed as 0/1)
Q.4. Which of the following are rational?
2√3, 1, 0, 3.14, π, 22/7
Solution: 1, 0, 3.14 and 22/7 are rational numbers.
2√3: Irrational (product of a rational and an irrational number)
1: Rational (an integer, can be expressed as 1/1)
0: Rational (can be expressed as 0/1)
3.14: Rational (a terminating decimal, can be expressed as 314/100)
π: Irrational (cannot be expressed as a fraction of two integers)
22/7: Rational (a fraction of two integers)
Q.5. Which of the following cube roots is not irrational?
3 √5, 3√6, 3√7, 3√8, 3√9
Solution: 3√8 is not an irrational number.
Q.6. Which three integers are equal to their own cube roots?
Solution: –1, 0 and 1
[∵ 3√-1 = -1, 3√1 = 1 and 3√0 = 0 ]
Q.7. Is the following number rational or irrational? 0.0769230769230769230...
Solution:
The given number is rational.
The number 0.076923076923076923... is a repeating decimal. The number is rational because it has a repeating pattern and can be expressed as a fraction of two integers.
Q.8. Is 0.666 ...a “non-terminating rational” or “non-terminating recurring rational number”?
Solution: Non-terminating recurring rational number.
0.666... (where the 6 repeats indefinitely) is a repeating decimal. It is a non-terminating recurring rational number because it has a repeating pattern and can be expressed as a fraction (specifically, 2/3).
Q.9. Is 1.27 27 27 ... non-terminating recurring or non-terminating non-recurring number?
Solution: It is a non-terminating recurring rational number.
1.272727... (where 27 repeats indefinitely) is a repeating decimal. It is a non-terminating recurring rational number because it has a repeating pattern and can be expressed as a fraction.
Q.10. The decimal representation of √3 is 1.73205807... . Is it non-terminating nonrecurring?
Solution: Yes
The decimal representation of √3 does not repeat and does not terminate.
Q.11. Is the product of a rational and an irrational number, rational?
Solution: No. It is an irrational number.
Q.12. Write the smallest non-negative integer.
Solution: The smallest non-negative integer is ‘0’.
Q.13. Write the smallest positive integer.
Solution: The smallest positive integer is '1'.
Q.14. Up to how many decimal places, π and 22/7 are same?
Solution: π and 22/7 are same only up to 2 decimal places.
[∵ 22/7 = 3.142857142... and π =3.141592653589...]
Q.15. Which of the following is irrational?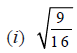
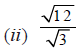
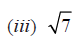
Solution: √7 is irrational.
Q.16. Which of the following is the value of 0.999... expressed as p/q :
(i) 9/10
(ii) 1
(iii) 999/1000
Solution:(ii) = 1
|
40 videos|471 docs|57 tests
|
FAQs on Class 9 Maths Number System CBSE Worksheets- 2
| 1. What is the number system? |  |
| 2. What are natural numbers? |  |
| 3. What is the difference between whole numbers and natural numbers? |  |
| 4. How are rational numbers represented? |  |
| 5. What are irrational numbers? |  |























