Indices and Bases
- In this document, we are going to be looking at logarithms. However, before we can deal with logarithms. we need to revise indices.
- This is because logarithms and indices are closely related, and to understand logarithms a good knowledge of indices is required.
- We know that, 16 = 24
- Here, the number 4 is the power. Sometimes we call it an exponent. Sometimes we call it an index. In the expression 24, the number 2 is called the base.
 Logarithms
Logarithms
Why do we study logarithms?
- To understand logarithms, consider the following: we know that 16 = 24. We also know that 8 = 23
- Suppose that we wanted to multiply 16 by 8.
- One way is to carry out the multiplication directly using long multiplication and obtain 128.
- But this could be long and tedious if the numbers were larger than 8 and 16. Can we do this calculation another way using the powers?
- Note that 6 × 8 can be written 24 × 23
This equals 27
Using the rules of indices which tell us to add the powers 4 and 3 to give a new power, 7. - What was a multiplication sum has been reduced to an addition sum. Similarly, if we wanted to divide 16 by 8: 16 ÷ 8 can be written 24 ÷ 23
- This equals 21 or simply 2
- Using the rules of indices which tell us to subtract the powers 4 and 3 to give the new power, 1.
- If we had a look-up table containing powers of 2, it would be straightforward to look up 27 and obtain 27 = 128 as the result of finding 16 × 8.
- Notice that by using the powers, we have changed a multiplication problem into one involving addition (the addition of the powers, 4 and 3).
- Historically, this observation led John Napier (1550-1617) and Henry Briggs (1561-1630) to develop logarithms as a way of replacing multiplication with addition, and also division with subtraction.
What is a Logarithm?
- Consider the expression 16 = 24. Remember that 2 is the base, and 4 is the power.
- An alternative, yet equivalent, way of writing this expression is log2 16 = 4. This is stated as ‘log to base 2 of 16 equals 4’.
- We see that the logarithm is the same as the power or index in the original expression.
- It is the base in the original expression which becomes the base of the logarithm.
- The two statements:16 = 24, and log2 16 = 4 are equivalent statements.
- If we write either of them, we are automatically implying the other.
- Example: If we write down 64 = 82, then the equivalent statement using logarithms is log8 64 = 2.
- Example: If we write down log3 27 = 3, then the equivalent statement using powers is 33 = 27.
So the two sets of statements, one involving powers and one involving logarithms are equivalent.
In the general case, we have:
Key Point
if x = an then equivalently loga x = n
loga a = 1
- Let us develop this a little more.
As 10 = 101 we can write the equivalent logarithmic form log10 10 = 1. - Similarly, the logarithmic form of the statement 21 = 2 is log2 2 = 1.
- In general, for any base a, a = a1 and so loga a = 1.
We can see from the Examples above that indices and logarithms are very closely related. In the same way that we have rules or laws of indices, we have laws of logarithms. These are developed in the following sections.
Types of Logarithms
There are two main types of logarithms that we commonly use: common logarithms and natural logarithms.
1. Common Logarithm:
- Also known as base 10 logarithms, it's denoted as log10 or simply log.
- For instance, log (1000) is a common logarithm, representing how many times we need to multiply 10 to get the desired result.
- For example, log (100) equals 2 because multiplying 10 by itself twice gives 100.
2. Natural Logarithm:
- Also called base e logarithms, it's represented as ln or loge.
- Here, "e" stands for Euler’s constant, which is around 2.71828.
- For instance, ln (78) is a natural logarithm, indicating how many times we need to multiply "e" to get the desired result.
- For example, ln (78) equals 4.357, meaning we have to multiply "e" by itself around 4.357 times to get 78.
Rules for Logarithmic Operations
1. Product Rule
When you multiply two logarithmic values, it's like adding their individual logarithms:
logb(mn) = logbm + logbn
2. Division Rule
Dividing two logarithmic values is like subtracting their individual logarithms:
logb(m/n) = logbm - logbn
3. Exponential Rule
The logarithm of a product with a rational exponent is equal to the exponent times its logarithm:
logb(mn) = n logbm
4. Change of Base Rule
Switching between different bases is done by dividing the logarithm in the original base by the logarithm in the new base:
logbm = logam / logab
5. Base Switch Rule
Inverting the logarithm's base is done by taking the reciprocal of the logarithm in the new base:
logba = 1 / logab
6. Derivative of Log
If f(x) = logb(x), then the derivative of f(x) is given by:
f'(x) = 1 / (x ln(b))
7. Integral of Log
The integral of a logarithmic function is given by:
∫logb(x)dx = x(logb(x) - 1/ln(b)) + C
Other Properties
- logbb = 1
- logb1 = 0
- logb0 = undefined
Using Logarithms to Solve Equations
We can use logarithms to solve equations where the unknown is in the power. Suppose we wish to solve the equation 3x = 5. We can solve this by taking logarithms of both sides. Whilst logarithms to any base can be used, it is common practice to use base 10, as these are readily available on your calculator. So, log 3x = log 5
Now using the laws of logarithms, the left-hand side can be re-written to give
x log 3 = log 5
This is more straightforward. The unknown is no longer in the power. Straightaway If we want, this value can be found in a calculator.
If we want, this value can be found in a calculator.
Solved Examples on Logarithms
Example 1: Suppose we wish to find log2 512.
This is the same as being asked ‘What is 512 expressed as a power of 2 ?’
Now 512 is 29 and so log2 512 = 9.
Example 2: Suppose we wish to find log8 1/64.
This is the same as being asked ‘What is 1/64 expressed as a power of 8 ?’
Now 1/64 can be written 64−1. Noting also that 82 = 64 it follows that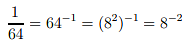
using the rules of indices. So log8 = 1/64 = -2
Example 3: Suppose we wish to find log5 25.
This is the same as being asked ‘What is 25 expressed as a power of 5 ?’
Now 52 = 25 and so log5 25 = 2.
Example 4: Suppose we wish to find log25 5.
This is the same as being asked ‘What is 5 expressed as a power of 25 ?’
We know that 5 is a square root of 25, that is 5 = √25. So 25 1/2 = 5 and so log25 5 = 1/2.
Example 5: Consider log2 8. We are asking ‘What is 8 expressed as a power of 2 ?’ We know that 8 = 23 and so log2 8 = 3.
What about log8 2 ? Now we are asking ‘What is 2 expressed as a power of 8 ?’ Now 23 = 8 and so 2 = ∛8 or 81/3. So log8 2 =1/3.
We see again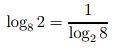
FAQs on Logarithm: Concepts with Examples - JEE
| 1. Why do we study logarithms? |  |
| 2. What is a Logarithm? |  |
| 3. What are the types of logarithms? |  |
| 4. What are the rules for logarithmic operations? |  |
| 5. How can logarithms be used to solve equations? |  |



















