Chapter 21 - Mensuration - II (Part - 4), Class 8, Maths RD Sharma Solutions | RD Sharma Solutions for Class 8 Mathematics PDF Download
PAGE NO 21.30:
Question 1:
Find the length of the longest rod that can be placed in a room 12 m long, 9 m broad and 8 m high.
ANSWER:
Length of the room = 12 m
Breadth = 9 m
Height = 8 m
Since the room is cuboidal in shape, the length of the longest rod that can be placed in the room will be equal to the length of the diagonal between opposite vertices.
Length of the diagonal of the floor using the Pythagorus theorem
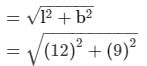
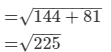
= 15 m
i.e., the length of the longest rod would be equal to the length of the diagonal of the right angle triangle of base 15 m and altitude 8 m.
Similarly, using the Pythagorus theorem, length of the diagonal
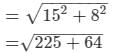 = 17 m
= 17 m
∴ The length of the longest rod that can be placed in the room is 17 m.
Question 2:
If V is the volume of a cuboid of dimensions a, b, c and S is its surface area, then prove that 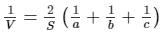
ANSWER:
It is given that V is the volume of a cuboid of length = a, breadth = b and height = c.
Also, S is surface area of cuboid.Then, V = a × b × c
Surface area of the cuboid = 2 × (length × breadth + breadth × height + length × height)
⇒ S = 2 × (a × b + b × c + a × c)
Let us take the right−hand side of the equation to be proven.
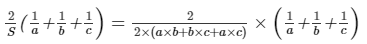
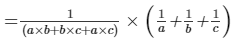
Now, multiplying the numerator and the denominator with a × b × c,
we get:1(a × b + b × c + a × c) × (1a + 1b + 1c) × a × b × ca × b × c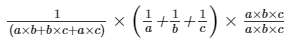

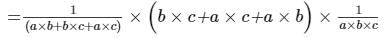
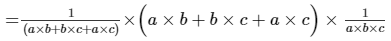
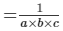
= 1/V
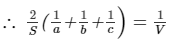
Question 3:
The areas of three adjacent faces of a cuboid are x, y and z. If the volume is V, prove that V2 = xyz.
ANSWER:
The areas of three adjacent faces of a cuboid are x, y and z.
Volume of the cuboid = V
Observe that x = length × breadth y = breadth × height, z = length × height
Since volume of cuboid V = length × breadth × height,
we have:V2 = V × V
= (length × breadth × height) × (length × breadth × height)
= (length × breadth) × (breadth × height) × (length × height) = x × y × z = xyz
∴ V2 = xyz
Question 4:
A rectangular water reservoir contains 105 m³ of water. Find the depth of the water in the reservoir if its base measures 12 m by 3.5 m.
ANSWER:
Length of the rectangular water reservoir = 12 m
Breadth = 3.5 m
Suppose that the height of the reservoir = h m
Also, it contains 105 m³ of water, i.e., its volume = 105 m³
Volume of the cuboidal water reservoir = length × breadth × height
⇒ 105 = 12 × 3.5 × h
⇒ 105 = 42 × h
⇒ h = 105/42 = 2.5 m
∴ The depth of the water in the reservoir is 2.5 m.
Question 5:
Cubes A, B, C having edges 18 cm, 24 cm and 30 cm respectively are melted and moulded into a new cube D. Find the edge of the bigger cube D.
ANSWER:
We have the following:Length of the edge of cube A = 18 cm
Length of the edge of cube B = 24 cm
Length of the edge of cube C = 30 cm
The given cubes are melted and moulded into a new cube D.
Hence, volume of cube D = volume of cube A + volume of cube B + volume of cube C
= (side of cube A)3 + (side of cube B)3 + (side of cube C)3
= 183 + 243 + 303
= 5832 + 13824 + 27000 = 46656 cm³
Suppose that the edge of the new cube D = x
⇒ x3 = 46656
⇒ 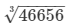 = 36 cm
= 36 cm
∴ The edge of the bigger cube D is 36 cm.
Question 6:
The breadth of a room is twice its height, one half of its length and the volume of the room is 512 cu. dm. Find its dimensions.
ANSWER:
Suppose that the breadth of the room = x dm
Since breadth is twice the height, breadth = 2 × height
So, height of the room = breadth/2 = x/2
Also, it is given that the breadth is half the length.
So, breadth = 1/2 × length
i.e., length = 2 × breadth = 2 × x
Since volume of the room = 512 cu dm,
we have:Volume of a cuboid = length × breadth × height
⇒ 512 = 2 × x × x × x/2
⇒ 512 = x3
⇒ x = 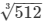 = 8 dm
= 8 dm
Hence, length of the room = 2 × x = 2 × 8 = 16 dm
Breadth of the room = x = 8 dm
Height of the the room = x/2 = 8/2 = 4 dm
Question 7:
A closed iron tank 12 m long, 9 m wide and 4 m deep is to be made. Determine the cost of iron sheet used at the rate of Rs 5 per metre sheet, sheet being 2 m wide.
ANSWER:
A closed iron tank of dimensions 12 m long, 9 m wide and 4 m deep is to be made.
Surface area of the cuboidal tank = 2 × (length × breadth + breadth × height + length × height)
= 2 × (12 × 9 + 9 × 4 + 12 × 4)
= 2 × (108 + 36 + 48) = 384 m²
Also, the cost of an iron sheet is Rs 5 per metre and the sheet is 2 metres wide.
i.e., area of a sheet = 1 m × 2 m = 2 m²
So, the cost of 2 m² of iron sheet = Rs 5
i.e., the cost of 1 m² of iron sheet = Rs 5/2
∴ Cost of 384 m² of iron sheet = 384 × 5/2 = Rs 960
Question 8:
A tank open at the top is made of iron sheet 4 m wide. If the dimensions of the tank are 12 m × 8 m × 6 m, find the cost of iron sheet at Rs 17.50 per metre.
ANSWER:
An open iron tank of dimensions 12 m × 8 m × 6 m is to be made.
Surface area of the open tank = (area of the base) + (total area of the 4 walls) = (12 × 8) + 2 × (8 × 6 + 12 × 6) = (96) + 2 × (48 + 72) = 336 m²
Also, it is given that the cost of the iron sheet that is 4 m wide is Rs 17.50 per metre.
i.e., the area of the iron sheet = 1 m × 4 m = 4 m²
So, the cost of 4 m² of iron sheet = Rs 17.50
∴ The cost of iron sheet required to an iron tank of surface area 336 m² = 336 × 17.50/4 = Rs 1470
Question 9:
Three equal cubes are placed adjacently in a row. Find the ratio of total surface area of the new cuboid to that of the sum of the surface areas of the three cubes.
ANSWER:
Suppose that the side of the cube = x cm
Surface area of the cube = 6 × (side)2 = 6 × x2 = 6x2 cm²
i.e., the sum of the surface areas of three such cubes = 6x2 + 6x2 + 6x2 = 18 x2 cm²
Now, these three cubes area placed together to form a cuboid.
Then the length of the new cuboid will be 3 times the edge of the cube = 3 × x = 3x cm
Breadth of the cuboid = x cm
Height of the cuboid = x cm
∴ Total surface area of the cuboid = 2 × (length × breadth + breadth × height + length × height)
= 2 × (3x × x + x × x + 3x × x)
= 2 × (3x2 + x2 + 3x2) = 2 × (7x2)
= 14x2 cm
i.e., the ratio of the total surface area cuboid to the sum of the surface areas of the three cubes = 14 x2 cm² : 18 x2 cm²
= 7:9 14 x2 cm² : 18 x2 cm²
= 7:9
Hence, the ratio is 7:9.
Question 10:
The dimensions of a room are 12.5 m by 9 m by 7 m. There are 2 doors and 4 windows in the room; each door measures 2.5 m by 1.2 m and each window 1.5 m by 1 m. Find the cost of painting the walls at Rs 3.50 per square metre.
ANSWER:
The dimensions of the room are 12.5 m × 9 m × 7 m.
Hence, the surface area of walls = 2 × (length × height + breadth × height) = 2 × (12.5 × 7 + 9 × 7) = 301 m²
Also, there are 2 doors and 4 windows in the room. The dimensions of door are 2.5 m × 1.2 m.
i.e., area of a door = 2.5 × 1.2 = 3 m²
∴ Total area of 2 doors = 2 × 3 = 6 m²
The dimensions of a window are 1.5 m × 1 m. i.e., area of a window = 1.5 × 1 = 1.5 m²
∴ Total area of 4 windows = 4 × 1.5 = 6 m²
Hence, the total area to be painted = 301−(6 + 6) = 289 m²
The rate of painting 1 m² of wall = Rs 3.50
∴ The total cost of painting 289 m² of wall = Rs 289 × 3.50 = Rs 1011.50
Question 11:
A field is 150 m long and 100 m wide. A plot (outside the field) 50 m long and 30 m wide is dug to a depth of 8 m and the earth taken out from the plot is spread evenly in the field. By how much is the level of field raised?
ANSWER:
The dimensions of the plot dug outside the field are 50 m × 30 m × 8 m.
Hence, volume of the earth dug−out from the plot = 50 × 30 × 8 = 12000 m³
Suppose that the level of the earth rises by h m.
When we spread this dug−out earth on the field of length 150 m, breadth 100 m and height h m,
we have:
Volume of earth dug−out = 150 × 100 × h
⇒ 12000 = 15000 × h
⇒ h = 12000/15000 = 0.8 m
⇒ h = 80 cm (∵ 1 m = 100 cm)
∴ The level of the field will rise by 80 cm.
Question 12:
Two cubes, each of volume 512 cm³ are joined end to end. Find the surface area of the resulting cuboid.
ANSWER:
Two cubes each of volume 512 cm³ are joined end to end. Now, volume of a cube = (side)3
⇒ 512 = (side)3
⇒ Side of the cube =  = 8 cm
= 8 cm
If the cubes area joined side by side, then the length of the resulting cuboid is 2 × 8 cm = 16 cm.
Breadth = 8 cm
Height = 8 cm
∴ Surface area of the cuboid = 2 × (length × breadth + breadth × height + length × height)
= 2 × (16 × 8 + 8 × 8 + 16 × 8)
= 2 × (128 + 64 + 128)
= 640 cm²
Question 13:
Three cubes whose edges measure 3 cm, 4 cm, and 5 cm respectively are melted to form a new cube. Find the surface area of the new cube formed.
ANSWER:
Three cubes of edges 3 cm, 4 cm and 5 cm are melted and molded to form a new cube.
i.e., volume of the new cube = sum of the volumes of the three cubes = (3)3 + (4)3 + (5)3
= 27 + 64 + 125 = 216 cm³
We know that volume of a cube = (side)3
⇒ 216 = (side)3
⇒ Side of the new cube = 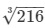 = 6 cm
= 6 cm
∴ Surface area of the new cube = 6 × (side)2 = 6 × (6)2 = 216 cm²
Question 14:
The cost of preparing the walls of a room 12 m long at the rate of Rs 1.35 per square metre is Rs 340.20 and the cost of matting the floor at 85 paise per square metre is Rs 91.80. Find the height of the room.
ANSWER:
The cost of preparing 4 walls of a room whose length is 12 m is Rs 340.20 at a rate of Rs 1.35/m².
∴ Area of the four walls of the room = 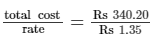 = 252 m²
= 252 m²
Also, the cost of matting the floor at 85 paise/m² is Rs 91.80.
∴ Area of the floor = 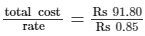 = 108 m²
= 108 m²
Hence, breadth of the room = 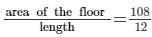 = 9 m
= 9 m
Suppose that the height of the room is h m.
Then, we have:Area of four walls = 2 × (length × height + breadth × height)
⇒ 252 = 2 × (12 × h + 9 × h)
⇒ 252 = 2 × (21h)
⇒ 21h = 252/2 = 126
⇒ h = 126/21 = 6 m
∴ The height of the room is 6 m.
Question 15:
The length of a hall is 18 m and the width 12 m. The sum of the areas of the floor and the flat roof is equal to the sum of the areas of the four walls. Find the height of the wall.
ANSWER:
Length of the hall = 18 m
Its width = 12 m Suppose that the height of the wall is h m.
Also, sum of the areas of the floor and the flat roof = sum of the areas of the four walls
⇒ 2 × (length × breadth) = 2 × (length + breadth) × height
⇒ 2 × (18 × 12) = 2 × (18 + 12) × h
⇒ 432 = 60 × h
⇒ h = 432/60 = 7.2 m
∴ The height of wall is 7.2 m
Question 16:
A metal cube of edge 12 cm is melted and formed into three smaller cubes. If the edges of the two smaller cubes are 6 cm and 8 cm, find the edge of the third smaller cube.
ANSWER:
Let the edge of the third cube be x cm.
Three small cubes are formed by melting the cube of edge 12 cm.
Edges of two small cubes are 6 cm and 8 cm.
Now, volume of a cube = (side)3
Volume of the big cube = sum of the volumes of the three small cubes
⇒ (12)3 = (6)3 + (8)3 + (x)3
⇒ 1728 = 216 + 512 + x3
⇒ x3 = 1728−728 = 1000
⇒ x = 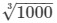 = 10 cm
= 10 cm
∴ The edge of the third cube is 10 cm.
Question 17:
The dimensions of a cinema hall are 100 m, 50 m and 18 m. How many persons can sit in the hall, if each person requires 150 m³ of air?
ANSWER:
The dimensions of a cinema hall are 100 m × 50 m × 18 m.
i.e., volume of air in the cinema hall = 100 × 50 × 18 = 90000 m³
It is given that each person requires 150 m³ of air.
∴ The number of persons that can sit in the cinema hall = 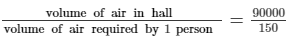 = 600
= 600
Question 18:
The external dimensions of a closed wooden box are 48 cm, 36 cm, 30 cm. The box is made of 1.5 cm thick wood. How many bricks of size 6 cm × 3 cm × 0.75 cm can be put in this box?
ANSWER:
The outer dimensions of the closed wooden box are 48 cm × 36 cm × 30 cm.
Also, the box is made of a 1.5 cm thick wood, so the inner dimensions of the box will be (2 × 1.5 = 3)cm less.
i.e., the inner dimensions of the box are 45 cm × 33 cm × 27 cm
∴ Volume of the box = 45 × 33 × 27 = 40095 cm³
Also, the dimensions of a brick are 6 cm × 3 cm × 0.75 cm.
Volume of a brick = 6 × 3 × 0.75 = 13.5 cm³
∴ The number of bricks that can be put in the box = 40095/13.5 = 2970
PAGE NO 21.31:
Question 19:
The dimensions of a rectangular box are in the ratio of 2 : 3 : 4 and the difference between the cost of covering it with sheet of paper at the rates of Rs 8 and Rs 9.50 per m² is Rs. 1248. Find the dimensions of the box.
ANSWER:
Suppose that the dimensions be x multiple of each other.
The dimensions are in the ratio 2:3:4.
Hence, length = 2x m
Breadth = 3x m
Height = 4x m
So, total surface area of the rectangular box = 2 × (length × breadth + breadth × height + length × height)
= 2 × (2x × 3x + 3x × 4x + 2x × 4x)
= 2 × (6x2 + 12x2 + 8x2)
= 2 × (26x2)
= 52x2 m²
Also, the cost of covering the box with paper at the rate Rs 8/m² and Rs 9.50/m² is Rs 1248.
Here, the total cost of covering the box at a rate of Rs 8/m² = 8 × 52x2 = Rs 416x2
And the total cost of covering the box at a rate of Rs 9.50/m² = 9.50 × 52x2 = Rs 494x2
Now, total cost of covering the box at the rate Rs 9.50/m²−total cost of covering the box at the rate Rs 8/m² = 1248
⇒ 494x2−416x2 = 1248
⇒ 78x2 = 1248
⇒ x2 = 1248/78 = 16
⇒ x = 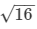 = 4
= 4
Hence, length of the rectangular box = 2 × x = 2 × 4 = 8 m
Breadth = 3 × x = 3 × 4 = 12 m
Height = 4 × x = 4 × 4 = 16 m
FAQs on Chapter 21 - Mensuration - II (Part - 4), Class 8, Maths RD Sharma Solutions - RD Sharma Solutions for Class 8 Mathematics
| 1. What are the different formulas used in mensuration? |  |
| 2. How do I find the surface area of a rectangular prism? |  |
| 3. How do I calculate the volume of a cone? |  |
| 4. What is the formula for the volume of a pyramid? |  |
| 5. How do I find the surface area of a sphere? |  |
















