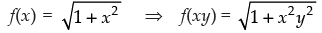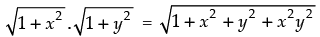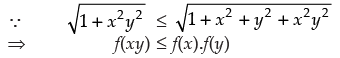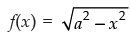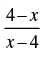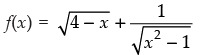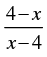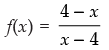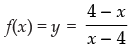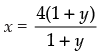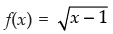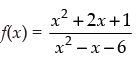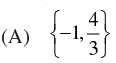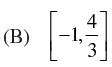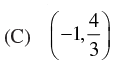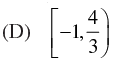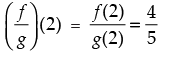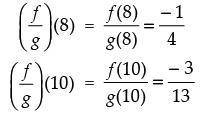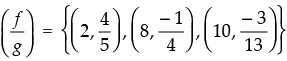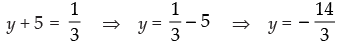Q.1. Let A = {–1, 2, 3} and B = {1, 3}. Determine
(i) A × B
(ii) B × A
(iii) B × B
(iv) A × A
Ans.
Given that: A = {- 1, 2, 3} and B = {1, 3}
(i) A × B {- 1, 2, 3} × {1, 3} = {(- 1, 1), (- 1, 3),(2, 1), (2, 3), (3, 1), (3, 3)}
(ii) B × A = {1, 3} ×{- 1, 2, 3} = {(1, - 1), (3,- 1), (1, 2), (3, 2),(1, 3), (3, 3)}
(iii) B × B = {1, 3} × {1, 3} = {(1, 1), (1, 3), (3, 1), (3, 3)}
(iv) A× A = { -1, 2, 3}× {-1, 2, 3}
= {{-1, -1), (-1,2), (-1,3),(2,-1),(2, 2),(2, 3),(3,-1),(3,2),(3,3)}
Q.2. If P = {x : x < 3, x ∈ N}, Q = {x : x ≤ 2, x ∈ W}. Find (P ∪ Q) × (P ∩ Q), where W is the set of whole numbers.
Ans.
Given that:
P = {x : x < 3, x ∈ N}
⇒ P = {1, 2}
Q = {x : x ≤ 2, x ∈W}
⇒ Q = {0, 1, 2}
Now (P ∪ Q) = {0, 1, 2} and (P ∩ Q) = {1, 2}
∴ (P ∪ Q) × (P ∩ Q) = {0, 1, 2} × {1, 2} = {(0, 1), (0, 2), (1, 1), (1, 2), (2, 1),(2, 2)}
Q.3. If A = {x : x ∈ W, x < 2} B = {x : x ∈ N, 1 < x < 5} C = {3, 5} find
(i) A × (B ∩ C)
(ii) A × (B ∪ C)
Ans.
Given that:
A = {x : x ∈ W, x < 2}
⇒ A = {0, 1}
B = {x : x ∈ N, 1 < x < 5}
⇒ B = {2, 3, 4}
⇒ C = {3, 5}
Now (B ∩ C) = {3} and (B ∪ C) = {2, 3, 4, 5}
(i) A × (B ∩ C) = {0, 1} × {3} = {(0, 3), (1, 3)}
(ii) A× (B ∪ C) = {0, 1} × {2, 3, 4, 5}
= {(0, 2), (0, 3), (0, 4), (0, 5), (1, 2), (1, 3), (1, 4), (1, 5)}
Q.4. In each of the following cases, find a and b.
(i) (2a + b, a – b) = (8, 3)
(ii) (a/4, a- 2b) = (0, 6 + b)
Ans.
(i) Given that: (2a + b, a – b) = (8, 3)
Comparing the domains and ranges, we get
2a + b = 8 ...(i)
a – b = 3 ...(ii)
Solving (i) and (ii) we get a = 11/3 and b = 2/3
(ii) Given that: (a/4, a- 2b) = (0, 6 + b)
Comparing the domains and ranges, we get
a/4 = 0 ⇒ a = 0, a – 2b = 6 + b
6 ⇒ 0 - 3b = 6 ⇒ b = - 2.
∴a = 0, b = -2.
Q.5. Given A = {1, 2, 3, 4, 5}, S = {(x, y) : x ∈ A, y ∈ A}. Find the ordered pairs which satisfy the conditions given below:
(i) x + y = 5
(ii) x + y < 5
(iii) x + y > 8
Ans.
Given that: A = {1, 2, 3, 4, 5} and
S = {(x, y) : x ∈ A, y ∈ A}
(i) x + y = 5, so, the ordered pairs satisfying the given conditions are (1, 4), (4, 1), (2, 3), (3, 2).
(ii) x + y < 5, so, the ordered pairs satisfying the given conditions are (1, 1), (1, 2), (2, 1), (1, 3), (2, 2), (3, 1).
(iii) x + y > 8, so the ordered pairs satisfying the given conditions are (4, 5), (5, 4), (5, 5).
Q.6. Given R = {(x, y) : x, y ∈ W, x2 + y2 = 25}. Find the domain and Range of R.
Ans.
Given that: R = {(x, y) : x, y ∈ W, x2 + y2 = 25} So, the ordered pairs satisfying the given condition x2 + y2 = 25 are (0, 5), (3, 4), (5, 0), (4,3) (∵ x, y ∈ W)
Hence, the domain = {0, 3, 4, 5} and the range = {0, 3, 4, 5}.
Q.7. If R1 = {(x, y) | y = 2x + 7, where x ∈ R and – 5 ≤ x ≤ 5} is a relation. Then find the domain and Range of R1.
Ans.
Given that: R1 = {(x, y)|y = 2x + 7 where x ∈ R and -5 ≤ x ≤ 5}
Since R1 is defined for all real numbers that are greater than or equal to – 5 and less than or equal to 5 ,domain of R1 is {x:– 5 ≤ x ≤ 5} = [-5, 5] Here domain is ⇒ { -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5} and y = 2x + 7.
So, the values of y for the corresponding given values of x are {-3,-1,1, 3, 5,7, 9, 11, 13, 15,17}
Hence, the domain of R1 = [-5, 5] and range of R1 = [-3, 17]
Q.8. If R2 = {(x, y) | x and y are integers and x2 + y2 = 64} is a relation. Then find R2.
Ans.
Given that: x2 + y2 = 64, x, y ∈ Z
The sum of the squares of two integers is 64
∴ For x = 0, y = ±8
For x = ±8, y = 0
Hence, R2 = {(0, 8), (0, -8), (8, 0), (-8, 0)}
Q.9. If R3 = {(x, x ) | x is a real number} is a relation. Then find domain and range of R3.
Ans.
Given that: R3 = {(x, |x|)|x is a real number}
Clearly, domain of R3 = R
and Range of R3 = (0, ∞) [∵ |x| =R+]
Q.10. Is the given relation a function? Give reasons for your answer.
(i) h = {(4, 6), (3, 9), (– 11, 6), (3, 11)}
(ii) f = {(x, x) | x is a real number}
(iii) g = n, 1/n, |n is a positive integer n
(iv) s = {(n, n2) | n is a positive integer}
(v) t = {(x, 3) | x is a real number.
Ans.
Given that: (i) h = {(4, 6), (3, 9), (– 11, 6), (3, 11)} Since in the given relation 3 has two images 9 and 11. So, h is not a function.
(ii) f = {(x, x)|x is a real number}. Here, we observe that for every element of domain has a unique image. So, f is a function.
(iii) Given that:
g = n, 1/n |n is a positive integer
Here, we observe that n is a positive integer so, for every element of domain, there is a unique 1/n image. Hence g is a function.
(iv) Given that: S = {(n, n2)|n is a positive integer} Here, we observe that the square of any integer is a unique number. So, for every element element in the domain there is unique image. Hence, S is a function.
(v) Given that: t = {(x, 3)|x is a real number} Here, we observe that for every real element in the domain, there is a constant number 3. Hence t is a constant function.
Q.11. If f and g are real functions defined by f (x) = x2 + 7 and g (x) = 3x + 5, find each of the following
(a) f (3) + g (– 5)
(b) f(1/2) × g(14)
(c) f (– 2) + g (– 1)
(d) f (t) – f (– 2)
(e) f(t) - f(5)/t-5, if t ≠ 5
Ans.
Given that: f(x) = x2 + 7 and g(x) = 3x + 5
(i) f(3) + g(– 5) = [(3)2 + 7] + [3(– 5) + 5]
= (9 + 7) + (– 15 + 5) = 16 – 10 = 6
Hence, f(3) + g(– 5) = 6
(ii)
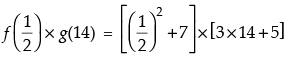
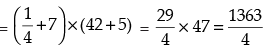
Hence, 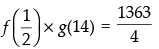
(iii) f(– 2) + g(– 1) = [(– 2)2 + 7] + [3(– 1) + 5] = (4 + 7) + (– 3 + 5) = 11 + 2 = 13
Hence, f(– 2) + g(– 1) = 13
(iv) f(t) – f(– 2) = (t2 + 7) – [(– 2)2 + 7] = t2 + 7 – 11 = t2 – 4
Hence, f(t) – f(– 2) = t2 – 4.
(v)
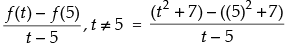
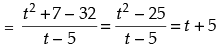
Hence, 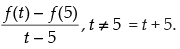
Q.12. Let f and g be real functions defined by f (x) = 2x + 1 and g (x) = 4x – 7.
(a) For what real numbers x, f (x) = g (x)?
(b) For what real numbers x, f (x) < g (x)?
Ans.
Given that: f(x)= 2x + 1 and g(x) = 4x – 7
(i) For f(x) = g(x), we get
2x + 1 = 4x – 7
⇒ 2x – 4x = -7 – 1 ⇒
- 2x = - 8
⇒ x = 4.
Hence,the required real number is 4.
(ii) For f(x) < g(x), we get
2x + 1 < 4x – 7
⇒ 2x – 4x < - 1 – 7
⇒-2x <- 8
⇒ 2x >8
∴ x >4
Hence, the required real number is x > 4.
Q.13. If f and g are two real valued functions defined as f (x) = 2x + 1, g (x) = x2 + 1, then find.
(i) f + g
(ii) f – g
(iii) f.g
(iv) f/g
Ans.
Given that: f(x) = 2x + 1 and g(x) = x2 + 1
(i) f + g = f(x) + g(x)
⇒ 2x + 1 +x2 + 1
⇒ x2 + 2x + 2
(ii) f – g = f(x) – g(x)
⇒ (2x + 1) – (x2 + 1)
= 2x +1 – x2 – 1
⇒ 2x – x2
(iii) f.g = f(x).g(x)
⇒ (2x + 1) (x2 + 1)
⇒ 2x3 + x2 + 2x + 1
(iv) f/g = f(x)/g(x) = 2x + 1/x2 + 1
Q.14. Express the following functions as set of ordered pairs and determine their range. f : X → R, f (x) = x3 + 1, where X = {–1, 0, 3, 9, 7}
Ans.
Given that: f : X → R, f(x) = x3 + 1, where X = {-1, 0, 3, 9, 7}
Here X = {-1, 0, 3, 9, 7}
For x = -1, f(-1) = (-1)3 + 1 = 0
For x = 0, f(0) = (0)3 + 1 = 1
For x = 3, f(3) = (3)3 + 1 = 28
For x = 9, f(9) = (9)3 + 1 = 730
For x = 7, f(7) = (7)3 + 1 = 344
∴ The ordered pairs are (-1, 0), (0, 1), (3, 28), (7, 344), (9, 730) and the range = {0, 1, 28, 344, 730}.
Q.15. Find the values of x for which the functions f (x) = 3x2 – 1 and g (x) = 3 + x are equal?
Ans.
Given that: f(x) = 3x2 – 1 and g(x) = 3 + x
Since f(x) = g(x) (given)
⇒ 3x2 – 1 = 3 + x
⇒ 3x2 – x – 4 = 0
⇒ 3x2 – 4x + 3x – 4 = 0
⇒ x(3x – 4) + 1(3x – 4) = 0
⇒ (3x – 4)(x + 1) = 0
⇒ 3x – 4 = 0 or x + 1 = 0
⇒ 3x = 4 or x = – 1
∴ x = 4/3
Hence, the value of x are – 1 and 4/3.
Long Answer Type
Q.16. Is g = {(1, 1), (2, 3), (3, 5), (4, 7)} a function? Justify. If this is described by the relation, g (x) = αx + β, then what values should be assigned to α and β?
Ans.
Given that: g = {(1, 1), (2, 3), (3, 5), (4, 7)}
Since every element of the domain in this relations has unique image, so g is a function.
Now g(x) = αx + β
For (1, 1) g(1) = α (1) + β = 1 ⇒ α + β = 1 ...(i)
For (2, 3) g(2) = α(2) + β = 3⇒ 2α + β = 3 ...(ii)
Solving eqn. (i) and (ii) we have
α= 2 and β = -1
[Note: We can take any other two ordered pairs]
Hence, the value of α= 2 and β = -1.
Q.17. Find the domain of each of the following functions given by
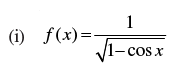

(iii) f(x) = x |x|
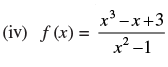
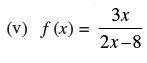
Ans.
(i) Given that: f(x)
= 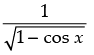
We know that – 1 cos ≤ x ≤ 1
⇒1 ≥ - cos x ≥ - 1
⇒ 1 + 1 ≥ 1 – cos x ≥ -1 + 1
⇒ 2 ≥ 1 – cos x ≥ 0
⇒ 0 ≤ 1 – cos x ≤ 2
For real value of domain
1 – cos x ≠ 0 ⇒ cos x ≠ 1
⇒ x ≠ 2nπ ∀ n ∈ Z
Hence, the domain of f = R – {2nπ, n ∈ Z}
(ii) Given that:
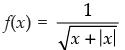
∵ x + |x| = x + x = 2x if x ≥ 0
and x + |x|= x – x = 0 if x < 0
So far x < 0, f is not defined.
Hence, the domain f = R+.
(iii) Given that: f(x) = x|x|
It is clear that f(x) is defined for all x ∈ R.
Hence, the domain of f = R.
(iv) Given that:
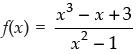
Here, f(x) is only defined if x2 -1 ≠ 0
(x–1)(x+1) ≠ 0
∴ x ≠ 1, x ≠ - 1
Hence, the domain of f = R – {-1, 1}
(v) Given that:

Here, f(x) is only defined if 28– x ≠ 0 ⇒ x ≠ 28
Hence, the domain = R – {28}.
Q.18. Find the range of the following functions given by
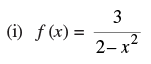
(ii) f(x) = 1 - |x-2|
(iii) f(x) = |x – 3|
(iv) f(x)= 1 + 3 cos 2x
Ans.
(i) Given that:
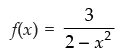
Let y = f(x)
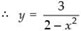
⇒ y(2– x2) = 3
⇒ 2y – yx2 = 3
⇒ yx2 = 2y – 3

Here, x is real if 2y – 3 ≥ 0 and y ≥ 0
⇒ 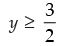
Hence, the range of f =

(ii) Given that: f(x) = 1 - |x – 2|
We know that |x – 2|= - (x – 2) if x < 2
and |x– 2|= (x–2), x ≥ 2
∴ -|x– 2| ≤ 0
⇒ 1 - |x – 2|≤ 1
Hence, the range of f = (-∞, 1].
(iii) Given that: f(x) = |x – 3|
We know that |x – 3| ≥ 0
⇒ f(x) ≥ 0
Hence, the range of f = [0, ∞)
(iv) Given that: f(x) = 1 + 3 cos 2x
We know that – 1 ≤ cos 2x ≤ 1
⇒ -3 ≤ 3 cos 2x ≤ 3
⇒- 3 + 1 ≤ 1 + 3 cos 2x ≤ 3 + 1
⇒ -2 ≤ 1 + 3 cos 2x ≤ 4
⇒- 2 ≤ f(x) ≤ 4
Hence, the range of f = [- 2, 4].
Q.19. Redefine the function f (x) = x − 2 + 2 + x , – 3 ≤ x ≤ 3.
Ans.
Given that: f(x) = |x – 2| + |2 + x|, - 3 ≤ x ≤ 3
Since |x – 2| = - (x – 2), x < 2
and |x– 2| = (x – 2), x ≥ 2
|2+ x| =- (2 + x), x < - 2
|2+x| = (2+ x), x ≥ - 2
Now f(x) = |x–2|+ |2 +x|, - 3 ≤x ≤ 3.
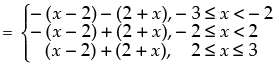
∴ 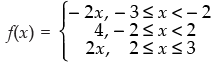
f(x) = 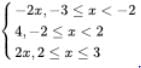
Q.20. If f (x) = x - 1/x + 1, then show that
Ans.
Given that:
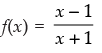
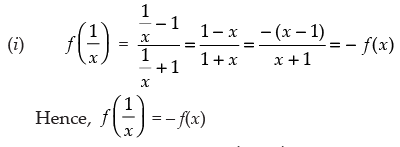
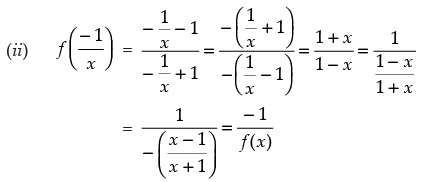
Hence,
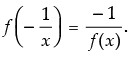
Q.21. Let f (x) = √x and g (x) = x be two functions defined in the domain R+ ∪ {0}.Find
(i) (f + g) (x)
(ii) (f – g) (x)
(iii) (fg) (x)
(iv) (f/g) (x)
Ans.
Given that: f(x) = √x and g(x) = x be two functions defined in the domain R+ ∪ {0}
(i) (f + g)(x) = f(x) + g(x) = √x + x
(ii) (f – g)(x) = f(x) – g(x) = √x - x
(iii) (fg)(x) = f(x).g(x) = √x . x = x 3/2
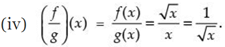
Q.22. Find the domain and Range of the function f (x),
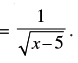
Ans.
Given that:
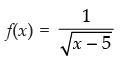
Here, it is clear that f(x) is real when x – 5 > 0 ⇒ x > 5
Hence, the domain = (5, ∞)
Now to find the range put
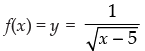
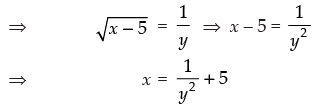
For x ∈ (5, ∞), y ∈ R+.
Hence, the range of f = R+.
Q.23. If f (x) = y = ax - b/cx - a, then prove that f (y) = x.
Ans.
Given that:f(x) = y
= 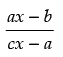
putting x = y in f(x) we get
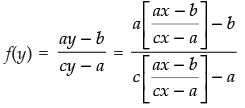
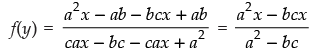
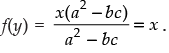
Hence, f(y) = x.
Objective Type Questions
Q.24. Let n (A) = m, and n (B) = n. Then the total number of non-empty relations that can be defined from A to B is
(a) mn
(b) nm – 1
(c) mn – 1
(d) 2mn – 1
Ans. (d)
Solution.
Given that: n(A) = m and n(B) = n
∴ n(A × B) = n(A) . n(B) = mn
So, the total number of relations from A to B 2mn – 1.
Hence, the correct option is (d)
Q.25. If [x]2 – 5 [x] + 6 = 0, where [ . ] denote the greatest integer function, then
(a) x ∈ [3, 4]
(b) x ∈ (2, 3]
(c) x ∈ [2, 3]
(d) x ∈ [2, 4)
Ans. (c)
Solution.
we have [x]2 – 5[x] + 6 = 0
⇒ [x]2 – 3[x] 2[x] + 6 = 0
⇒ [x]([x]– 3)–2([x]–3)= 0
⇒ ([x]– 3)([x]–2) =0
⇒ [x] = 2, 3
So, x ∈ [2, 3].
Hence, the correct option is (c).
Q.26. Range of f (x) = 1/1-2 cos x is
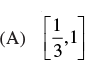
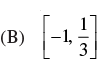
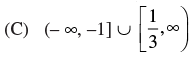
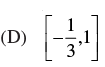
Ans. (b)
Solution.
Given that:
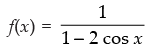
We know that – 1 ≥ cos x ≤ 1
⇒ 1 ≥ cos x ≥ - 1
⇒ - 1 ≤ - cos x ≤1
⇒ -2 ≤ - 2 cos x ≤ 2
⇒- 2+ 1 ≤ 1– 2 cos x ≤ 2 +1
⇒ -1 ≤ 1 – 2 cos x ≤ 3
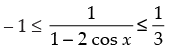
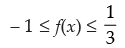
So the range of f(x) = [-1, 1/3]
Hence, the correct option is (b).
Q.27. Let  , then
, then
(a) f (xy) = f (x) . f (y)
(b) f (xy) ≥ f (x) . f (y)
(c) f (xy) ≤ f (x) . f (y)
(d) None of these
[Hint : find f (xy) =  f (x) . f (y) = 1+
f (x) . f (y) = 1+  ]
]
Ans. (c)
Solution.
Given that:
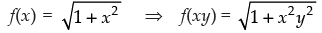
and f(x) . f(y)
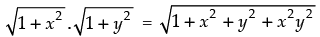
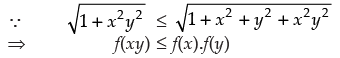
Hence, the correct option is (c).
Q.28. Domain of √a2 - x2 (a>0) is
(a) (– a, a)
(b) [– a, a]
(c) [0, a]
(d) (– a, 0]
Ans. (b)
Solution.
Let
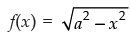
f(x) is defined if a2 – x2 ≥ 0
⇒ x2 – a2 ≤ 0
⇒ x2 ≤ a2
⇒ x ≤ ±a
⇒ -a≤x ≤ a
∴ Domain of f(x) = [-a, a]
Hence, the correct option is (b).
Q.29. If f (x) = ax + b, where a and b are integers, f (–1) = – 5 and f (3) = 3, then a and b are equal to
(a) a = – 3, b = –1
(b) a = 2, b = – 3
(c) a = 0, b = 2
(d) a = 2, b = 3
Ans. (b)
Solution.
Given that: f(x) = ax+ b
⇒ f(-1) = a(-1) +b
⇒ - 5 = - a+b
⇒ a – b = 5 ….(i)
f(3) =3a + b
⇒ 3 = 3a + b
⇒ 3a + b = 3…..(ii)
On solving eqn. (i) and (ii), we get a = 2, b = - 3
Hence, the correct option is (b).
Q.30. The domain and range of the real function f defined by f (x) = 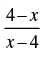
is given by
(A) Domain = R, Range = {–1, 1}
(B) Domain = R – {1}, Range = R
(C) Domain = R – {4}, Range = {– 1}
(D) Domain = R – {– 4}, Range = {–1, 1}
Ans. (a)
Solution.
Given that:
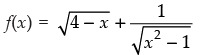
f(x) is defined if
4– x ≥ 0 or x2 – 1 > 0
⇒ - x ≥ - 4 or (x – 1)(x + 1) >0
⇒ x ≤ 4 or x < - 1 and x > 1
∴ Domain of f(x) is (- ∞, - 1) ∪ (1, 4]
Hence, the correct option is (a).
Q.31. The domain and range of the real function f defined by f (x) = 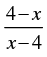
is given by
(a) Domain = R, Range = {–1, 1}
(b) Domain = R – {1}, Range = R
(c) Domain = R – {4}, Range = {– 1}
(d) Domain = R – {– 4}, Range = {–1, 1}
Ans. (c)
Solution.
Given that:
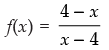
We know that f(x) is defined if x – 4≠ 0⇒x≠4
So,the domain of f(x) is = R – {4}
Let,
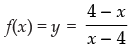
⇒ yx – 4y = 4 – x
⇒ yx + x = 4y + 4
⇒ x(y + 1) = 4y + 4
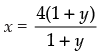
If x is real number, then 1 + y ≠ 0 ⇒ x ≠1
∴ Range of f(x) = R–{ -1)
Hence, the correct option is (c).
Q.32. The domain and range of real function f defined by f (x) = √x - 1
is given by
(a) Domain = (1, ∞), Range = (0, ∞)
(b) Domain = [1, ∞), Range = (0, ∞)
(c) Domain = [1, ∞), Range = [0, ∞)
(d) Domain = [1, ∞), Range = [0, ∞)
Ans. (d)
Solution.
Given that:
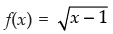
f(x) is defined if x – 1 ≥ 0 ⇒ x ≥ 1
∴ Domain of f(x) = [0, ∞)
Let f(x) = y = √x - 1
⇒ y2 = x – 1
⇒ x = y2 + 1
If x is real then y ∈ R
∴ Range of f(x) = [0, ∞)
Hence, the correct option is (d).
Q.33. The domain of the function f given by f(x) = x2 + 2x + 1/x2 - x - 6 is
(a) R – {3, – 2}
(b) R – {–3, 2}
(c) R – [3, – 2]
(d) R – (3, – 2)
Ans. (a)
Solution.
Given that:
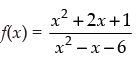
F(x) is defined if x2 – x – 6 ≠ 0
⇒ x2 – 3x + 2x– 6≠0
⇒ (x– 3)(x + 2) ≠0
⇒ x ≠ - 2, x ≠ 3
So, the domain of f(x) = R – {-2, 3}
Hence, the correct option is (a).
Q.34. The domain and range of the function f given by f (x) = 2 – x − 5 is
(a) Domain = R+, Range = ( – ∞, 1]
(b) Domain = R, Range = ( – ∞, 2]
(c) Domain = R, Range = (– ∞, 2)
(d) Domain = R+, Range = (– ∞, 2]
Ans. (b)
Solution.
Given that: f(x) = 2 – |x– 5|
Here, f(x) is defined for x ∈ R
∴ Domain of f(x) = R
Now,|x– 5|≥0
⇒ -|x – 5|≤0
⇒ 2-|x– 5|≤2
⇒ f(x) ≤ 2
∴ Range of f(x) = (- ∞, 2]
Hence, the correct option is (b).
Q.35. The domain for which the functions defined by f (x) = 3x2 – 1 and g (x) = 3 + x are equal is
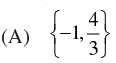
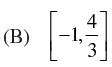
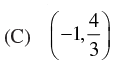
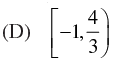
Ans.
Given that: f(x) = 3x2 – 1 and g(x) = 3 + x
f(x) = g(x)
⇒ 3x2 – 1 = 3 + x
⇒ 3x2 – x – 4 = 0
⇒ 3x2 – 4x + 3x – 4 = 0
⇒ x(3x – 4) + 1(3x – 4)= 0
⇒ (x+1)(3x–4)= 0
⇒ x + 1 = 0 or 3x – 4 = 0
⇒ x = - 1, or x = 4/3
∴ Domain = {-1, 4/3}
Hence, the correct option is (a).
Fill in the blanks:
Q.36. Let f and g be two real functions given by
f = {(0, 1), (2, 0), (3, – 4), (4, 2), (5, 1)}
g = {(1, 0), (2, 2), (3, – 1), (4, 4), (5, 3)}
then the domain of f . g is given by _______.
Ans.
Given that: f(x) = {(0, 1), (2, 0), (3, – 4), (4, 2), (5, 1)}
and g(x) = {(1, 0), (2, 2), (3, – 1), (4, 4), (5, 3)}
∴ Domain of f = {0, 2, 3, 4, 5}
and domain of g = {1, 2, 3, 4, 5}
So, domain of f.g = Domain of f ∩ Domain of g = {2, 3, 4, 5}
Hence, the filler is {2, 3, 4, 5}.
Q.37. Let f = {(2, 4), (5, 6), (8, – 1), (10, – 3)}
g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, 5)}
be two real functions. Then Match the following:

Ans.
Given that: f = {(2, 4), (5, 6), (8, – 1), (10, – 3)}
and g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, 5)}
f – g, f + g, f.g, f/g are defined in the domain
(domain of f ∩ domain of g)
(i) (f – g)2= f(2) – g(2) = 4 – 5 = - 1
(f – g)8 = f(8) – g(8) = - 1 – 4 = - 5
(f – g)10 = f(10) – g(10) = - 3 – 13 = - 16
∴ (f – g) = {(2, - 1), (8, - 5), (10, - 16)}
(ii) (f + g)2 = f(2) + g(2) = 4 + 5 = 9
(f + g)8 = f(8) + g(8) = – 1 + 4 = 3
(f + g)10 = f(10) + g(10) = – 3 + 13 = 10
∴ (f + g) = {(2, 9), (8, 3), (10, 10)}
(iii) (f . g)2 = f(2). g(2) = 4. 5 = 20
(f . g)8 = f(8) . g(8) = (- 1). (4)= - 4
(f . g)10 = f(10) . g(10)= - 3. 13 = - 39
∴ (f . g) = {(2, 20), (8,- 4), (10, - 39)}
(iv)
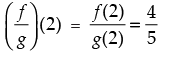
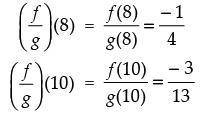
∴ 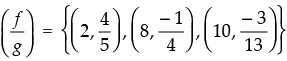
Hence, the correct option is
(a) ↔ (iii)
(b) ↔ (iv)
(c) ↔ (ii)
(d) ↔ (i)
State True or False for the following statements
Q.38. The ordered pair (5, 2) belongs to the relation R = {(x, y) : y = x – 5, x, y ∈ Z}
Ans.
Given that: R = {(x, y) : y = x – 5, x, y ∈ Z}
For (5, 2), y = x – 5
Put x = 5, y = 5 – 5 = 0 ≠ 2
So (5, 2) is not the ordered pair of R.
Hence, the statement is ‘False’.
Q.39. If P = {1, 2}, then P × P × P = {(1, 1, 1), (2, 2, 2), (1, 2, 2), (2, 1, 1)}
Ans.
Given that P = {1, 2}
∴ P × P = {1, 2} ´ {1, 2} = {(1, 1), (1, 2), (2, 1), (2, 2)}
P × P × P = {(1, 1), (1, 2), (2, 1), (2, 2)} × {1, 2}
= {(1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2)}
So, given statement is ‘False’.
Q.40. If A = {1, 2, 3}, B = {3, 4} and C = {4, 5, 6}, then (A × B) ∪ (A × C) = {(1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6)}.
Ans.
Given that: A = {1, 2, 3}, B = {3, 4} and C = {4, 5, 6}
A × B = {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}
And A × C = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
(A × B) ∪ (A × C) = {(1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5),
(2, 6), (3, 3), (3, 4), (3, 5), (3, 6)}
Hence, the given statement is ‘True’.
Q.41. If (x – 2, y + 5) = (-2, 1/3) are two equal ordered pairs, then x = 4, y = -14/3
Ans.
Given that: (x – 2, y + 5) = (-2, 1/3)
⇒ x – 2 = – 2
⇒ x = 0
and
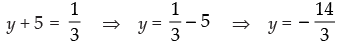
Hence, the given statement is ‘False’.
Q.42. If A × B = {(a, x), (a, y), (b, x), (b, y)}, then A = {a, b}, B = {x, y}
Ans.
Given that: A = {a, b} and B = {x, y}
∴ A × B = {(a, x), (a, y), (b, x), (b, y)}
Hence, the statement is ‘True’.
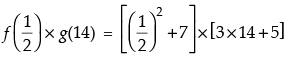
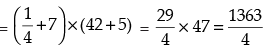
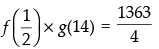
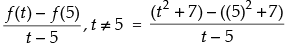
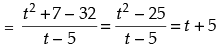
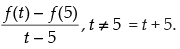
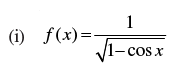

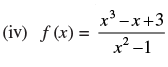
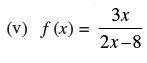
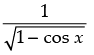
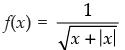
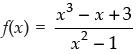

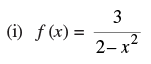
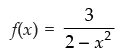
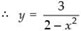

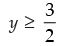

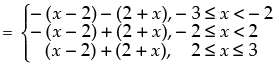
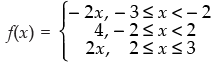
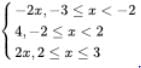
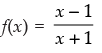
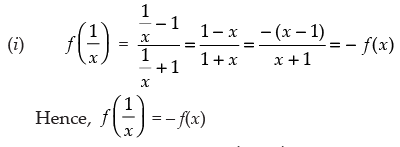
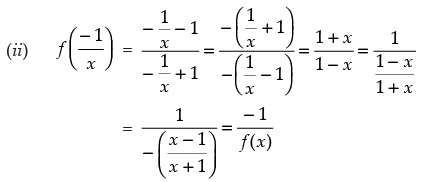
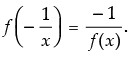
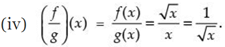
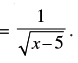
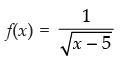
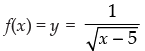
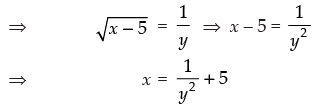
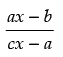
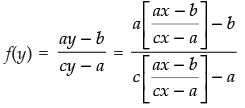
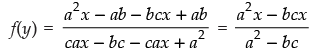
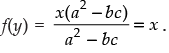
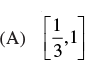
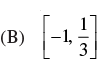
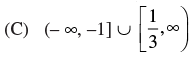
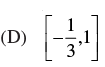
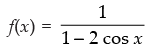
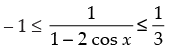
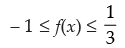
 , then
, then f (x) . f (y) = 1+
f (x) . f (y) = 1+  ]
]