Class 7 Maths Chapter 2 Question Answers - Linear Equations in One Variable
Ques 1: Show that x = 4 is a solution of the equation:
Solution: Substituting x = 4 in 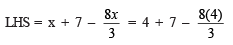
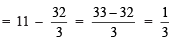
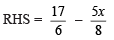

Since, LHS = RHS
∴ x = 4 is a solution of the given equation.
Ques 2: Solve
Solution: We have 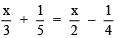
LCM of 3, 5, 2 and 4 is 60.
∴ The given equation can be expressed as:
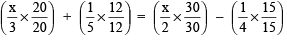
⇒ 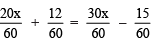
⇒ 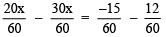
⇒ 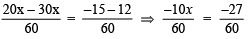
⇒ 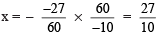
Thus, x = 27/10 is the required solution.
Ques 3: Solve for
Solution: We have 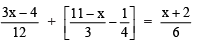
⇒ 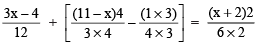
⇒ 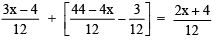
⇒ 3x – 4 + 44 – 4x – 3 = 2x + 4
⇒ 3x – 4x – 2x = 4 + 3 – 44 + 4
⇒ 3x – 6x = 11 – 44
⇒ –3x = –33 ⇒ x = 11
Ques 4: Solve for
Solution: We have
By cross multiplication, we get:
(2 + x)(7 – x) = (5 – x)(4 + x)
⇒ 2(7 – x) + x(7 – x) = 5(4 + x) – x(4 + x)
⇒ 14 – 2x + 7x – x2 = 20 + 5x – 4x – x2
⇒ –x2 + x2 – 2x + 7x – 5x + 4x = 20 – 14
⇒ –7x + 7x + 4x = 6
⇒ 4x = 6 ⇒ x = 6/4 or 3/2
Thus, the solution of the given equation is x = 3/2
Ques 5: A number is such that it is as much greater than 65 as it is less than 91. Find the number.
Solution: Let the number be x.
Since, we have [The number] – 65 = 91 – [The number]
⇒ x – 65 = 91 – x
⇒ x + x = 91 + 65
⇒ 2x = 156
⇒ x = 156/2 = 78
Thus, the required number is 78.
Ques 6: The numerator of a fraction is 2 less than the denominator. If 1 is added to its denominator, it becomes 1/2. Find the fraction.
Solution: Let the denominator of the fraction be x.
∴ Numerator = x – 2
The fraction =
Since it becomes 1/2
When 1 is added to its denominator.
i.e
By cross multiplication, we have
2(x – 2) = x + 1
⇒ 2x – 4 = x + 1
⇒ 2x – x = 1 + 4
⇒ x = 5
⇒ Fraction =
Ques 7: After 24 years I shall be 3 times as old as I was 4 years ago. Find my present age.
Solution: Let my present age be x years.
∴ After 24 years, my age will be (x + 24) years.
4 years ago, my age was (x – 4) years.
According to the given condition, we have
(x + 24) = 3(x – 4)
⇒ x + 24 = 3x – 12
⇒ x – 3x = –12 – 24
⇒ –2x = –36
⇒ x = -36/-2 = 18
Thus, my present age is 18 years.
Ques 8: If the sum of two numbers is 30 and their ratio is 2 : 3, then find the numbers.
Solution: Let one of the numbers be x.
∴ The other number = (30 – x)
According to the condition, we have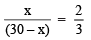 [∵ The ratio number is 2 : 3]
[∵ The ratio number is 2 : 3]
⇒ 3x = 2(30 – x) [By cross multiplication]
⇒ 3x = 60 – 2x
⇒ 3x + 2x = 60
⇒ 5x = 60
⇒ x = 60/5 = 12
∴ 30 – x = 30 – 12 = 18
Thus, the required numbers are 12 and 18.
|
81 videos|452 docs|31 tests
|
FAQs on Class 7 Maths Chapter 2 Question Answers - Linear Equations in One Variable
| 1. What are linear equations in one variable? |  |
| 2. How can I solve a linear equation in one variable? |  |
| 3. What is the importance of solving linear equations in one variable? |  |
| 4. Can linear equations have more than one solution? |  |
| 5. What is the significance of the slope-intercept form of a linear equation? |  |

















