RD Sharma Solutions Ex-4.1, Algebraic Identities, Class 9, Maths | RD Sharma Solutions for Class 9 Mathematics PDF Download
Q. 1. Evaluate each of the following using identities:
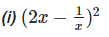
Solution:
Given,
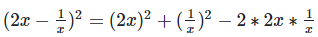
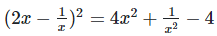[?(a−b)2 = a2+b2−2ab]
Where, a = 2x, b = 1/x
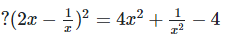
(ii) (2x+y) (2x-y)
Solution:
Given, (2x+y) (2x-y)
= (2x)2−(y)2[?(a+b)(a−b) = a2−b2]
= 4x2−y2
?(2x+y)(2x−y) = 4x2−y2
(iii) (a2b−ab2)2
Given, (a2b−ab2)2
= (a2b)2+(ab2)2−2∗a2b∗ab2 [?(a−b)2 = a2+b2−2ab]
Where, a = a2b,b = ab2
= a4b2+b4a2−2a3b3
?(a2b−ab2)2 = a4b2+b4a2−2a3b3
(iv) (a-0.1) (a+0.1)
Solution:
Given, (a-0.1) (a+0.1)
= a2−(0.1)2[?(a+b)(a−b) = a2−b2]
Where, a = a and b = 0.1
= a2−0.01
?(a−0.1)(a+0.1) = a2−0.01
(v) (1.5x2−0.3y2)(1.5x2+0.3y2)
Solution:
Given, (1.5x2−0.3y2)(1.5x2+0.3y2)
= (1.5x2)2−(0.3y2)2 [?(a+b)(a−b) = a2−b2]
Where, a = 1.5x2,b = 0.3y2
= 2.25x4−0.09y4
?(1.5x2−0.3y2)(1.5x2+0.3y2) = 2.25x4−0.09y4
Q.2. Evaluate each of the following using identities:
(i) (399)2
Solution:
We have,
3992 = (400-1)2
= (400)2+(1)2 – 2x400x1 [ (a-b)2 = a2+ b2-2ab ]
Where, a = 400 and b = 1
= 160000 + 1 – 8000
= 159201
Therefore, (399)2 = 159201.
(ii) (0.98)2
Solution:
We have,
(0.98)2 = (1-0.02)2
= (1)2 + (0.02)2 – 2x1x0.02
= 1 + 0.0004 – 0.04 [ Where, a=1 and b=0.02 ]
= 1.0004 – 0.04
= 0.9604
Therefore, (0.98)2 = 0.9604
(iii) 991x1009
Solution:
We have,
991x1009
= (1000-9) (1000+9)
= (1000)2 – (9)2 [ (a+b) (a-b) = a2 – b2 ]
= 1000000 – 81 [ Where a=1000 and b=9 ]
= 999919
Therefore, 991x1009 = 999919
(iv) 117x83
Solution:
We have,
117x83
= (100+17) (100-17)
= (100)2 – (17)2 [ (a+b) (a-b) = a2 – b2 ]
= 10000 – 289 [ Where a=100 and b=17 ]
= 9711
Therefore, 117x83 = 9711
Q.3. Simplify each of the following:
(i) 175 x 175 +2 x 175 x 25 + 25 x 25
Solution:
We have,
175 x 175 +2 x 175 x 25 + 25 x 25 = (175)2 + 2 (175) (25) + (25)2
= (175+25)2 [ a2+ b2+2ab = (a+b)2 ]
= (200)2 [ Where a=175 and b=25 ]
= 40000
Therefore, 175 x 175 +2 x 175 x 25 + 25 x 25 = 40000.
(ii) 322 x 322 – 2 x 322 x 22 + 22 x 22
Solution:
We have,
322 x 322 – 2 x 322 x 22 + 22 x 22
= (322-22)2 [ a2+ b2-2ab = (a-b)2 ]
= (300)2 [ Where a=322 and b=22 ]
= 90000
Therefore, 322 x 322 – 2 x 322 x 22 + 22 x 22= 90000.
(iii) 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24
Solution:
We have,
0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24
= (0.76+0.24)2 [ a2+ b2+2ab = (a+b)2 ]
= (1.00)2 [ Where a=0.76 and b=0.24 ]
= 1
Therefore, 0.76 x 0.76 + 2 x 0.76 x 0.24 + 0.24 x 0.24 = 1.
(iv)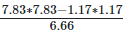 
Solution:
We have,
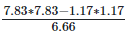
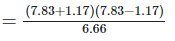[?(a−b)2 = (a+b)(a−b)]
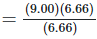
= 9
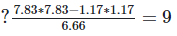
Q.4. If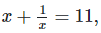 
,find the value of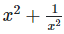
Solution:
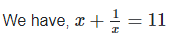
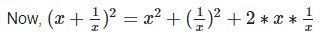
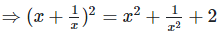
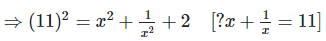
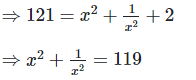
Q.5. If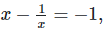 
,find the value of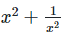
Solution: We have,
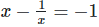
Now,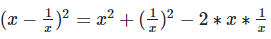 
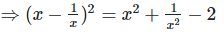
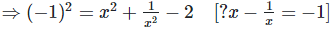
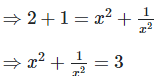
Q. 6. If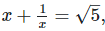 
find the value of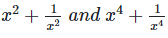 
Solution:
We have,
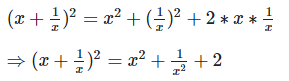
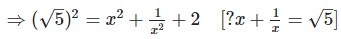
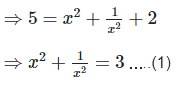
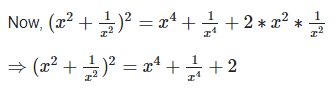
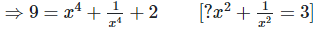
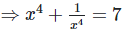
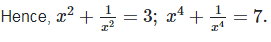
Q. 7. If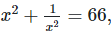 
find the value of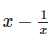
Solution:
We have,
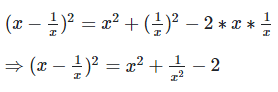
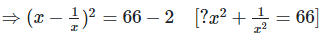
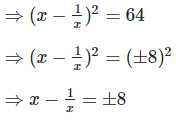
Q. 8. If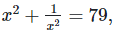 
find the value of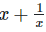 
Solution:
We have,
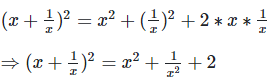
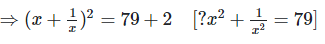
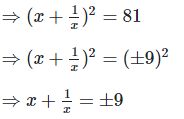
Q. 9. If 9x2 + 25y2 = 181 and xy = -6, find the value of 3x + 5y.
Solution:
We have,
(3x + 5y)2 = (3x)2 + (5y)2 + 2*3x*5y
⇒(3x + 5y)2 = 9x2 + 25y2 + 30xy
= 181 + 30(-6) [Since, 9x2 + 25y2 = 181 and xy = -6]
⇒ (3x+5y)2 = 1
⇒ (3x+5y)2 = (±1)2
⇒ 3x+5y = ±1
Q.10. If 2x + 3y = 8 and xy = 2, find the value of 4x2 + 9y2.
Solution:
We have,
(2x + 3y)2 = (2x)2 + (3y)2 + 2*2x*3y
⇒ (2x + 3y)2 = 4x2 + 9y2 + 12xy [Since, 2x + 3y = 8 and xy = 24 ]
⇒ (8)2 = 4x2 + 9y2 + 24
⇒ 64 – 24 = 4x2 + 9y2
⇒ 4x2 + 9y2 = 40
Q. 11. If 3x - 7y = 10 and xy = -1, find the value of 9x2 + 49y2.
Solution:
We have,
(2 - 7y)2 = (3x)2 + (-7y)2 - 2*3x*7y
⇒ (3x - 7y)2 = 9x2 + 49y2 - 42xy [Since, 3x - 7y = 10 and xy = -1 ]
⇒ (10)2 = 9x2 + 49y2 + 42
⇒ 100 – 42 = 9x2 + 49y2
⇒ 9x2 + 49y2 = 58
Q.12. Simplify each of the following products:
(i)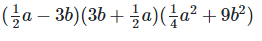 
Solution:
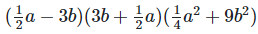
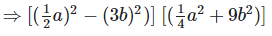
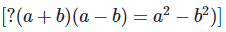
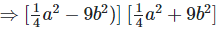
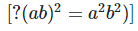
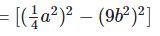
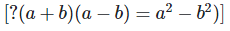
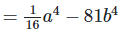
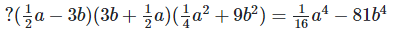
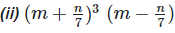
Solution:
We have,
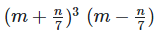
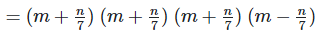
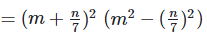[?(a+b)(a+b) = (a+b)2 and (a+b)(a−b) = a2−b2]
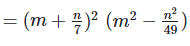
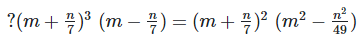
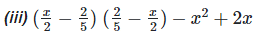
Solution:
We have,
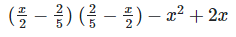
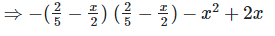
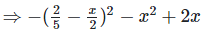[?(a−b)(a−b) = (a−b)2]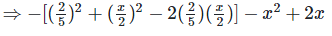
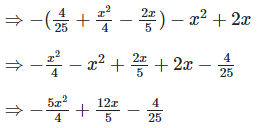
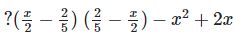
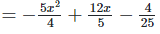
(iv) (x2+x−2)(x2−x+2)
Solution:
(x2+x−2)(x2−x+2)
[(x)2+(x−2)][(x2−(x+2)]
⇒ (x2)2−(x−2)2 [(a – b) (a + b) = a2 - b2]
⇒ x4−(x2+4−4x)[?(a−b)2 = a2+b2−2ab]
⇒ x4−x2+4x−4
?(x2+x−2)(x2−x+2) = x4−x2+4x−4
(v) (x3−3x−x)(x2−3x+1)
Solution:
We have,
(x3−3x−x)(x2−3x+1)
⇒ x(x2−3x−1)(x2−3x+1)
⇒ x[(x2−3x)2−(1)2][?(a+b)(a−b) = a2−b2]
⇒ x[(x2)2+(−3x)2−2(3x)(x2)−1]
⇒ x[x4+9x2−6x3−1]
⇒ x5−6x4+9x3−x
?(x3−3x−x)(x2−3x+1) = x5−6x4+9x3−x
(vi) (2x4−4x2+1)(2x4−4x2−1)
Solution:
We have,
(2x4−4x2+1)(2x4−4x2−1)
⇒ [(2x4−4x2)2−(1)2] [?(a+b)(a−b) = a2−b2]
⇒ [(2x4)2+(4x2)2−2(2x4)(4x2)−1]
⇒ 4x8−16x6+16x4−1 [?(a−b)2 = a2+b2−2ab]
?(2x4−4x2+1)(2x4−4x2−1) = 4x8−16x6+16x4−1
Q.13. Prove that a2+b2+c2−ab−bc−ca is always non-negative for all values of a, b and c.
Solution:
We have,
a2+b2+c2−ab−bc−ca
Multiply and divide by ‘2’
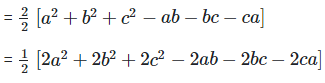
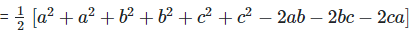
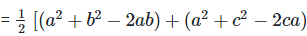
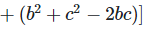
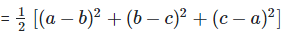
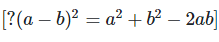
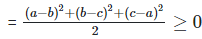
?a2+b2+c2−ab−bc−ca ≥ 0
Hence, a2+b2+c2−ab−bc−ca ≥ 0 is always non-negative for all values of a, b and c.
FAQs on RD Sharma Solutions Ex-4.1, Algebraic Identities, Class 9, Maths - RD Sharma Solutions for Class 9 Mathematics
| 1. What are algebraic identities? |  |
| 2. How can algebraic identities be used to solve equations? | |
| 3. Can you provide an example of how to use algebraic identities to solve an equation? | |
| 4. Are there any specific rules to remember while using algebraic identities? | |
| 5. Can algebraic identities be used in real-life applications? | |
|
4.77/5 Rating |
|
Nov 23, 2024 Last updated |
|
Explore Courses for Class 9 exam
|
|
Algebraic Identities
,Free
,video lectures
,study material
,Objective type Questions
,shortcuts and tricks
,RD Sharma Solutions Ex-4.1
,mock tests for examination
,MCQs
,Maths | RD Sharma Solutions for Class 9 Mathematics
,Maths | RD Sharma Solutions for Class 9 Mathematics
,RD Sharma Solutions Ex-4.1
,Algebraic Identities
,Viva Questions
,Maths | RD Sharma Solutions for Class 9 Mathematics
,Important questions
,Class 9
,ppt
,Extra Questions
,practice quizzes
,Sample Paper
,Semester Notes
,Exam
,Algebraic Identities
,Class 9
,Previous Year Questions with Solutions
,past year papers
,RD Sharma Solutions Ex-4.1
,Class 9
,Summary
;
RD Sharma Solutions Ex-4.1, Algebraic Identities, Class 9, Maths Free PDF Download
Importance of RD Sharma Solutions Ex-4.1, Algebraic Identities, Class 9, Maths
RD Sharma Solutions Ex-4.1, Algebraic Identities, Class 9, Maths Notes
RD Sharma Solutions Ex-4.1, Algebraic Identities, Class 9, Maths Class 9 Questions
Study RD Sharma Solutions Ex-4.1, Algebraic Identities, Class 9, Maths on the App
|
© EduRev
|
Education Revolution
|
Follow Us
|
